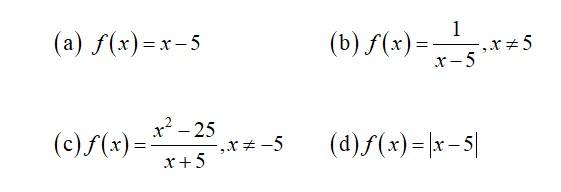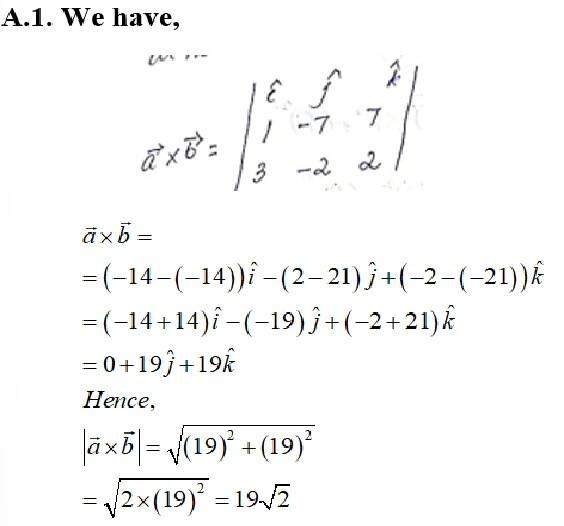Tags Maths

Maths

Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths

Follow Ask Question

6.5k

Questions

Discussions

Active Users

Followers

New answer posted

6 months ago

Maths Continuity and Differentiability

5. Prove that the function $f (x) = x^{n}$ continuous at $x = n,$ where n is a positive integer.

0 Follower 54 Views

alok kumar singh

Contributor-Level 10

4. Given, f (x) = x n > n = positive.

At x = 2,

(x) = n.

$\underset{x \to n}{l i m}$ f (x) = $\underset{x \to n}{l i m}$ x n = n

∴ $\underset{x \to n}{l i m}$ f (x) = f (x)

So f is continuous at x = n.

0 0

New answer posted

6 months ago

Maths Vector Algebra

49. If either $\vec{a}$ = 0 and $\vec{b}$ = 0 then $\vec{a} * \vec{b} = 0$ Is the converse true? Justify your answer with an example.

0 Follower 4 Views

Vishal Baghel

Contributor-Level 10

We take any parallel non- zero vectors so that $\vec{a} * \vec{b} = 0$ .

0 0

New answer posted

6 months ago

Maths Vector Algebra

48. Let the vectors $\vec{a}, \vec{b}, \vec{c}$ be given as $a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k}, b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k}, c_{1} \hat{i} + c_{2} \hat{j} + c_{3} \hat{k}$ then show that $\vec{a} * (\vec{b} + \vec{c}) = \vec{a} * \vec{b} + \vec{a} * \vec{c}$

0 Follower 5 Views

Vishal Baghel

Contributor-Level 10

Given,

$\begin{array}{l} \vec{a} = a_{1} \hat{i} + a_{2} \hat{j} + a_{3} \hat{k} \\ \vec{b} = b_{1} \hat{i} + b_{2} \hat{j} + b_{3} \hat{k} \\ \vec{c} = c_{1} \hat{i} + c_{2} \hat{j} + c_{3} \hat{k} \\ ∴ (\vec{b} + \vec{c}) = (b_{1} + c_{1}) \hat{i} + (b_{2} + c_{2}) \hat{j} + (b_{3} + c_{3}) \hat{k} \\ N o w, \end{array}$

$\begin{array}{l} = \hat{i} {a_{2} (b_{2} + c_{3}) - a_{3} (b_{2} + c_{2})} - \hat{j} {a_{1} (b_{3} + c_{3}) - a_{3} (b_{1} + c_{1})} \\ + \hat{k} {a_{1} (b_{2} + c_{2}) - a_{2} (b_{1} + c_{1})} \\ = \hat{i} {a_{2} b_{2} + a_{2} c_{3} - a_{3} b_{2} - a_{3} c_{2}} - \hat{j} {a_{1} b_{3} + a_{1} c_{3} - a_{3} b_{1} - a_{3} c_{1}} \\ + \hat{k} {a_{1} b_{2} + a_{1} c_{2} - a_{2} b_{1} - a_{2} c_{2}} - - - - (1) \end{array}$

$\begin{array}{l} = \hat{i} (a_{2} b_{3} - a_{3} b_{2}) - \hat{j} (a_{1} b_{3} - a_{3} b_{1}) + \hat{k} (a_{1} b_{2} - a_{2} b_{1}) - - - - (2) \\ A n d, \end{array}$

$\hat{i} (a_{2} c_{3} - a_{3} c_{2}) - \hat{j} (a_{1} c_{3} - a_{3} c_{1}) + \hat{k} (a_{1} c_{2} - a_{2} c_{1}) - - - - (3)$

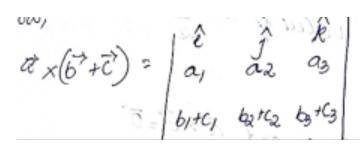
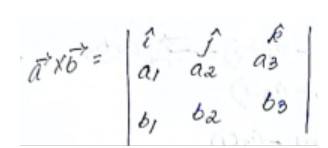
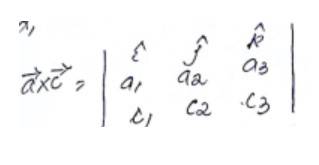
Adding (2) and (3), we get

$\begin{array}{l} (\vec{a} * \vec{b}) + (\vec{a} * \vec{c}) = \hat{i} (a_{2} b_{3} - a_{3} b_{2}) - \hat{j} (a_{1} b_{3} - a_{3} b_{1}) + \hat{k} (a_{1} b_{2} - a_{2} b_{1}) \\ + \hat{i} (a_{2} c_{3} - a_{3} c_{2}) - \hat{j} (a_{1} c_{3} - a_{3} c_{1}) + \hat{k} (a_{1} c_{2} - a_{2} c_{1}) \\ (\vec{a} * \vec{b}) + (\vec{a} * \vec{c}) = \hat{i} (a_{2} b_{3} - a_{3} b_{2} + a_{2} c_{3} - a_{3} c_{2}) + \hat{j} (- a_{1} b_{3} + a_{3} b_{1} - a_{1} c_{3} + a_{3} c_{1}) \\ + \hat{k} (a_{1} b_{2} - a_{2} b_{1} + a_{1} c_{2} - a_{2} c_{1}) \\ = \hat{i} (a_{2} b_{3} + a_{2} c_{3} - a_{3} c_{2} - a_{3} b_{2}) - \hat{j} (a_{1} b_{3} + a_{1} c_{3} - a_{3} b_{1} - a_{3} c_{1}) \\ + \hat{k} (a_{1} b_{2} + a_{1} c_{2} - a_{2} b_{1} - a_{2} c_{1}) - - - - - (4) \end{array}$

From (1) and (4), we have

$\vec{a} (\vec{b} + \vec{c}) = \vec{a} * \vec{b} + \vec{a} * \vec{c}$

Hence, proved.

0 0

New answer posted

6 months ago

Maths Continuity and Differentiability

3. Examine the following functions for continuity.

0 Follower 15 Views

alok kumar singh

Contributor-Level 10

3. (a) Given, f (x) = x 5.

The given f x n is a polynernial f xn and as every pohyouraial f xn is continuous in its domain R we conclude that f (x) is continuous.

(b). Given, f(x) = $\frac{1}{x - 5}, x \neq 5$

For any a $= 3 {(5 x)}^{3 c o s 2 x} [\frac{c o s 2 x}{x} - 2 s i n 2 x l o g 5 x]$ {5},

$= \frac{x^{2} * 1 *}{x - 3} \frac{d}{d x} (x - 3) + l o g (x - 3) \cdot 2 x$ $\frac{1}{(x - 5)} = \frac{1}{a - 5} .$

and f(a) = $\frac{1}{a - 5}$

i e, $f (x) = - (x - 1) + [- (x - 2)] = - x + 1 - x + 2 = 3 - 2 x .$ f(x) = f(a).

Hence f is continuous in its domain.

(c) Given, f(x) = $\frac{x^{2} - 25}{x + 5}, x \neq - 5$

For any a $?$ { 5}

$\underset{x \to a}{l i m} f (x) = \underset{x \to a}{l i m}$ $\frac{x^{2} - 25}{x + 5} = \frac{a^{2} - 25}{a + 5} = \frac{(a - 5) (a + 5)}{a + 5}$ = a 5

And f(a) = $\frac{a^{2} - 25}{a + 5} = \frac{(a - 5) (a + 5)}{a + 5} .$

= a 5

$∴ \underset{x \to a}{l i m}$ f(x) = f(a).

So, f is continuous in its domain.

(d) Given f (a) = $| x - 5 | = {\begin{matrix} x - 5 & , if x - 5 > 0 \Rightarrow x \geq 5 \\ - (x - 5) & if x - 5 < 0 \Rightarrow x < 5 . \end{matrix}$

For x = c < 5.

f (c) = (c 5) = 5 c.

$\underset{x \to c}{l i m}$ f(x) = $\underset{x \to c}{l i m}$ (x 5) = (c 5) = 5 c.

∴ f(c) = $\underset{x \to c}{l i m}$ f(x).

So f is continuous.

For x = c > 5.

f (c) = (x 5) = c 5

$\underset{x \to c}{l i m}$ f(x) = $\underset{x \to c}{l i m}$ (x 5) = c

...more

3. (a) Given, f (x) = x 5.

The given f x n is a polynernial f xn and as every pohyouraial f xn is continuous in its domain R we conclude that f (x) is continuous.

(b). Given, f(x) = $\frac{1}{x - 5}, x \neq 5$

For any a $= 3 {(5 x)}^{3 c o s 2 x} [\frac{c o s 2 x}{x} - 2 s i n 2 x l o g 5 x]$ {5},

$= \frac{x^{2} * 1 *}{x - 3} \frac{d}{d x} (x - 3) + l o g (x - 3) \cdot 2 x$ $\frac{1}{(x - 5)} = \frac{1}{a - 5} .$

and f(a) = $\frac{1}{a - 5}$

i e, $f (x) = - (x - 1) + [- (x - 2)] = - x + 1 - x + 2 = 3 - 2 x .$ f(x) = f(a).

Hence f is continuous in its domain.

(c) Given, f(x) = $\frac{x^{2} - 25}{x + 5}, x \neq - 5$

For any a $?$ { 5}

$\underset{x \to a}{l i m} f (x) = \underset{x \to a}{l i m}$ $\frac{x^{2} - 25}{x + 5} = \frac{a^{2} - 25}{a + 5} = \frac{(a - 5) (a + 5)}{a + 5}$ = a 5

And f(a) = $\frac{a^{2} - 25}{a + 5} = \frac{(a - 5) (a + 5)}{a + 5} .$

= a 5

$∴ \underset{x \to a}{l i m}$ f(x) = f(a).

So, f is continuous in its domain.

(d) Given f (a) = $| x - 5 | = {\begin{matrix} x - 5 & , if x - 5 > 0 \Rightarrow x \geq 5 \\ - (x - 5) & if x - 5 < 0 \Rightarrow x < 5 . \end{matrix}$

For x = c < 5.

f (c) = (c 5) = 5 c.

$\underset{x \to c}{l i m}$ f(x) = $\underset{x \to c}{l i m}$ (x 5) = (c 5) = 5 c.

∴ f(c) = $\underset{x \to c}{l i m}$ f(x).

So f is continuous.

For x = c > 5.

f (c) = (x 5) = c 5

$\underset{x \to c}{l i m}$ f(x) = $\underset{x \to c}{l i m}$ (x 5) = c 5.

∴ f(c) = $\underset{x \to c}{l i m}$ f(x)

So, f is continuous.

For x = c = 5,

f (5) = 5 5 = 0

$\underset{x \to 5^{}}{l i m}$ f(a) = $\underset{x \to 5^{}}{l i m}$ (x 5) = (5 5) = 0

$\underset{x \to 5^{+}}{l i m}$ f(x) = $\underset{x \to 5^{+}}{l i m}$ (x 5) = 5 5 = 0

∴ $\underset{x \to 5^{+}}{}$ + (x) = $\underset{x \to c^{+}}{s i n}$ + (x) = f (c)

Hence f is continuous.

less

0 0

New answer posted

6 months ago

Maths Vector Algebra

47. Given that $\vec{a} . \vec{b} = 0$ and $\vec{a} * \vec{b} = 0$ What can you conclude about the vectors $\vec{a}$ and $\vec{b}$ ?

0 Follower 5 Views

Vishal Baghel

Contributor-Level 10

Given,

$\vec{a} . \vec{b} = 0$ and $\vec{a} * \vec{b} = 0$

For,

$\vec{a} . \vec{b} = 0$ , then either $| \vec{a} | = 0$ or $| \vec{b} | = 0$ or $\vec{a} ⊥ \vec{b}$

For,

$\vec{a} * \vec{b} = 0$ , then either $| \vec{a} | = 0$ or $| \vec{b} | = 0$ or $\vec{a} ? \vec{b}$

$∴$ In case $\vec{a}$ and $\vec{b}$ are non- zero on both side.

But $\vec{a}$ and $\vec{b}$ cannot be both perpendicular and parallel simultaneously.

So, we can conclude that

$| \vec{a} | = 0$ or $| \vec{b} | = 0$

0 0

New answer posted

6 months ago

Maths Vector Algebra

46. Find λ and μ if $(\vec{a} - \vec{b}) * (\vec{a} + \vec{b}) = 2 (\vec{a} * \vec{b})$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

$(2 \hat{i} + 6 \hat{j} + 27 \hat{k}) * (\hat{i} + λ \hat{j} + μ \hat{k}) = \vec{0}$

$\begin{array}{l} \Rightarrow \hat{i} (6 μ - 27 λ) - \hat{j} (2 μ - 27) + \hat{k} (2 λ - 6) \\ = 0 \hat{i} + 0 \hat{j} + 0 \hat{k} \end{array}$

On comparing both side components,

$\begin{array}{l} 6 μ - 27 λ = 0, \\ 2 μ - 27 = 0 \\ 2 μ = 27 \\ μ = \frac{27}{2}, \\ 2 λ - 6 = 0 \\ 2 λ = 6 \\ λ = \frac{6}{2} = 3 \end{array}$

$∴$ Therefore, the value of $μ = \frac{27}{2}$ and $λ = 3$

0 0

New answer posted

6 months ago

Maths Vector Algebra

45. Show that $(\vec{a} - \vec{b}) * (\vec{a} + \vec{b}) = 2 (\vec{a} * \vec{b})$

0 Follower 4 Views

Vishal Baghel

Contributor-Level 10

Show that

$\begin{array}{l} (\vec{a} - \vec{b}) * (\vec{a} + \vec{b}) = 2 (\vec{a} * \vec{b}) \\ (\vec{a} - \vec{b}) * (\vec{a} + \vec{b}) \\ = \vec{a} (\vec{a} + \vec{b}) - \vec{b} (\vec{a} + \vec{b}) \\ = \vec{a} * \vec{a} + \vec{a} * \vec{b} - \vec{b} * \vec{a} - \vec{b} * \vec{b} \\ = 0 + \vec{a} * \vec{b} - \vec{b} * \vec{a} - 0 \\ = \vec{a} * \vec{b} + \vec{a} * \vec{b} [\vec{a} * \vec{b} = - \vec{b} * \vec{a}] \\ = 2 (\vec{a} * \vec{b}) \end{array}$

0 0

New answer posted

6 months ago

Maths Vector Algebra

44. If a unit vector $\vec{a}$ makes an angle π/3 with $\hat{i}, \frac{π}{4} w i t h \hat{j}$ and an acute angle θ with $\hat{k}$ then find θ and hence, the components of $\vec{a}$ .

0 Follower 8 Views

Vishal Baghel

Contributor-Level 10

Let $\vec{a} = (a_{1}, a_{2}, a_{3})$ as component

We know,

$\vec{a}$ is a unit vector, $| \vec{a} | = 1$

Given that,

$\vec{a}$ marks angles $\frac{π}{3}$ with $\hat{i}$ , $\frac{π}{4}$ with $\hat{j}$ and $θ$ with $\hat{k}$ acute angle.

Now,

$c o s \frac{π}{3} = \frac{a_{1}}{| \vec{a} |} \Rightarrow \frac{1}{2} = a_{1} [| \vec{a} | = 1] c o s \frac{π}{4} = \frac{a_{2}}{| \vec{a} |} \Rightarrow1/\sqrt2$
$\begin{array}{l} \frac{}{} = a_{2} \\ c o s θ = \frac{a_{3}}{| \vec{a} |} \Rightarrow a_{3} = c o s θ \end{array}$

We know,

$| \vec{a} | = 1$

0 0

New answer posted

6 months ago

Maths Vector Algebra

43. Find a unit vector perpendicular to each of the vectors $\vec{a} + \vec{b} a n d \vec{a} - \vec{b}, w h e r e \vec{a} = 3 \hat{i} + 2 \hat{j} + 2 \hat{k} a n d \vec{b} = \hat{i} - 2 \hat{j} - 2 \hat{k}$

0 Follower 12 Views

Vishal Baghel

Contributor-Level 10

Given,

$\begin{array}{l} \vec{a} = 3 \hat{i} + 2 \hat{j} + 2 \hat{k} \\ \vec{b} = \hat{i} + 2 \hat{j} - 2 \hat{k} \\ \vec{a} + \vec{b} = 4 \hat{i} + 4 \hat{j}, \vec{a} - \vec{b} = 2 \hat{i} + 4 \hat{j} \end{array}$

A vector which is perpendicular to both $\vec{a} + \vec{b}$ and $\vec{a} - \vec{b}$ is given by

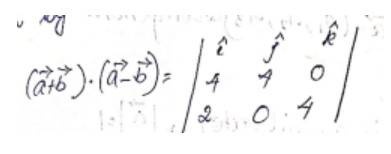
Say

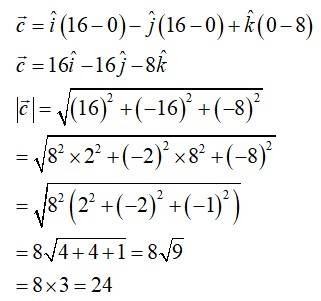
Therefore, the unit vector is

$\begin{array}{l} \frac{\vec{c}}{| \vec{c} |} = \pm \frac{16 \hat{i} - 16 \hat{j} - 8 \hat{k}}{24} \\ = \pm \frac{16}{24} \hat{i} \pm \frac{16}{24} \hat{j} \pm \frac{8}{24} \hat{k} \\ = \pm \frac{2}{3} \hat{i} \pm \frac{2}{3} \hat{j} \pm \frac{1}{3} k \end{array}$

0 0

New answer posted

6 months ago

Maths Vector Algebra

42. Find $| \vec{a} x \vec{b} |$ if $\vec{a} = \hat{i} - 7 \hat{j} = 7 \hat{k}$ and $\vec{b} = 3 \hat{i} - 2 \hat{j} = 2 \hat{k}$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Kindly go through the solution

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
679k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Maths

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience