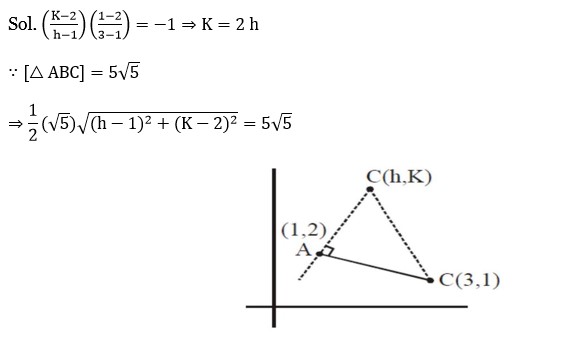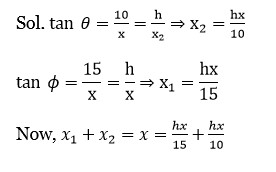Maths
Get insights from 6.5k questions on Maths, answered by students, alumni, and experts. You may also ask and answer any question you like about Maths
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
2 months agoContributor-Level 10
Since (3,3) lies on x²/a² - y²/b² = 1
9/a² - 9/b² = 1
Now, normal at (3,3) is y-3 = -a²/b² (x-3),
which passes through (9,0) ⇒ b² = 2a²
So, e² = 1 + b²/a² = 3
Also, a² = 9/2
(From (i) and (ii)
Thus, (a², e²) = (9/2, 3)
New question posted
2 months agoNew answer posted
2 months agoContributor-Level 10
u = (2z+i)/ (z-ki)
= (2x² + (2y+1) (y-k)/ (x²+ (y-k)²) + I (x (2y+1) - 2x (y-k)/ (x²+ (y-k)²)
Since Re (u) + Im (u) = 1
⇒ 2x² + (2y+1) (y-k) + x (2y+1) - 2x (y-k) = x² + (y-k)²
P (0, y? )
Q (0, y? )
⇒ y² + y - k - k² = 0 {y? + y? = -1, y? = -k-k²}
∴ PQ = 5
⇒ |y? - y? | = 5 ⇒ k² + k - 6 = 0
⇒ k = -3, 2
So, k = 2 (k > 0)
New answer posted
2 months agoContributor-Level 10
Let TV (r) denotes truth value of a statement r.
Now, if TV (p) = TV (q) = T
⇒ TV (S? ) = F
Also, if TV (p) = T and TV (q) = F
⇒ TV (S? ) = T
New answer posted
2 months agoContributor-Level 10
1 + (1 - 2²⋅1) + (1 - 4²⋅3) + . + (1 - 20²⋅19)
= α - 220β
= 11 - (2²⋅1 + 4²⋅3 + . + 20²⋅19)
= 11 - 2² ⋅ Σ? (r=1) r² (2r-1) = 11 - 4 (110²/2) - 35 x 11)
= 11 - 220 (103)
⇒ α = 11, β = 103
New answer posted
2 months agoContributor-Level 10
(a + √2bcosx) (a - √2bcosy) = a² - b²
⇒ a² - √2abcosy + √2abcosx - 2b²cosxcosy = a² - b²
Differentiating both sides:
0 - √2ab (-siny dy/dx) + √2ab (-sinx) - 2b² [cosx (-siny dy/dx) + cosy (-sinx)] = 0
At (π/4, π/4):
ab dy/dx - ab - 2b² (-1/2 dy/dx + 1/2) = 0
⇒ dy/dx = (ab+b²)/ (ab-b²) = (a+b)/ (a-b); a, b > 0
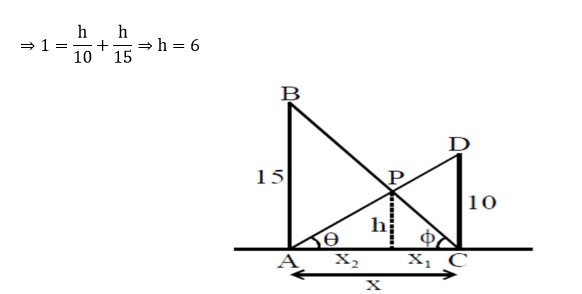
New answer posted
2 months agoContributor-Level 10
f (x) = a? ⋅ (b? * c? ) = |x -2 3; -2 x -1; 7 -2 x|
= x³ - 27x + 26
f' (x) = 3x² - 27 = 0 ⇒ x = ±3 and f' (-3) < 0
⇒ local maxima at x = x? = -3
Thus, a? = -3i? - 2j? + 3k? , b? = 2i? - 3j? - k? , and c? = 7i? - 2j? - 3k?
⇒ a? ⋅ b? + b? ⋅ c? + c? ⋅ a? = 9 - 5 - 26 = -22
New answer posted
2 months agoContributor-Level 10
x? = 10
⇒ x? = (63 + a + b)/8 = 10
⇒ a + b = 17
Since, variance is independent of origin.
So, we subtract 10 from each observation.
So, σ² = 13.5 = (79 + (a-10)² + (b-10)²)/8
⇒ a² + b² - 20 (a+b) = -171
⇒ a² + b² = 169
From (1) and (2) ; a = 12 and b = 5
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers