Ncert Solutions Maths class 11th

89. Let A and d be the first term & common difference of the A.P.

Then,

$ap=a\to A+(p-1)d=a$ ………I

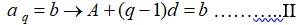
$a_r=c\to A+(M-1)d=c$ …………III

So, L.H.S. $=(q-1)a+(n-p)b+(q-q)c$

$=(q-r)[A+(p-1)d]+(n-p)[A+(q-1)d]+(p-q)[A+(r-1)d]$

{putting value for I, II, III}

$\Rightarrow Aq+q(p-1)d-Ar-r(p-1)d+Ar+r\left(q-1\right)d-Ap-p\left(q-1\right)d$

$+Ap+p\left(r-1\right)d-Aq-q\left(r-1\right)d$

$\Rightarrow pqd-qd-rpd+rd+rqd-rd-pqd+pd+rpd-pd-rqd+qd$

$=0=$ R.H.S

88. Let a and r be the first term & common ratio of the G.P.

So, S = a +ar + ar² +……… upto n terms.

$S=\frac{a\left(1-r^n\right)}{1-r}$

and P = a .ar. ar² ar . upton n terms.

$=a^n{r}^{1+2+3+\dots +(n-1)}$

$=a^{n}r\frac{(n-1)(n-1+1)}{2}$

$=a^{n}r\frac{n(n-1)}{2}$

And R = sum of reciprocal of n terms ( $\frac{1}{a}+\frac{1}{a{r}^n}+...........$ upto n terms)

$=\frac{\frac{1}{a}\left[{\left(\frac{1}{r}\right)}^n-1\right]}{\frac{1}{r}-1}$  As r <1

$\frac{1}{r}$ >1

$=\frac{\frac{1}{a}\left[\frac{1}{r^n}-1\right]}{\frac{1-r}{r}}=\frac{1}{a}\left[\frac{1-r^n}{r^n}\right]*\frac{r}{1-r}$

$=\frac{1-r^n}{a{r}^n}*\frac{r}{1-r}$

$=\frac{1-r^n}{a(1-r)r^{n-1}}$ …. III

Now, L.H.S. = P² Rⁿ

$={\left[a^{n}r\frac{n\left(n-1\right)}{2}\right]}^2·{\left[\frac{1-x^n}{a(1-n)r^{n-1}}\right]}^n$ { equation II & III}

$=a^{2n}\cdot r^{n(n-1)}*\frac{{\left[1-r^n\right]}^n}{a^n(1-n){}^n}{r}^{n(n-1)}$

$=a^{2x-n}*\frac{r^{n(x-1)}}{r^{n(n-1)}}*\frac{{\left[1-x^n\right]}^n}{{(1-r)}^n}$

$=\frac{a^n{\left[1-r^n\right]}^n}{{(1-r)}^n}$

$={\left[\frac{a\left[1-r^n\right]}{(1-r)}\right]}^n$

$=S^n=$R.H.S { $?$ equation I}

87. Here, $\frac{a+bx}{a-bx}=\frac{b+cx}{b-cx}$

$\Rightarrow (a+bx)(b-cx)=(b+cx)(a-bx)$

$\Rightarrow ab-acx+b^{2}x-bc{x}^2=ab-b^{2}x+acx-bc{x}^2$

$\Rightarrow ab-ab-acx-acx=-b^{2}x-b^{2}x+bc{x}^2-bc{x}^2$

$\Rightarrow -2acx=-2b^{2}x$

$\Rightarrow ac=b^2$

$\Rightarrow \frac{c}{b}=\frac{b}{a}$ …………I

And $\frac{b+cx}{b-cx}=\frac{c+dx}{c-dx}$

$\Rightarrow (b+cx)(c-dx)=(c+dx)(b-cx)$

$\Rightarrow bc-bdx+c^{2}x-cdx=bc-c^{2}x+bdx-cdx$

$\Rightarrow bc-bc+c^{2}x+c^{2}x=bdx+bdx-cdx+cdx$ $$

$\Rightarrow 2c^{2}x=2bdx$

$\Rightarrow c^2=bd$

$\Rightarrow \frac{c}{b}=\frac{d}{c}$ ……………II

From I and II

$\frac{a}{a}=\frac{c}{b}=\frac{d}{c}$

a, b, c and d are in G.P.

86. Given, a = 11

Let d and l be the common difference & last term of the A.P.

Then, $a+(a+d)+(a+2d)+(a+3d)=56$ [first 4 terms sum]

$\Rightarrow 4a+6d=56$

$\Rightarrow 6d=56-4a=56-4*11=56-44=12$

$\Rightarrow d=\frac{12}{6}=2$

And, $l+(l-d)+(l-2d)+(l-3d)=112$

$\Rightarrow 4l-6d=112$

$\Rightarrow 4l=112+6d=112+6*2=112+12=124$ [last 4 terms sum]

$\Rightarrow l=\frac{124}{4}=31$

So, $l=31$

$\Rightarrow a+{(n-1)}^d=31$

$\Rightarrow 11+{(n-1)}^2=31$

$\Rightarrow (n-1)2=31-11=20$

$\Rightarrow n-1=\frac{20}{2}=10$

$\Rightarrow n=10+1$

$\Rightarrow n=11$

the A.P. has 11 number of terms.

85. Let a and r be the first term and common ratio of G.P.

Then, number of term = 2n (even).

$a_1+a_2+?+a_{2n}=5\left(a_1+a_3+?+a_{2n-1}\right)[?]$

$\Rightarrow a+ar+.........+a{r}^{2n-1}=5\left(a+a{r}^2+.......+a{r}^{2n-1-1}\right)$

$\Rightarrow \frac{a\left(1-r^{2n}\right)}{1-n}=5*\frac{a\left[1-{\left(r^2\right)}^n\right]}{1-r^2}$ { series on R.H.S. has $\frac{2n}{2}=n$ terms and common ratio $\frac{a{r}^2}{a}=r^2$ }

$\Rightarrow \frac{1-r^{2n}}{1-r}=\frac{5\left[1-r^{2n}\right]}{1-r^2}$ (eliminating a)

$\Rightarrow \frac{1-r^{2r}}{1-r}=\left[\frac{1-r^{2r}}{1-r}\right]*\frac{5}{1+r}\left\{?a^2-b^2=(a-b)(a+b)\right\}$ 

$1=\frac{5}{1+r}\{Eliminating\; same\; term\}$

$\Rightarrow 1+r=5$

$\Rightarrow r=5-1$

r = 4

84. Let a, ar and $a{r}^2$ be the three nos. which is in G.P.

Then, a + ar + ar² = 56

a ( 1 + r + r²) =56  -I

Given, that a1, ar 7, ar² - 21 from an AP we have,

$(ar-7)-(a-1)=\left(a{r}^2-21\right)-(ar-7)$

$\Rightarrow ar-7-a+1=a{r}^2-21-ar+7$

$\Rightarrow ar-a-6=a{r}^2-ar-14$

$\Rightarrow a{r}^2-ar-ar+a-a-14-6$

$\Rightarrow a{r}^2-2ar+a=8$

$\Rightarrow a\left(r^2-2r+1\right)=8$ ………………. II

Now, dividing equation I by II we get,

$\Rightarrow \frac{a\left(1+n+n^2\right)}{a\left(r^2-2r+1\right)}=\frac{56}{8}$

$\Rightarrow 1+r+r^2=7\left(n^2-2n+1\right)$

$\Rightarrow 1+r+r^2=7r^2-14n+7$

$\Rightarrow 7r^2-14n+7-1-x-r^2=0$

$\Rightarrow 6r^2-15r+6=0$

$\Rightarrow 2r^2-5r+2=0$ (dividing by 3 throughout)

$\Rightarrow 2r^2-4r-r+2=0$

$\Rightarrow 2r(r-2)-(r-2)=0$

$\Rightarrow (r-2)(2r-1)=0$

$\Rightarrow r-2=02r-1=0$

$\Rightarrow r=2r=\frac{1}{2}$

So, when r = 2, putting in equation I,

$\Rightarrow a\left(1+2+2^2\right)=56$

$\Rightarrow a(1+2+4)=56$

$\Rightarrow a(7)=56$

$\Rightarrow a=\frac{56}{7}=8$

The numbers are 8, 8* 2, 8* 2² = 8, 16, 32.

And When $r=\frac{1}{2}$ putting in equation I,

$a\left(1+\frac{1}{2}+\frac{1}{2^2}\right)=56$

$\Rightarrow a\left(1+\frac{1}{2}+\frac{1}{4}\right)=56$

$\Rightarrow a\left(\frac{4+2+1}{4}\right)=56$

$\Rightarrow a*\frac{7}{4}=56$

$\Rightarrow a=56*\frac{4}{7}=32$

So, the numbers are $32,32*\frac{1}{2},32*{\left(\frac{1}{2}\right)}^2\Rightarrow 32,16,8$

83. Given, a = 1

$a_3+a_5=90$

Let r be the common ratio of the G.P.

So,

Let r be the common ratio of the G.P.

So,

$a_3+a_5=a{r}^{3?1}+a{r}^{5?1}=90$

$?a\left[r^2+r^4\right]=90$

$?1\left[r^2+r^4\right]=90\text{?}\{?a=1\}$

$?r^4+r^2?90=0$

Let $x=r^2$ so we can write above equation as

$x^2+x?90=0x=r^2$

82. Given, a = 5

$r=2>1$

$s_n=315$

So,  $\frac{a\left(r^n-1\right)}{r-1}=315$

$\Rightarrow \frac{5\left(2^n-1\right)}{2-1}=315$

$\Rightarrow 2^n-1=\frac{315}{5}$

$\Rightarrow 2^n=63+1$

$\Rightarrow 2^n=64=26$

$\therefore n=6$

Hence, last term $=a_6=a{r}^{6-1}=a{r}^5=5*2^5=5*32$

= 160

81. Given, $f(x+y)=f(x)\cdot f(y).Ux,y\in N$ and $f\left(1\right)=3$

Putting (x, y) = (1+1) we get

Putting (x, y) = (1,1) we get,

$f(1+1)=f(1)\cdot f(1)=3\cdot 3=9$

$\Rightarrow f(2)=9$

And putting $(x,y)=(1,2)$ we get,

$f(1+2)=f(1)\cdot f(2)=3*9=27$

$f(3)=27$

$f(1)+f(2)+f(3)+?+f(x)={\displaystyle \sum _{x=1}^{n}f}(x)=120$ (Given)

As, With a = 3

$r=\frac{9}{3}=3>1$

We can write equation I as ,

$\frac{a\left(r^n-1\right)}{r-1}=120$

$\Rightarrow \frac{3\left(3^n-1\right)}{3-1}=120$

$\frac{3}{2}\left(3^n-1\right)=120$

$\Rightarrow \left(3^n-1\right)=120*\frac{2}{3}$

3ⁿ 1 = 80

3ⁿ = 81 +1

3ⁿ = 81

3ⁿ = 3⁴

n = 4

80. Two digits no. when divided by 4 yields 1 as remainder are, 12+1, 16+1, 20+1 …., 96+1

13, 17, 21, ………97 which forms an A.P.

So, a = 13

$d=17-13=4$

$l=97$

$\Rightarrow a+(x-1)d=97$

$\Rightarrow 13+(x-1)4=97$

$\Rightarrow \left(x-1\right)4=97-13=84$

$\Rightarrow x-1=\frac{84}{4}=21$

$\Rightarrow x=21+1=22$

Sum of numbers in A.P. = $\frac{x}{2}(a+l)$

$=\frac{22}{2}(13+97)$

= 11* 110

= 1210