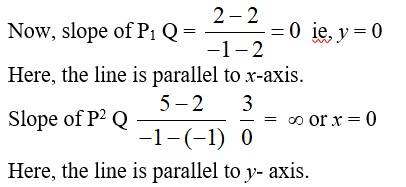Ncert Solutions Maths class 11th
Get insights from 1.6k questions on Ncert Solutions Maths class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
3. On tossing a coin the possible outcomes are Head and Tail. The sample space of tossing a coin four times is
S = {HHHH, THHH, HTHH, HHTH, HHHT, TTTT, HTTT, THTT, TTHT, TTTH, TTHH, HHTT, THTH, HTHT, THHT, HTTH}
New answer posted
4 months agoContributor-Level 10
2. When a dice is thrown, we have 36 the possible outcome.
Dice 2 Dice 1 | 1 | 2 | 3 | 4 | 5 | 6 |
1 | (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) |
2 | (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
3 | (3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) | (3, 6) |
4 | (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
5 | (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
6 | (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
New answer posted
4 months agoContributor-Level 10
1. On tossing a coin the possible outcomes are that of a head or a tail. So, the angle space of tossing a coin three times is
S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
New answer posted
4 months agoContributor-Level 10
76.
If point P be the junction between the lines
2x – 3y + 4 = 0 ______ (1)
3x + 4y – 5 = 0 ______ (2)
Solving (1) and (2) using 3 * (1) – 2 * (2) we get,
6x – 9y + 12 – (6x + 8y – 10) = 0
–17y + 22 = 0
y =
And 2x = 3y– 4
=> 2x = 3 * – 4
x = – 2 = =
Hence, the co-ordinate of the junction is P
The eqn of the path to be reach is
6x – 7y + 8 = 0 _____ (3)
Then, least distance will be perpendicular path.
So, slope of ⊥ path =
Hence eqn of shortest/least distance path from P is
119x + 102y – 125 = 0
New answer posted
4 months agoContributor-Level 10
Let A have the co-ordinate (x, o)
By laws of reflection
∠PAB = ∠ QAB = θ
And ∠ CAQ + θ = 90°
As normal is ⊥ to surface (x-axis)
⇒ ∠CAQ = 90° - θ
and ∠CAP = 90° + θ
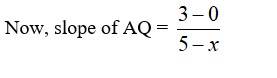
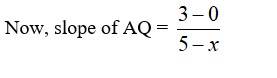

New answer posted
4 months agoContributor-Level 10
73. The given eqn of limes are.
9x + 6y – 7 = 0 ______ (1)
3x + 2y + b = 0 ______ (2)
Let P (x0, y0) be a point equidistant from (1) and (2) so
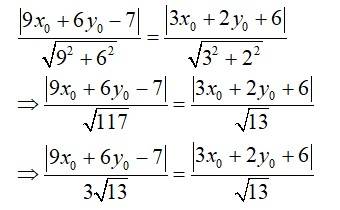
9x0 + 6y - 7 = ± 3 (3x0 + 2y0 + 6)
When, 9x0 + 6y0 – 7 = 3 (3x0 + 2y0 + 6)
⇒ 9x0 + 6y0 - 7 = 9x0 + 6y0 + 18
⇒ - 7 = 18 which in not true
So, 9x0 + 6y0 - 7 = -3 (3x0 + 2y0 + 6)
⇒ 9x0 + 6y0 -7 = -9x0 -6y0 -18
⇒ 18x0 + 12y0 + 11= 0.
Hence, the required eqn of line through (x0, y0) & equidistant from parallel line 9x + 6y - 7 = 0
and 3x + 2y + 6 = 0 is 18x + 12y + 11 = 0.
New answer posted
4 months agoContributor-Level 10
72. The given eqn of the lines are.
x + y ? 5 = 0 _______ (1)
3x ? 2y + 7 = 0 ______ (2)
Given, sum of perpendicular distance of P (x, y) from the two lines is always 10 .
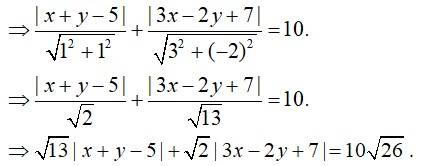
The above eqn can be expressed as a linear combination Ax + By + C = 0 where A, B & C are constants representing a straight line
P (x, y) mover on a line.
New answer posted
4 months agoContributor-Level 10
70. The given equation of the line is
l1: x + y = 4
Let P (x0, y0) be the point of intersect of l1 and the line to be drawn.
Then, x0 + y0 = 4 ⇒ y0 = 4? x
Given, distance between P (x0, y0) and Q (? 1, 2) is 3
ie, ![]()
⇒ (x0 + 1)2 + (y? 2)2= 9
⇒x20+1+ 2x0 + (4? x? 2)2 = 9
⇒ x20+ 2x0 + 1 + (2? x0 )2 = 9
⇒x20+ 2x0 + 1 + 4 + x20 ? 4x0 ?9 = 0
⇒ 2 x20 ?2x0 ? 4 = 0
x20 ? x0 ? 2 = 0
x20 + x0 ? 2x0 ? 2 = 0
x0 (x +1)? 2 (x0 +1) = 0
(x0 +1) (x0 ? 2) = 0
x0 = 2 and x0 =? 1
When, x0 = 2, y0 = 4 ?2 = 2.
and when x0 =? 1, y0 = y? (?1) =5.
The points of interaction of line l1which are at distance 3 unit
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers