Ncert Solutions Maths class 11th
Get insights from 1.6k questions on Ncert Solutions Maths class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
36. Given, A={9,10,11,12,13}.
f(x)=the highest prime factor of n.
and f: A → N.
Then, f(9)=3 [? prime factor of 9=3]
f (10)=5 [? prime factor of 10=2,5]
f(11)=11 [? prime factor of 11 = 11]
f(12)=3 [? prime factor of 12 = 2, 3]
f(13)=13 [? prime factor of 13 = 13]
?Range of f=set of all image of f(x) = {3,5,11,13}.
New answer posted
4 months agoContributor-Level 10
35. Given, f={(ab, a+b): a, b z}
Let a=1 and b=1; a, b z.
So, ab=1 * 1=1
a+b=1+1=2.
So, we have the order pair (1,2).
Now, let a= –1 and b= –1; a, b z
So, ab=(–1) * (–1)=1
a+b=(–1)+(–1)= –2
So, the ordered pair is (1, –2).
?The element 1 has two image i.e., 2 and –2.
Hence, f is not a function.
New answer posted
4 months agoContributor-Level 10
34. Given,
A={1,2,3,4}
B={1,5,9,11,15,16}
f={(1,5),(2,9),(3,1),(4,5),(2,11)}.
(i) As every element of f is an element of A * B
We can clearly say that f A * B.
?f is a relation from A to B.
(ii) As the element 2 of the domain has two image i.e., 9 and 11. f is not a function.
New answer posted
4 months agoContributor-Level 10
69.
The given eqn of the lines are.
4x + 7y + 5 = 0______ (1)
2x - y = 0 ______ (2)
Solving (1) and (2) we get,
4 x + 7 (2 x)+5 = 0
4x +14 x + 5= 0
x =
and y = 2x =
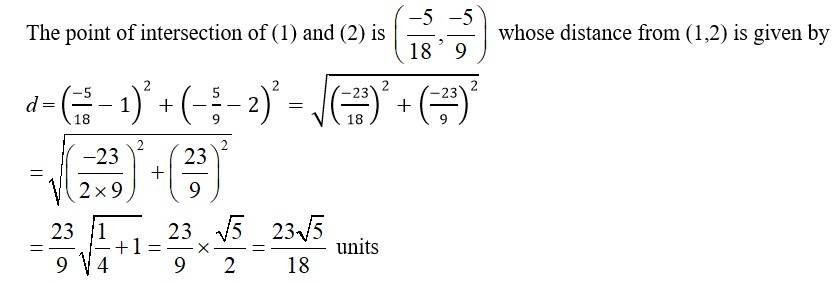
New answer posted
4 months agoContributor-Level 10
33. Given, R= { (a, b): a, b N and a = b2}
(i) Let a = 2 N
Then b = 22 = 4 N
but a ≠ b.
Hence the given statement is not true.
(ii) For a=b2 the inverse b=a2 may not hold true
Example (4,2) R, a=4, b=2 and a=b2
but (2,4) R.
Hence, the given statement is not true.
(iii) If (a, b) R
a=b2…… (1)
and (b, c) R
b=c2……. (2)
so for (1) and (2),
a= (c2)2=c4.
is, a ≠c2,
Hence, (a, c) R.
? The given statement is false.
New answer posted
4 months agoContributor-Level 10
32. Given, f(x) = (ax + b)
= {(1,1),(2,3),(0, – 1),(–1, –3)} .
As (1,1) f.
Then, f(1)=1 [? f(x) = y for (x, y)]
a * 1+b=1
a+b=1…… (1)
and (0, – 1) f .
Then, f(0)= –1
a* 0+b= –1
b= –1…….(2)
Putting value of (2) in (1) we gets
a – 1=1
a=1+1
a=2
So, (a, b)=(2, –1)
New answer posted
4 months agoContributor-Level 10
31. Given, f(x) = x+1. and g(x) = 2x – 3.
So, (f +g)(x) = f(x)+g(x) = (x+1)+(2x – 3) = x+1+2x – 3 = 3x – 2
(f – g)(x) = f(x) –g(x) = (x+1)–(2x–3) = x+1 – 2x+3 = 4 – x
New answer posted
4 months agoContributor-Level 10
68. The given eqn of line is
l1: x + y = 4
Let R divides the line joining two points P (?1,1) and Q (5,7) in ratio k:1. Then,
Co-ordinate of R = ()
As l1 divides line joining PQ, then R lies on l1
i e, =4
5k ?1 + 7k + 1= 4 (k + 1)
12k = 4k + 4
8k = 4
k =
The ratio in which x + y = 4 divides line joining (?1,1) ad (5,7) is :1 i.e., 1: 2.
New answer posted
4 months agoContributor-Level 10
30. Given, f (x)=
We know that, for x R.
So, x2≥ 0 ⇒
and x2+1>x2
⇒
⇒1 > f (x).
So, 0 ≤ f (x) < 1
∴ Range of f (x) = [0,1).
New answer posted
4 months agoContributor-Level 10
67. The given eqn of line is.
l1 : y = mx + c.
Slope of l1 = m
Let m? be the slope of line passing through origin (0, 0) and making angle θ with l1
Thus, (y 0) = m? (x 0)
y = m? x
m? =
______ (1)
And tanθ = =
When, tanθ =
tanθ + m? m tanθ = m' - m
m + tanθ = m? - m?m tanθ
m' =
When tan θ =
tan θ + m? m tanθ = -m? + m
m' =
Hence combining the two we get,
{-: eqn (1) }
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers
