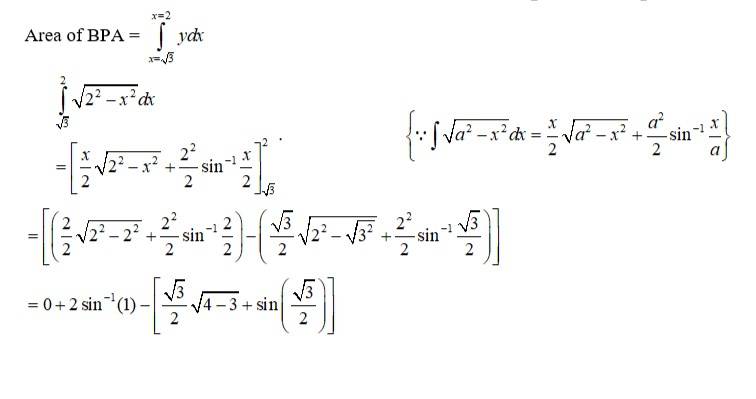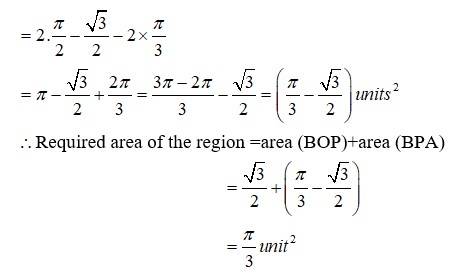Ncert Solutions Maths class 12th
Get insights from 2.5k questions on Ncert Solutions Maths class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Ncert Solutions Maths class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
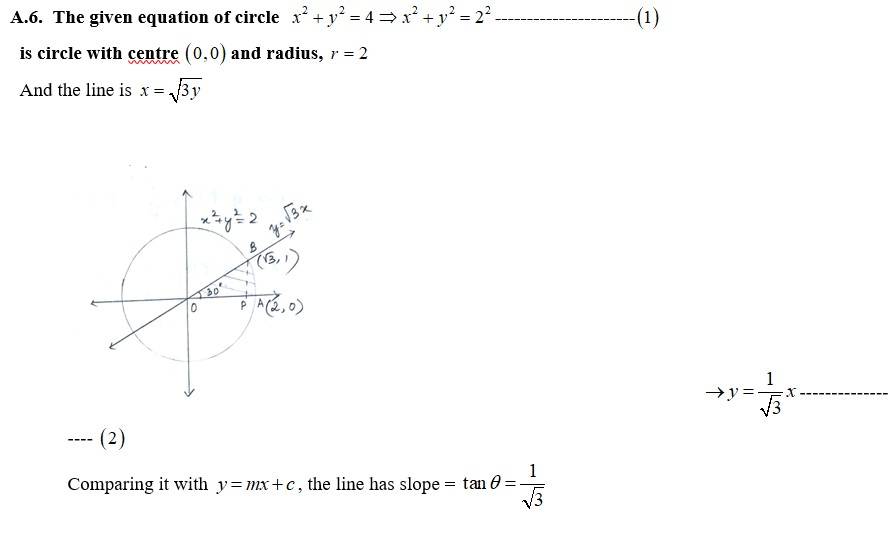
The equation given circle is
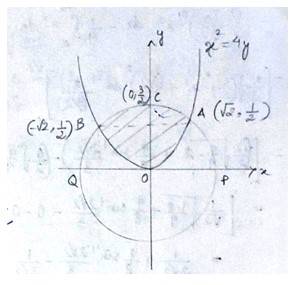
i.e, centre (0,0), radius
since intersect the circle
we can put in
which is not possible or cannot be (-)ve


New answer posted
4 months agoContributor-Level 10
As intersect at Athen,
A has coordinate
Hence, area of curve =
Option (B) is correct
New answer posted
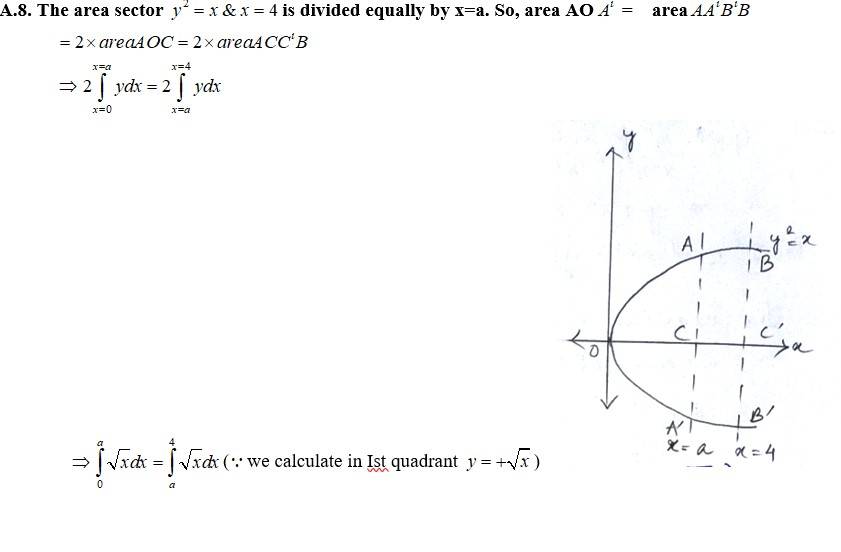
4 months agoContributor-Level 10
The given equation of the curve is
in Ist quadrant
So, area of curve enclosed by
And area (AOCA)
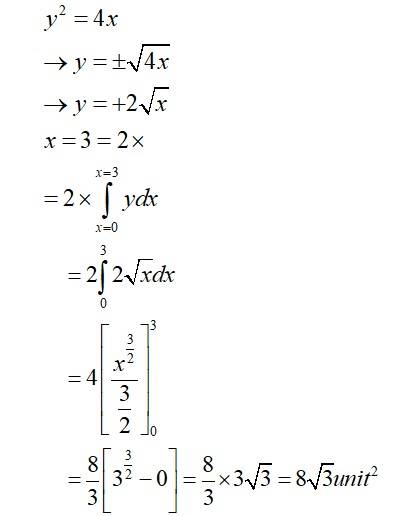
New answer posted
4 months agoContributor-Level 10
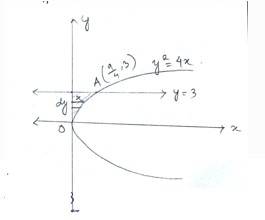
Given curve is and the equation of line is
The point of intersection of the curve and the line can be determine as follows.
Put,
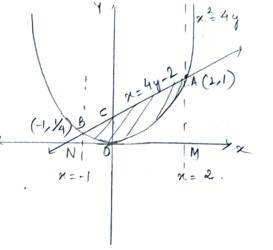
In to determine value of x
i.e,
and
, we have
And at we have
So, the coordinates A and B are (2,1) and ( )
The required area before the line & the curve is area = area of trapezium (BNMAB)- area under curve BDA
New answer posted
4 months agoContributor-Level 10
Given that equation of
curve
line
Since the line passes through A&B in Ist and IInd quadrants
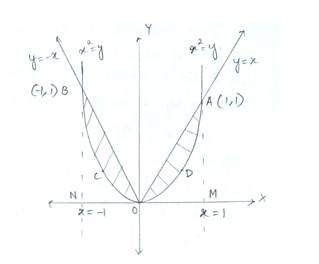
the equation must satisfy
for Ist quadrant and
for IInd t quadrant
So, and
and
i.e, A has coordinate (1,1)
i.e, B has coordinate (1,1)
Now, area of AODA = area (AOM)-area (ADOM)
The required area of the region bounded by curve and line is
New answer posted
4 months agoContributor-Level 10
Kindly go through the solution
(Squaring both sides)
(Taking cube on both sides)
New question posted
4 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 687k Reviews
- 1800k Answers