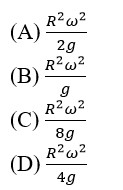Overview

The maximum and minimum distances of a comet from the Sun are 1.6 x1012m and 8.0 x1010m respectively. If the speed of the comet at the nearest point is 6x104ms-1, the speed at the farthest point is:

0 Follower 1 View

Raj Pandey

Contributor-Level 9

Kindly consider the following Image

0 0

New answer posted

a month ago

Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is:

0 Follower 2 Views

Contributor-Level 10

F = Gm²/ (2R)² = mω²R Given m = 1kg
⇒ ω² = Gm/ (4R³)
⇒ ω = (1/2)√ (G/R³)

0 0

New answer posted

a month ago

The planet Mars has two moons, if one of them has a period 7 hours, 30 minutes and an orbital radius of 9.0 * 10³ km. Find the mass of Mars.
{Given 4π²/G = 6 * 10¹¹ N⁻²kg²}

0 Follower 3 Views

Contributor-Level 10

T² = (4π²r³)/GM
⇒ M = (4π²r³)/ (G T²)
⇒ M = 6 * 10¹¹ * (9 * 10? )³ / (450 * 60)²
= 6.48 x 10²³ kg
(Note: There is a calculation error in the source image. Using the formula and given values: M = (6e11 * (9e6)^3) / (27000)^2 = 6e23 kg)

0 0

New answer posted

a month ago

Suppose two planets (spherical in shape) of radii R and 2R, but mass M and 9M respectively have a centre to centre separation 8R as shown in the figure. A satellite of mass 'm' is projected from the surface of the planet of mass 'M' directly towards the centre of the second planet. The minimum speed 'v' required for the satellite to reach the surface of the second planet is √(aGM/(7R)) then the value of 'a' is _______. [Given: The two planets are fixed in their position]

0 Follower 2 Views

Contributor-Level 10

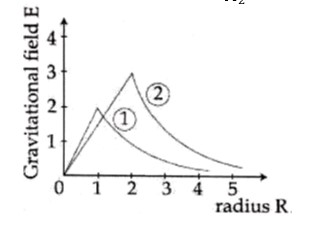
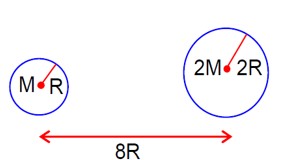
We have to find the point where the gravitational field must be zero.
EG = 0
GM/x² = G (9M)/ (8R-x)²
1/x² = 9/ (8R-x)²
8R - x = 3x => x = 2R
Potential at A (surface of first planet), VA = -GM/R - G (9M)/7R = -16GM/7R
Potential at point x, Vx = -GM/x - G (9M)/ (8R-x) = -GM/2R - G (9M)/6R = -2GM/R
ΔV = Vx - VA = -2GM/R - (-16GM/7R) = (-14+16)GM/7R = 2GM/7R
Using conservation of mechanical energy
ΔKE = ΔU = mΔV
½mv² = m (2GM/7R)
v² = 4GM/7R
v = √ (4GM/7R) => a = 4

0 0

New answer posted

a month ago

Consider a planet in some solar system which has a mass double the mass of earth and density equal to the average density of earth. If the weight of an object on earth is W, the weight of the same object on that planet will be :

0 Follower 2 Views

Contributor-Level 10

g = (4/3)πRρG . (i) (ρ = density)
Now ρ = M/V = M/ (4/3)πR³)
R³ = M/ (4/3)πρ) => R ∝ (M/ρ)¹/³
From equation (i)
g ∝ Rρ ∝ (M/ρ)¹/³ρ = M¹/³ρ²/³
For planet, M' = 2M, ρ' = ρ
g'/g = (M'/M)¹/³ (ρ'/ρ)²/³ = (2)¹/³ (1)²/³ = 2¹/³
W' = mg' = m (2¹/³g) = 2¹/³ (mg) = 2¹/³W

0 0

New answer posted

a month ago

Two stars of masses m and 2m at a distance d rotate about their common centre of mass in free space. The

0 Follower 4 Views

Contributor-Level 10

$m ω^{2} . \frac{2 d}{3} = \frac{G . m . 2 m}{d^{2}} \Rightarrow ω = \sqrt[]{\frac{3 G m}{d^{3}}}$

$T = \frac{2 π}{ω} = 2 π \sqrt[]{\frac{d^{3}}{3 G m}}$

0 0

New answer posted

a month ago

Four identical particles of equal masses 1kg made to move along the circumference of a circle of radius 1m under the actin of their own mutual gravitational attraction. The speed of each particle will be:

0 Follower 2 Views

Contributor-Level 10

$F_{1} c o s 45 ° + F_{2} c o s 45 ° + F_{3} = \frac{m v^{2}}{r}$

$\Rightarrow \frac{G m^{2}}{{(\sqrt[]{2} r)}^{2}} . \frac{1}{\sqrt[]{2}} + \frac{G m^{2}}{{(\sqrt[]{2} r)}^{2}} . \frac{1}{\sqrt[]{2}} + \frac{G m^{2}}{{(2 r)}^{2}} = \frac{m v^{2}}{r}$

$\Rightarrow v = \sqrt[]{\frac{G m}{4 r} (2 \sqrt[]{2} + 1)}$

Putting m = 1 kg and r = 1 m,

$v = \frac{1}{2} \sqrt[]{G (1 + 2 \sqrt[]{2})}$

0 0

New answer posted

a month ago

Consider two satellites S₁ and S₂ with periods of revolution 1hr. and 8 hr. respectively revolving around a planet in circular orbits. The ratio of angular velocity of satellite S₁ to the angular velocity of satellites S₂ is:

0 Follower 2 Views

Contributor-Level 10

$ω = \frac{2 π}{T} \Rightarrow \frac{ω_{1}}{ω_{2}} = \frac{T_{2}}{T_{1}} = 8$

0 0

New answer posted

a month ago

In the reported figure of earth, the value of acceleration due to gravity is same at point A and C but it is smaller than that of its value at point B (surface of the earth). The value of OA: AB will be x : y. The value of x is…………

0 Follower 2 Views

Contributor-Level 10

$\frac{G M}{{(3 R / 2)}^{2}} = \frac{G M}{R^{3}} * r$

$\Rightarrow O A = \frac{4 R}{9} = r$

$A B = R - \frac{4 R}{9} = \frac{5 R}{9} \Rightarrow O A : A B = 4 : 5 = x : y \Rightarrow x = 4$

0 0

New answer posted

a month ago