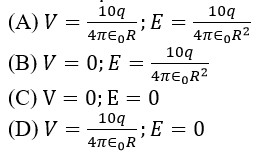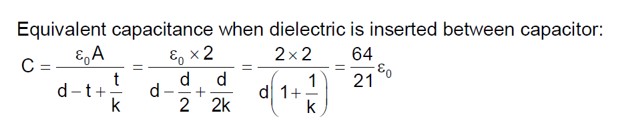Physics Electrostatic Potential and Capacitance
Get insights from 132 questions on Physics Electrostatic Potential and Capacitance, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Electrostatic Potential and Capacitance
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
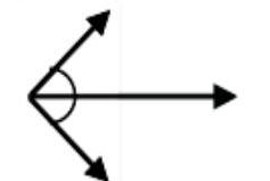
Potential of centre, = V =
Vc = K (Σq)/R
Vc = K (0)/R = 0
Electric field at centre E_B = E_B = ΣE
Let E be electric field produced by each
charge at the centre, then resultant electric field will be
Ec = 0, since equal electric field vectors are acting at equal angle so their resultant is equal to zero.
New answer posted
4 months agoContributor-Level 10
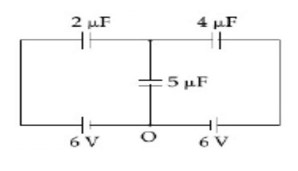
Now, using junction analysis
We can say, q? + q? + q? = 0
2 (x - 6) + 4 (x - 6) + 5 (x) = 0
x = 36/11, q? = 36 (5)/11 = 180/11
q? = 16.36µC
New answer posted
4 months agoContributor-Level 10
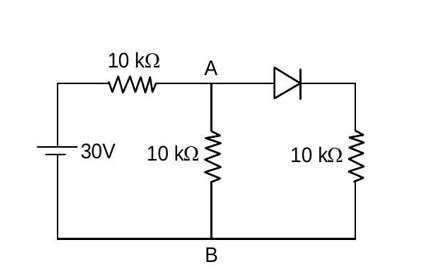
In forward bias diode act as a short circuit wire. Hence, the equivalent circuit is now.
New answer posted
4 months agoContributor-Level 10
As charge remains same. So,
Initial total charge Q = (2C)V + CV = 3CV
When dielectric is inserted in C, its new capacitance is KC.
The capacitors 2C and KC are in parallel.
Equivalent capacitance C_eq = 2C + KC = (K+2)C
New potential Vc = Q/C_eq = 3CV/ (K+2)C) = 3V/ (K+2)
New answer posted
4 months agoContributor-Level 10
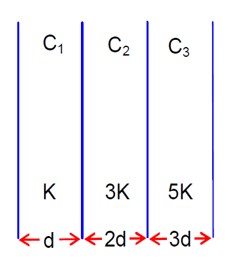
1/Ceq = 1/C? + 1/C? + 1/C?
1/Ceq = 1/ (K Aε? /d) + 1/ (3K Aε? /2d) + 1/ (5K Aε? /3d)
1/Ceq = d/ (K Aε? ) + 2d/ (3K Aε? ) + 3d/ (5K Aε? )
1/Ceq = (d/K Aε? ) * (1 + 2/3 + 3/5)
1/Ceq = (d/K Aε? ) * (15+10+9)/15) = 34d / (15K Aε? )
Ceq = 15K Aε? / 34d
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers