Tags Physics Electrostatic Potential and Capacitance

Physics Electrostatic Potential and Capacitance

Get insights from 131 questions on Physics Electrostatic Potential and Capacitance, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Electrostatic Potential and Capacitance

Follow Ask Question

131

Questions

Discussions

Active Users

Followers

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

If qf is the free charge on the capacitor plates and qb is the bound charge on the dielectric slab of dielectric constant k placed between the capacitor plates, then bound charge qb can be expressed as:

0 Follower 23 Views

alok kumar singh

Contributor-Level 10

Enet = Eo/k
Enet = E_free - E_bound = qf/Aε? - qb/Aε?
Eo = qf/Aε?
So, (qf-qb)/Aε? = qf/ (kAε? )
qf - qb = qf/k
qb = qf (1 - 1/k)

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is:

0 Follower 8 Views

alok kumar singh

Contributor-Level 10

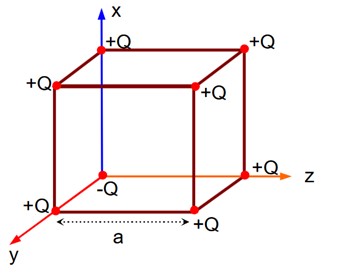
If charge (-Q) at origin is replaced by (+Q), then electric field at the centre of the cube is zero. Thus, electric field at the centre of the cube is as if only (-2Q) charge is present at the origin.

$\vec{E} = \frac{1}{4 π ε_{0}} \frac{(- 2 Q)}{{(\frac{\sqrt[]{3}}{2} a)}^{2}} . \frac{1}{\sqrt[]{3}} (\hat{x} + \hat{y} + \hat{z}) = \frac{| - 2 Q}{3 \sqrt[]{3} π ε_{0} a^{2}} (\hat{x} + \hat{y} + \hat{z})$

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

Two equal capacitors are first connected in series and then in parallel. The ratio of the equivalent capacities in

0 Follower 1 View

alok kumar singh

Contributor-Level 10

When connected in series, equivalent capacitance,

$C_{1} = \frac{C * C}{C + C} = \frac{C}{2}$

When connected in parallel, equivalent capacitance

C₂ = C + C = 2C

$\frac{C_{1}}{C_{2}} = \frac{C / 2}{2 C} = \frac{1}{4}$

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

If 'C' and 'V' represent capacity and voltage respectively then what are the dimensions of $λ$ where C/V = $λ$

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

$λ = \frac{c}{v} = \frac{Q^{3}}{W^{2}} = \frac{I^{3} T^{3}}{M^{2} L^{4} T^{- 4}} \Rightarrow [λ] = [M^{- 2} L^{- 4} T^{7} l^{3}]$

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

Consider the combination of 2 capacitors C₁ and C₂, with C₂ > C₁, when connected in parallel, the equivalent capacitance is $\frac{15}{4}$ times the equivalent capacitance of the same connected in series, Calculate the ratio of capacitors, $\frac{C_{2}}{C_{1}} .$

0 Follower 3 Views

Payal Gupta

Contributor-Level 10

According question, we can write

$\frac{C_{1} * C_{2}}{C_{1} + C_{2}} = \frac{15}{4} (C_{1} + C_{2}) \Rightarrow 4 C_{1} C_{2} = 15 (C_{1}^{2} + C_{2}^{2} + 2 C_{1} C_{2})$

$\Rightarrow 4 (\frac{C_{2}}{C_{1}}) = 15 {(\frac{C_{2}}{C_{1}})}^{2} + 30 (\frac{C_{2}}{C_{1}}) + 15 \Rightarrow 15 x^{2} + 26 x + 15 = 0,$ where x = $\frac{C_{2}}{C_{1}}$

$\Rightarrow x = \frac{- 26 \pm \sqrt[]{676 - 900}}{30}$

Since x cannot be real, so this Question has been dropped by NTA

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

Two identical conducting spheres with negligible volume have 2.1 nC and 0.1 nC charges, respectively. They are brought into contact and then separated by a distance of 0.5m. The electrostatic force acting between the spheres is …………….* 10^-9N.

$[G i v e n : 4 π ε_{0} = \frac{1}{9 * 1 0^{9}} S I u n i t]$

0 Follower 4 Views

Payal Gupta

Contributor-Level 10

After contact, charges an each sphere will be

$\frac{q_{1} + q_{2}}{2} = 1 n c \Rightarrow F = \frac{k q_{1} q_{2}}{r^{2}} = 36 * 1 0^{- 9} N$

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

Two small spheres each of mass 10mg are suspended from a point by threads 0.5m long. They are equally charged and repel each other to a distance of 0.20m. The charge on each of the sphere is $\frac{a}{21} * 1 0^{- 8} C .$ The value of 'a' will be……. [Given g = 10 ms^-2]

0 Follower 5 Views

Payal Gupta

Contributor-Level 10

$T s i n θ = \frac{k q^{2}}{r^{2}}$

$T c o s θ = m g$

$t a n θ = \frac{k q^{2}}{m g r^{2}}$

Using the above equation find the value of 'q'

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

If the plates of a parallel plate capacitor connected to a battery are moved close to each other, then

A. the charge stored in it, increases.

B. the energy stored in it, decreases.

C. its capacitance increases.

D. the ratio of charge to its potential remains the same.

E. the product of charge and voltage increases.

Choose the most appropriate answer from the options given below:

0 Follower 6 Views

alok kumar singh

Contributor-Level 10

Given $V^{'} = V =$ Constant

(i) $C^{'} = \frac{ε_{0} A}{d^{'}}, C = \frac{ε_{0} A}{d}$

$d^{'} < d$

$C^{'} > C$
Hence, final capacitance greater than initial capacitance,

(ii) $U^{'} = \frac{1}{2} C^{'} V^{2}$

$U = \frac{1}{2} C V^{2}$

$U^{'} > U$

Hence final energy is greater than initial energy

(iii) $\frac{Q^{'}}{V^{'}} = C^{'}$ and $\frac{Q}{V} = C$

$\frac{Q^{'}}{V^{'}} \neq \frac{Q}{V}$

(iv) Product of charge and voltage

$X^{'} = Q^{'} V = C^{'} V^{2}$

$X = Q V = C V^{2}$

$X^{'} > X$

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

A thin spherical shell is charged by some source. The potential difference between the two points $C$ and $P$ (in V) shown in the figure is:

(Take $\frac{1}{4 π ε_{0}} = 9 * 1 0^{9}$ SI units)

0 Follower 5 Views

alok kumar singh

Contributor-Level 10

For uniformly charged spherical shell,

$V = \frac{k q}{R} (For r \leq R)$

$∴ V_{C} = V_{P}$

$V_{C} - V_{P} = Zero$

0 0

New answer posted

6 months ago

Physics Electrostatic Potential and Capacitance Class 12th

If $c$ is the velocity of light in free space, the correct statements about photon among the following are:

A. The energy of a photon is $E = h v$ .

B. The velocity of a photon is c.

C. The momentum of a photon, $p = \frac{h v}{c}$ .

D. In a photon-electron collision, both total energy and total momentum are conserved.

E. Photon possesses positive charge.

Choose the correct answer from the options given below:

0 Follower 6 Views

alok kumar singh

Contributor-Level 10

(A) If $c$ is the velocity of light

so, $E = h ν$ (Energy of photon)

(B) Velocity of photon is equal to velocity of light i.e. c.

$p = \frac{h}{λ}$

$p = \frac{h v}{c}$

(D) In photon-electron collision both total energy and total momentum are conserved.

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

66k Colleges
1.2k Exams
686k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Physics Electrostatic Potential and Capacitance

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience