Physics Electrostatic Potential and Capacitance
Get insights from 132 questions on Physics Electrostatic Potential and Capacitance, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Electrostatic Potential and Capacitance
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
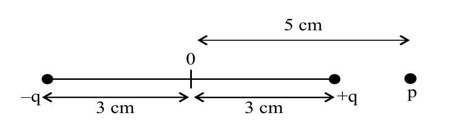
F = (qQ)/ (4πε? r? ²) + (qQ)/ (4πε? r? ²) + (qQ)/ (4πε? r? ²) + (qQ)/ (4πε? r? ²) + .
⇒ F = (qQ)/ (4πε? ) [1/1² + 1/2² + 1/4² + 1/8² + .]
⇒ F = (qQ)/ (4πε? ) [1/ (1 - 1/4)]
⇒ F = (qQ)/ (4πε? ) [4/3] = 10? * 1 * 9 * 10? * (4/3) = 12 * 10³ N
New answer posted
4 months agoContributor-Level 10
The flux φ is calculated as:
φ = (2/5) * 4 * 10³ * 0.4 = 640 Nm²C? ¹
New answer posted
4 months agoContributor-Level 10
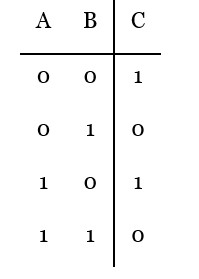
Let the charge on C? be q µC. For the capacitor network:
q/C? = (C? * 10 - q) / C? ⇒ q/8 = (2 * 10 - q) / 2 ⇒ q = 16
New answer posted
4 months agoContributor-Level 10
Initial charge Q = CV = 14 * 10? ¹² * 12 = 168 * 10? ¹² C
Initial energy U_in = ½ CV² = ½ (14 * 10? ¹²) * 12² = 1008 pJ
When the battery is disconnected and a dielectric (k=7) is inserted, the new capacitance is C' = kC.
The charge Q remains constant.
Final energy U_f = Q²/2C' = Q²/ (2kC) = (CV)²/ (2kC) = CV²/ (2k)
U_f = (14 * 10? ¹² * 12²) / (2 * 7) = 144 pJ
Mechanical energy available for oscillation
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers