Physics Oscillations

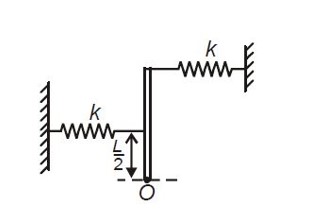
Given mg = kL
∴ Iα = (kLθ.L + k (L/2)²θ - mg (L/2)θ)
(mL²/3)α = kL² (3/4)θ (restoring torque)
α = (9k/4m)θ
∴ ω = (3/2)√ (k/m)

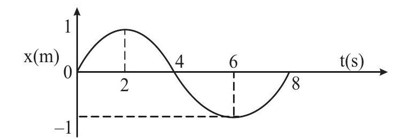
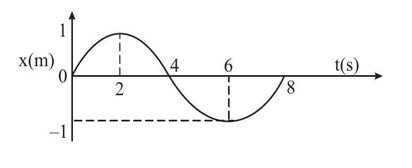
y = A sin (2πt/T)
t? - t? = (T/2π) [sin? ¹ (x? /A) - sin? ¹ (x? /A)]

From x-t graph,

$\begin{array}{rr}& A=1,T=8\\ & \Rightarrow \omega =\frac{2\pi }{T}\\ & \Rightarrow \omega =\frac{\pi }{4}\\ & \text{at}t=2,x=1\\ & a=-{\omega }^{2}x\\ & \Rightarrow \mathrm{a}=\frac{-{\pi }^2}{16}*1\\ & \Rightarrow \mathrm{a}=\frac{-{\pi }^2}{16}\mathrm{m}/{\mathrm{s}}^2\end{array}$

$\omega =100$

$v=\frac{\omega }{2\pi }=\frac{100}{2\pi }=\frac{50}{\pi }\mathrm{H}\mathrm{z}$

Resonance frequency

$v_0=\frac{1}{2\pi \sqrt[]{\mathrm{L}\mathrm{C}}}=\frac{1}{2\pi }\sqrt[]{\frac{1}{10*10*{10}^{-6}}}$

$=\frac{50}{\pi }\mathrm{H}\mathrm{z}$

Displacement equation of SHM of frequency ' $n$  '

$\mathrm{x}=\mathrm{A}\mathrm{s}\mathrm{i}\mathrm{n}?\left(\omega \mathrm{t}\right)=\mathrm{A}\mathrm{s}\mathrm{i}\mathrm{n}?\left(2\pi \mathrm{n}\mathrm{t}\right)$

Now,

Potential energy $U=\frac{1}{2}{\mathrm{k}\mathrm{x}}^2=\frac{1}{2}{\mathrm{K}\mathrm{A}}^2{\mathrm{s}\mathrm{i}\mathrm{n}}^2?2\pi \mathrm{n}\mathrm{t}$

$=\frac{1}{2}{\mathrm{k}\mathrm{A}}^2\left. [\frac{1-\mathrm{c}\mathrm{o}\mathrm{s}?2\pi 2\mathrm{n}\mathrm{t}}{2}\right]$

So frequency of potential energy $=2n$

$\begin{array}{rr}& \mathrm{v}\propto \sqrt[]{\mathrm{T}}\\ & \frac{{\mathrm{v}}_{\mathrm{i}}}{{\mathrm{v}}_{\mathrm{f}}}=\sqrt[]{\frac{1}{2}}=\frac{1}{\sqrt[]{2}}\end{array}$

$\left|\stackrel{?}{\mathrm{F}}\right|=\left|\mathrm{I}\right(\stackrel{?}{\mathrm{L}}*\stackrel{?}{\mathrm{B}}\left)\right|$

$\text{?}\mathrm{}\stackrel{?}{\mathrm{E}}\cdot \mathrm{d}\stackrel{?}{\mathrm{s}}=0\Rightarrow {?}_{\text{net}}={?}_{\text{in}}-{?}_{\text{out}}=0$

$\Rightarrow {?}_{\text{in}}={?}_{\text{out}}$

(A) sin (ωt) + cos (ωt) = √2 sin (ωt + π/4) ⇒ T = 2π/ω
(B) sin² (ωt) = 1/2 - (1/2)cos (2ωt) ⇒ T = 2π/ (2ω) = π/ω
(C) 3cos (π/4 - 2ωt) ⇒ T = 2π/ (2ω) = π/ω
(D) cos (ωt) + cos (2ωt) + cos (3ωt)
Time period of cos (ωt) = 2π/ω
Time period of cos (2ωt) = 2π/ (2ω)
Time period of cos (3ωt) = 2π/ (3ω)
Time period of combined function = 2π/ω

While the particle moves from mean position to displacement, half of its amplitude, its phase changes by π/6 rad. So,
Time taken, t = (π/6)/ω = T/12 = (2/12)s = (1/6)s
a = 6