Quantitative Aptitude Prep Tips for MBA
Get insights from 251 questions on Quantitative Aptitude Prep Tips for MBA, answered by students, alumni, and experts. You may also ask and answer any question you like about Quantitative Aptitude Prep Tips for MBA
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
Average salary of each temporary employee is 600.
1000 temporary employee,
Total salary = 6,00,000
let teaching departement = Rs. x / staff and cleaning department salary = x + 100
Now, 600 (x + 100) + 400 (x) = 6,00,000
x=540
Hence answer, x+100= 540+100=640
New answer posted
3 months agoContributor-Level 10
We have (A – 20) = 0.4 (B + 20), i.e. A – 0.4B = 28
And (B – 40) = 0.4 (A + 40), i.e. B – 0.4A = 56
Solving we get, A = Rs. 60
New answer posted
3 months agoContributor-Level 10
Let speeds of P, Q & R be P, Q & R km/hr respectively.
Thus 4P = 2R
= . (1)
= 5Q = 4R = . (2)
From (1) & (2),
=
=
New answer posted
3 months agoContributor-Level 10
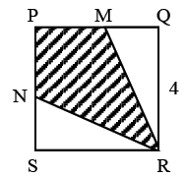
Since M is the midpoint of side PQ, the length of MQ is 2.
Hence, the area of? MQR = * 2 * 4 = 4.
Also area of? NSR = 4. Thus, the unshaded area of the figure = 4 + 4 = 8.
Hence, the area of quadrilateral PMRN
= Area of the square PQRS – The unshaded area of the figure
= 16 – 8 = 8
New answer posted
3 months agoContributor-Level 10
Let n = the number of terms.
Then,
Let d be the common difference.
Then (= the eleventh term) = 17 + 10d
New answer posted
3 months agoContributor-Level 10
Let oil in containers be A & B.
After 1st operation
Container A = 0.4 A
Container B = 0.6 A + B
After 2nd operation
Container A = 0.4 A + 0.3 A + 0.5 B
Container B = 0.3 A + 0.5 B
=
1.6A = 2B
Volume of A : B = 5 : 4.
New answer posted
3 months agoContributor-Level 10
Let the distance be x km and speed be y km/hr and t be the time in hours. Then the equation will be x = yt …. (1),
Therefore,
Also,
On solving the above equations, we get speed is km/hr time is 6 hrs, and distance is 200 km.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers