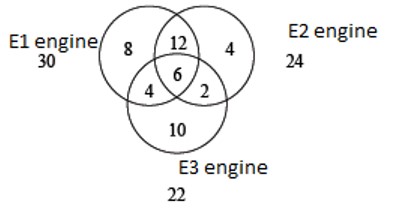
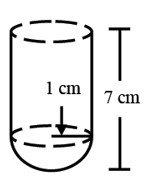
Quantitative Aptitude Prep Tips for MBA
Get insights from 251 questions on Quantitative Aptitude Prep Tips for MBA, answered by students, alumni, and experts. You may also ask and answer any question you like about Quantitative Aptitude Prep Tips for MBA
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
Let f (x) = px2 + qx + k, where p, q and k are integers, and p ≠ 0
f (0) = k = 1
f (x) = px2 + qx + 1
= px2 +qx + k (Differentiate both sides with respect to x)
f' (x) = 2px + q
For maxima or minima f' (x) = 0, x =
f (x) attains maximum at x = 1
q = − 2p
f (1) = p + q + 1 = 3
1 − p = 3
p = − 2
q = 4
f (x) = −2x2 + 4x + 1
f (10) = − 200 + 40 + 1 = −159
New answer posted
3 months agoContributor-Level 10
f (x) = x – x2 + 1
g (x) = x2 + b + 3
f (2) g (1) < 0
(a – 4 + 1) (1 + 6 + 3) < 0
(a – 3) (b + 4) < 0
New answer posted
3 months agoContributor-Level 10
100! has 24 zeroes.
100! + 200! = 100! [1 + 101 * 102 * … * 200]
Which will again give 24 zeroes at the end.
New answer posted
3 months agoContributor-Level 10
Let 2P = 3Q = 4R = 5S = K
Then,
K=1200
Therefore. R = 300, S = 240
Difference=300 - 240 = 60
New answer posted
3 months agoContributor-Level 10
400 students * 80 days = 240 students * d days
d =
The food was to last 80 more days but now it is lasting 53.33 days more.
New answer posted
3 months agoContributor-Level 10
| A | B |
I | 5x | 3x |
II | 4y | 7y |
5x + 4y = 253 …. (1)
3x + 7y = 161 …. (2)
On solving equations (1) & (2), we get
x = 49 and y = 2.
Hence, type I Alloy = 392 kg, and Type II Alloy = 22 kg
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers