Sequences and Series
Get insights from 207 questions on Sequences and Series, answered by students, alumni, and experts. You may also ask and answer any question you like about Sequences and Series
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
104. Given,
Principal amount =? 10000
Amount at end of 1 year =?
=? (10000 + 500)
=? 10500 {Amount paid = principal + S.I. in a year}
Amount at end of 2nd year
=?
=? (10000 + 1000)10500 + 500
=? 11000
Amount at end of 3rd year
=?
=? (1000 + 1500)
=? 11500
So, amount at end of 1st, 2nd, 3rd ………, nth year forms as A.P.
i.e.? 10500? 11000? 115000, ………. with
a = 10500
d = 11000 - 10500 = 500
Now, Amount in 15th year = Amount at end of 14th year
=? 10500 + ( 14 - 1) * 500
=? 10500 + 13 * 500
=? 10500 + 6500
=? 17000
Similarly amount after 20th year, =? 10500+ (20 - 1) * 500
=? 10500 + 19 * 500
=? 10500 + 9500
=
New answer posted
7 months agoContributor-Level 10
103. As the number of letters mailed forms a G.P. i.e., 4, 42, ……., 48
We have,
a = 4
and n = 8
So, Total numbers of letters = 4 + 43 + ……. + 48
= 87380
As amount spent on one postage = 50 paise ?
So, for reqd. postage =?
=? 43690
New answer posted
7 months agoContributor-Level 10
102. Given, cost of scooter = ?22,000
Amount paid =? 4000
Amount unpaid =? 22,000 -? 4000 =? 18,000
Now, Number of installments =Amount unpaid/Amount of each instalment
As he per 10% interest on up unpaid amount and ?1000 each installment
Amount of 1st instalment =? 1000 +? = ?1000 + ?1800 =? 2800
Amount of 2nd installment =? 1000 +? =? 1000 +? 1700 =? 2700
Similarly,
Amount of 3rd installment =? 1000 +? =? 1000 +? 1600 =? 2600
So, Total installment paid =? 2800 +? 1600 =? 2600 + …… upto 18 installment
= 9 [5600 - 1700]
= 9 * 3900
=? 35,000
Total cost of scooter = Amount + Total instal
New answer posted
7 months agoContributor-Level 10
101. Given,
cost of tractor =? 12,000
Amount paid =? 62,000
Amount unpaid =? 12000 -? 6000 =? 6000
So, number of instalments =
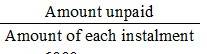
?
= 12 = n
Now, interest on 1st installment = interest on unpaid amount ( i.e.? 6000) for 1 Year.
=? = ?720
Similarly,
Interest on 2nd installment = interest on (? 6000 -? 500) for the next 1 year
=? = ?660
And,
Interest on 2nd installment =?
=? 600
Here, Total (interest per) installment paid =? (720 + 660 + 600 + ……. upto 12 terms)
{ 720 + 660 + 600 …….is an A.P. of a = 720, d = 660 - 720 = - 60}
= 6 [ 1440 -
New answer posted
7 months agoContributor-Level 10
100. Given,
For numerator,
a (nth term) = n (n + 1)2 = n (n + 1)2 = n (n2 + 2n +1) = n3 + 2n2 + n
So,
For denominator,
an (nth term) = n2 (n + 1) = n3 + n2
So,
So,
New answer posted
7 months agoContributor-Level 10
99. The given series is.
+…………. upto nth term,
The nth term is ,
{ A.P. of n terms and a = 1, d = 5-3 = 2}
New answer posted
7 months agoContributor-Level 10
98. Given,
S1 = 1 + 2 + 3 + ………. + n
S2 = 12 + 22 + 32 + ………… + n2
S3 = 13 + 23 + 33 + …………. + n3 =
So, L.H.S.
R.H.S.
L.H.S.
So, 9(S2)2 = S3 ( 1 + 8S1)
New answer posted
7 months agoContributor-Level 10
97. The given series is 3+7+13+21+31+ ……. upto n terms
So, Sum, Sn = 3+7+13+21+31+ ………….+ an-1 + an
Now, taking,
Sn = Sn = [ 3 + 7 + 13 + 21 + 31 + ………. an-1 + an ] [ 3+ 7 + 21 + 31 + … an-1 + an]
0 = [ 3+ (7 - 3) + (13 - 7) + (13 - 7) + (21 - 13) + …….+ (an an-1) - an]
0 = 3 + [ 4 + 6 + 8 +…….+ (n-1) terms] an
{ 4 + 6 + 8 + ……. is sum of A.P. of n 1 terms with a = 4, d = 6- 4 = 2}
an = 3 + n2 + (1 + 2) n + (-1) (2) { (a + b) (a + b) = a2 + (b + c) a + bc }
an = 3 + n2 + n- 2 = n2 + n +1
sum of series,
New answer posted
7 months agoContributor-Level 10
96. Given, series is terms.
So, a20 = ( 20th term of A.P. 2, 4, 6 ….) ( 20th term of A.P. 4,6,8 ………)
i.e. a = 2, d = 4 -2 = 2 i.e. a =4, d = 6- 4 = 2
= [2 + (20- 1)2] [4 + (20-1)2]
= [2+19*2] [4 +19 *2]
= (2+38) (4+38)
= 40*42 = 1680
New answer posted
7 months agoContributor-Level 10
95. (i) Sn = 5+55+555+…………… upto n term
=5(1+11+111+ …………….upto n term )
Multiplying and dividing by 9 we get
(ii)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers
