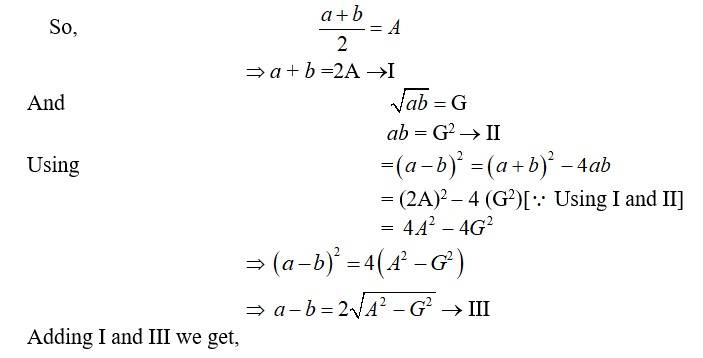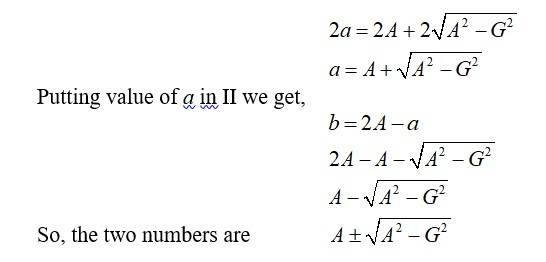Sequences and Series

61. Let a and b be the two number and a> b  so a-b = (+ ve)

60. Let a and b be the two numbers and a>b so a-b = (+ ve)

So, sum of two numbers = 6. G.M of a and b

59. We know that,

G.M between a and b = √ab

Given $\frac{a^{n+1}+b^{n+1}}{a^n+b^n}=\; \surd ab$

$\Rightarrow$ $a^{n+1}+b^{n+1}={\left(ab\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(a^n+b^n\right)$

$\Rightarrow$ $a^{n+1}+b^{n+1}=a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.b^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

$\Rightarrow$ $a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+b^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.b^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

$\Rightarrow$ $a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}.b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{b}^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-b^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$

$\Rightarrow$ $a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left[a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]=b^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left[a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]$

$\Rightarrow$ $\frac{a^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{b^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}=\frac{\left[a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]}{\left[a^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}-b^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right]}$

$\Rightarrow$ ${\left(\frac{a}{b}\right)}^{n+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=1.={\left(\frac{a}{b}\right)}^{?}$

$\Rightarrow$ $n+\frac{1}{2}=0$

$\Rightarrow$ $n=-\frac{1}{2}$

58. Let G₁ and G₂ be the two numbers between 3 and 81 so that 3, G₁, G₂, 81 is in G.P.

So, a = 3

a₄ = ar³ = 81 (when r = common ratio)

$\Rightarrow$ $r^3=\frac{81}{a}=\frac{81}{3}$

$\Rightarrow$ r³ = 27

$\Rightarrow$ r³ = 3³

$\Rightarrow$ r = 3

So, G1 = ar = 33=9 and G₂ = ar² 3´ (3)² =27

57. Let r be the common ratio of the G.P. then,

First term = a₁ = a = a

$a_2=ar=b$

$a_3=a{r}^2=c$

$a_4=a{r}^3=d$

So, L.H.S.= $\left(a^2+b^2+c^2\right)\left(b^2+c^2+d^2\right)$

= $\left[a^2+{\left(ar\right)}^2+{\left(a{r}^2\right)}^2\right]\left[{\left(ar\right)}^2+{\left(a{r}^2\right)}^2+{\left(a{r}^3\right)}^2\right]$

= $\left[a^2+a^2{r}^2+a^2{r}^4\right]\left[a^2{r}^2+a^2{r}^4+a^2{r}^6\right]$

= $a^2\left[1+r^2+r^4\right]a^2{r}^2\left[1+r^2+r^4\right]$

= $a^4{r}^2{\left[1+r^2+r^4\right]}^2$

R.H.S.= ${\left(ab+bc+cd\right)}^2$

= ${\left[a*ar+ar.a{r}^2+a{r}^{2}a{r}^3\right]}^2$

= ${\left[a^{2}r+a^2{r}^3+a^2{r}^5\right]}^2$ $$

= { $a^{2}r{\left[1+r^2+r^4\right]}^2$ }

= $a^4{r}^2{\left[1+r^2+r^4\right]}^2$

L.H.S. = R.H.S.

56. Let a and r be the first term and common difference of the G.P

Thus, Sum of the first on term, $S_n=\frac{a\left(1-r^n\right)}{1-r}$

Let Sn = sum of term from (n+1)^th to (2n)^th  term

= $a{r}^n+a{r}^{n-1}+......+a{r}^{2n-1}$

= $\frac{a{r}^n\left[1-r^n\right]}{1-r}$

[ $?$ the above is a G.P. with first term ar^x and common ratio = $\frac{a{r}^{n+1}}{a{r}^n}=r^{n+1-n}=r$

and number of term from (2n)^th to (n+1)^th = n

So, $\frac{S_n}{S_n}=\frac{\frac{a\left(1-r^n\right)}{1-r}}{\frac{a{r}^n\left(1-r^n\right)}{1-r}}$

= $\frac{a}{a{r}^n}$

= $\frac{1}{r^n}$

55. Given, first term and xth term and a and b

Let r be the common ratio of the G.P.

Then,

Product of x terms, p= $\left(a\right)$ $\left(ar\right)$ $\left(a{r}^2\right)$ …… $\left(a{r}^{n-1}\right)$

p= $\left(a\right)$ $\left(ar\right)\left(a{r}^2\right)$ …. $\left(a{r}^{n-2}\right)\left(a{r}^{n-1}\right)$

= (a *a* ….n term)(r´r²´r³ …. $r^{n-2}*r^{n-1}$ )

= $a^x$ $r^{\left[1+2+3+....\left(n-2\right)+\left(n-1\right)\right]}$

p = $a^n$ $r^{n\left(\frac{n-1}{2}\right)}$

So, $p^2={\left[a^n{r}^n\left(\frac{n-1}{2}\right)\right]}^2$ [We know that,

= $n\frac{\left(n-1\right)}{2}$ [ $1+2+3+...+n=\frac{\left(n-1\right)n}{2}$

= $a^{2n}{r}^{2n}\left(\frac{n-1}{2}\right)$ [So, $1+2+3+....+\left(n-1\right)=\frac{\left(n-1+1\right)\left(n-1\right)}{2}=\frac{n(n-1)}{2}$

= $a^{2n}*r^{n\left(n-1\right)}$

= ${\left(a*a{r}^{n-1}\right)}^n$ $[?$ $a{n}^{n-1}=$ last term = b (given)]

= ${\left(a*b\right)}^n$

54. Let a and r be the first term and common ratio of the G.P.

Then, ap = a

$A{R}^{p-1}=a$ …… I

and aq = b

$A{R}^{q-1}=b$ …….II

Also, ar = c

$A{R}^{r-1}=c$ ….III

Given, L.H.S. = $a^{a-r}$ $b^{r-p}$ $c^{p-q}$

${\left(A{R}^{p-1}\right)}^{q-r}$ ${\left(A{R}^{q-1}\right)}^{r-p}$ $\left(A{R}^{r-1}\right)$ $?$ using I, II and III

$A^{q-r}$ $R^{\left(p-1\right)}$ $A^{r-p}$ $R^{\left(q-1\right)\left(r-p\right)}$ $A^{p-q}$ $R^{\left(r-1\right)\left(p-q\right)}$

$A^{\left[q-r+r-p+p-q\right]}$ $R^{\left[\left(p-1\right)\left(q-r\right)+\left(q-1\right)\left(n-p\right)+\left(x-1\right)\left(p-q\right)\right]}$

A0 R[pqprq+r+qrpqr+p+prqrp+q] $$

$1*$ $R^{\left[pq-pq+pr-pr+q-q+r-r+qr-qr+p-p\right]}$

= R

= 1

= R.H.S

53. Let the four numbers is G.P. be a, ar, ar², ar³

Given, $a{r}^2-a=9$

$\Rightarrow$ $a\left(r^2-1\right)=9$ I

And $\Rightarrow$ $ar-a{r}^3=18$

$\Rightarrow$ $ar\left(1-r^2\right)=18$

$\Rightarrow$ $\left(-1\right)ar\left(x^2-1\right)=18$

$\Rightarrow$ $ar\left(x^2-1\right)=-18$ II

Dividing II by I we get,

$\frac{ar\left(r^2-1\right)}{a\left(r^2-1\right)}=\frac{-18}{9}$

r = 2

So, putting r = 2 in I we get ,

$\Rightarrow$ $a\left[{\left(-2\right)}^2-1\right]=9$

$\Rightarrow$ $a\left[4-1\right]=9$

$\Rightarrow$ $a*3=9$

$\Rightarrow$ $a\frac{9}{3}$

$\Rightarrow$ a = 3

$\therefore$ The four numbers are 3, 3´(-2), 3´(-2)², 3´(-2)³

$\Rightarrow$ 3, 6, 12, 24

The product of corresponding terms of the given sequence are

= $a*A+\left(ar\right)*AR+\left(a{r}^2\right)*A{R}^2+......\left(a{r}^{x?1}\right)\left(A{R}^{x?1}\right)$

= $aA+\left(aA\right)+\left(rR\right)+\left(aA\right)$ $......+\left(aA\right){\left(rR\right)}^{x?1}$

So, looking at the sequence forms a G.P.

(above the)

With common ratio = $\frac{\left(aA\right)\left(rR\right)}{\left(aA\right)}=rR$