Sequences and Series

72. Given that,

a_n = n(n + 1)(n + 4)

= n(n² + 4n + n + 4)

=n(n² + 5n + 4)

= x³ + 5x² + 4x

So, sum of terms, S_n = $\sum n^3+5\sum n^2+4{\displaystyle \sum _{}^{}n}$

$={\left[\frac{n(n+1)}{2}\right]}^2+5*\frac{n(n+1)(2n+1)}{6}+\frac{4\stackrel{?}{n}(n+1)}{2}$

$=\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2}+\frac{5(2n+1)}{3}+4\right]$

$=\frac{n(n+1)}{2}\left[\frac{3n(n+1)+2*5(2n+1)+6*4}{6}\right].$

$=\frac{n(n+1)}{2}\left[\frac{3n^2+3n+20n+10+24}{6}\right]$

$=\frac{n(n+1)}{2}\left[\frac{3n^2+23n+34}{6}\right]$

$=\frac{n(n+1)\left(3n^2+23n+34\right)}{12}$

$=\frac{n(n+1)}{12}$ $\left(3n^2+6n+17n+34\right)$

$=\frac{n(n+1)}{12}[3n^2+23n+34]$

71. The given series is 1² + (1² + 2²) + (1² + 2² + 3²) + …

So, nth term well be

a_n =1² + 2² + 3² + … + n².

$=\frac{n(x+1)(2n+1)}{6}$

$=\frac{n\left(2x^2+n+2n+1\right)}{6}$

$=\frac{n\left(2n^2+3n+1\right)}{6}$

$=\frac{2n^3+3n^2+n}{6}$

$=\frac{x^3}{3}+\frac{x^2}{2}+\frac{x}{6}$

So, S_n = $\frac{1}{3}\sum n^3+\frac{1}{2}\sum n^2+\frac{1}{6}{\displaystyle \sum _{i=1}^{n}n}$

$=\frac{1}{3}{n}^2\frac{{(n+1)}^2}{4}+\frac{1}{2}\frac{n(n+1)(2n+1)}{6}+\frac{1}{6}·\frac{n(n+1)}{2}$

$=\frac{n(x+1)}{6}\left[\frac{n(x+1)}{2}+\frac{(2n+1)}{2}+\frac{1}{2}\right]$

$=\frac{n(n+1)}{6}\left[\frac{n^2+n+2n+1+1}{2}\right]$

$=\frac{n(n+1)}{12}\left[n^2+5n+2n+2\right]$

$=\frac{n(n+1)(n+1)(n+2)}{12}$

$=\frac{n{(n+1)}^2(n+2)}{12}$

70. The given series is 3 8 + 11 + 9 14 + …

So, a_n= (nth term of 3, 6, 9, …) (nth term of 8, 11, 14, …)

i e, a = 3, d = 6- 3 = 3i e, a= 8, d = 11- 8 = 3

= [3 + (n- 1) 3] [8 + (n -1) 3]

= [3 + 3n- 3] [8 + 3n -3]

= 3n (3n + 5)

= 9n² + 15n.

So, S_n = 9∑n² + 15∑ n.

$=9*\frac{n(n+1)(2n+1)}{6}+15*\frac{n(n+1)}{2}$

$=\frac{3}{2}n(n+1)(2n+1)+\frac{15}{2}n(n+1)$

$=\frac{3n}{2}(n+1)[2n+1+5]$

$=\frac{2n(n+1)}{2}[2n+6]$

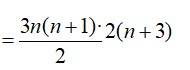
= 3n (n + 1) (n + 3)

69. The given series is 5² + 6² + 7² + … + 20²

This can be rewritten as (1² +2² + 3² + 4² + 5² + 6² + 7² + … + 20²) - (1² + 2² + 3² + 4²)

So, sum = (1² + 2² + 3² + 4² … + 20²) - (1² + 2²+ 3² + 4²)

$=$${\displaystyle \underset{}{\overset{}{}}}$${\displaystyle \sum _{i=1}^{20}{n}^2}-{\displaystyle \sum _{i=1}^4{n}^2}$

$=\frac{20(20+1)(2*20+1)}{6}-\frac{4(4+1)(4*2+1)}{6}$

$=\frac{20*21*41}{6}-\frac{4*5*9}{6}$

= 2870 30

= 2840.

68. The given series is $\frac{1}{1*2}+\frac{1}{2*3}+\frac{1}{3*4}+?$

So, an = $\frac{1}{\left(n^{}1,2,3\dots \right)}*\frac{1}{\left(n^{ }ten 2,3,4\dots \right)}$

$=\frac{1}{[1+(n-1)1]}*\frac{1}{[2+(n-1)1]}$

$=\frac{1}{(1+x-1)}*\frac{1}{(2+n-1)}$

$=\frac{1}{n(n+1)}$

$=\frac{(n+1)-n}{n(n+1)}$

$=\frac{(n+1)}{n(n+1)}-\frac{n}{n(n+1)}$

$a_n=\frac{1}{n}-\frac{1}{n+1}$

So. Putting n = 1, 2, 3….n.

a₁ = $\frac{1}{1}-\frac{1}{2}$

a₂ = $\frac{1}{2}-\frac{1}{3}$

a₃ = $\frac{1}{3}-\frac{1}{4}\dots .$

So, adding. L.H.S and R.H.S. up ton terms

a₁ + a² + a₃ + … + a_n = $\left[\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+?\frac{1}{n}\right]-[\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+?·\frac{1}{n}+\frac{1}{n+1}]$

 S_n = 1 $\frac{1}{n+1}$ { equal terns cancelled out}

 S_n = $\frac{n+1-1}{.n-1}$

 S_n = $\frac{n}{n+1}$

67. The given series is 3 * 1² + 5 * 2² + 7 * 3² + ….

So,a_n = (n^th term of A P 3, 5, 7, .) (n^th term of A P 1, 2, 3, ….)²

a = 3, d = 5 -3 = 2a = 1, d = 2 -1 = 1.

= [3 + (n- 1) 2] [1 + (n- 1) 1]²

=[3 + 2n- 2] [1 + n- 1]²

(2n + 1)(n)²

= 2n³ + n²

So, = 5n2∑n³ + ∑n²

$=2·{\left[\frac{n^{}(n+1)}{2}\right]}^2+\left[\frac{n(n+1)(2n+1)}{6}\right]$

$=\frac{n(n+1)}{2}\left[2·\frac{n(n+1)}{2}+\frac{(2n+1)}{3}\right]$

$=\frac{n(n+1)}{2}\left[\frac{3n(n+1)+(2n+1)}{3}\right]$

$=\frac{n(n+1)}{2}\left[\frac{3n^2+3n+2n+1}{3}\right]$

$=\frac{n}{2}(n+1)·\left[\frac{3n^2+5n+1}{3}\right]$

$\frac{n(n+1)\left(3n^2+5n+1\right)}{6}$

65. Given series is 1*2+2 *3+3* 4+4* 5+…

So, an (nth term of A.P 1, 2, 3…) (nth term of A.P. 2, 3, 4, 5…)

i e, a = 2, d = 2 -1 = 1i e, a = 2, d = 3 - 2 = 1

= [1 + (n- 1) 1] [2 + (n -1) 1]

= [1 + n- 1] [2 + n -1]

= n (n -1)

= n²-n.

S_n (sum of n terms of the series) = ∑n² + ∑n.

S_n = $\frac{n(n+1)(2n+1)}{6}$ + $\frac{n(x+1)}{2}$

= $\frac{n(n+1)}{2}\left[\frac{2n+1}{3}+1\right]$

= $\frac{n(n+1)}{2}\left[\frac{2n+1+3}{3}\right]$

$=\frac{n(n+1)}{2}*\frac{(2n+4)}{3}$

$=\frac{n(n+1)*2(n+2)}{2*3}$

$=\frac{n(n+1)(n+2)}{3}$

64. Let a and b be the roots of quadratic equation

So, A.M = 8

$\Rightarrow$ $\frac{a+b}{2}=8$ a + b =16 ….I

G.M. = 

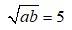
$\Rightarrow$ ab = 25…. II

We know that is a quadratic equation

$x^2-x$  (sum of roots) + product of roots = 0

$x^2-x\left(a+b\right)+ab=0$

$x^2-16x+25=0$ using I and II

Which is the reqd. quadratic equation 

63. Given,

Principal value, amount deposited, P= ?500

Interest Rate, R= 10

Using compound interest = simple interest + $\frac{P*R*time}{100}$

Amount at the end of 1st year

= $500+\frac{500*10+1}{100}=500\left(1+0.1\right)=500*1.1$

= ?500* (1.1)

Amount at the end of 2nd year

= $500\left(1.1\right)+\frac{500*1.1*10*1}{100}$

= $500\left(1.1\right)\left(1+0.1\right)$

= ?500 (1.1)²

Similarly,

Amount at the end of 3rd year = ?500 (1.1)³

So, the amount will form a G.P.

? 500 (1.1)? 500 (1.1)²?500 (1.1)³, ……….

$\therefore$ After 10 years = ?500 (1.1)¹⁰

62. Since the numbers of bacteria doubles every hour. The number after every hour will be a G.P

So, a=30

r=2

$\therefore$ At end of 2^nd hour, a₃ (or 3^rd term) = $a{r}^2=30*2^2$

= 30*2⁴

= 120

At end of 4^th hour, a₅ (r 4^th  term) = $a{r}^4$

= 30*2⁴

= 30*16

= 480

Following the trend,

And at the end of nth hour, an+1= $a{r}^{n+1-1}=a{r}^n$

= 30 *2ⁿ