Solid State

1.34 (i) The efficiency of packing in case of simple cubic unit cell is given below: 
A simple cubic unit cell contains one atom per unit cell.
Also, a=2r, where a is the edge length and r is the radius of atom. Total volume of unit cell = a³
Packing efficiency = Volume of one sphere / Total volume of unit cell * 100

Packing Effieciency = 4/3πr³ / 8r³ X 100 = 52.4%

(ii) The efficiency of packing in case of body-centred cubic unit cell is given below:
A body-centred cubic unit cell containstwo atoms per unit cell.
Also, √3a = 4r,where a isthe edge length and r isthe radius of atom.
Total volume of unit cell = a³
Packing efficiency = Volume of one sphere / Total volume of unit cell * 100

Packing efficiency = 16/3πr³ / 16√2r³ x 100 = 74%

(i) Both metallic and ionic crystals have strong forces of attraction between their atoms or ions. In metallic crystals there is a strong metallic bond present between electrons and positively charged ions. In ionic crystals there are strong ionic bonds between anions and cations. Both of them conduct electricity,  
but metallic crystals conduct electricity in all three states of matter while ionic crystals conduct electricity only in molten state.
(ii) The ionic solids are hard and brittle because they have strong electrostatic forces of attraction between the anions and cations .As a result the anions and cations are tightly held by these forces and due to which they are unable to move and they are fixed at one position. So when force is applied to break them, they appear to be hard

1.31 (i) In hexagonal close packing (hcp), the spheres of the third layer are vertically above the spheres of the first layer. It means tetrahedral voids of the second layer are covered by the spheres of the third layer. The AB. type.In cubic close packing (ccp), the spheres of third layer cover the octahedral voids of second layer. But the spheres of the fourth layers are aligned with those of the first layer. The pattern is ABC. type.

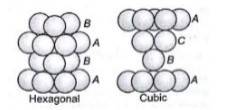
(ii) Crystal lattice is the three dimensional arrangement of identical point in the space which represent how the constituent particles (atoms, ions, molecules) are arranged in a crystal.Unit cell is the smallest portion of a crystal lattice which, when repeated in different directions, generates the entire lattice

(iii) Tetrahedral voids are surrounded by four spheres which lie at the vertices of a regular tetrahedron. There are 2 tetrahedral voids per atom in a crystal.
Octahedral voids are surrounded by six spheres and formed by a combination of two triangular voids of the first and second layer. There is one octahedral void per atom in a crystal.

1.30 Stability of a crystal is directly proportional to the magnitude of its melting points. Higher is the magnitude of forces holding the constituent particles together, higher will be the melting point and higher will be the stability. Thus ionic crystals (NaCl, KNO3 etc.) have very high melting points and stable crystal lattices. On other hand, molecular solids (naphthalene, iodine etc.) have low melting points and low stability.

The melting points of solid water, ethyl alcohol, diethyl ether and methane are 273 K, 155.8 K, 156.8 K and 90.5 K respectively.Solid water and ethyl alcohol have higher melting points due to presence of inter-molecular hydrogen bonds. Since the extent of hydrogen bonding in solid water is greater than the extent of hydrogen bonding in ethyl alcohol, the melting point of solid water is higher than the melting point of ethyl alcohol. 
Polar diethyl ether involves dipole-dipole interactions. Non polar methane involves weak van there Waals forces (London dispersion forces) which are weaker than dipole-dipole interactions. Hence, the melting point of methane is much lower than the melting point of diethyl ether.