Tags Work, Energy and Power

Work, Energy and Power

Get insights from 177 questions on Work, Energy and Power, answered by students, alumni, and experts. You may also ask and answer any question you like about Work, Energy and Power

Follow Ask Question

177

Questions

Discussions

Active Users

Followers

New answer posted

2 months ago

Work, Energy and Power Class 11th

A particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration (a) is varying with time t as a = k² rt², where k is a constant. The power delivered to the particle by the force acting on it is given as

0 Follower 2 Views

Raj Pandey

Contributor-Level 9

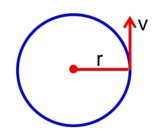
a = k2rt2

$\Rightarrow \frac{v^{2}}{r} = k^{2} r t^{2}$

$\Rightarrow v = k r t$

$a_{t} = \frac{d v}{d t} = k r$

? tangential force, F_t = ma_t = mkr

$∴ P o w e r d e l i v e r e d, P = F_{t} v = (m k r) (k r t) = m k^{2} r^{2} t$

Note ® Power delivered by centripetal force will be zero.

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

In the given figure, the block of mass m is dropped from the point 'A'. The expression for kinetic energy of block when it reaches point 'B' is

0 Follower 3 Views

alok kumar singh

Contributor-Level 10

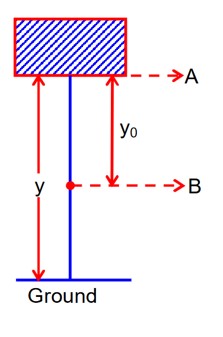
According to conservation of energy, we can write

Gain in kinetic energy = Loss in potential energy

$\Rightarrow$ K_f – K_in = U_in - U_f

$\Rightarrow$ K - = mgy – mg (y – y₀) = mgy₀

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

A 1kg particle is moving unidirectionally on a horizontal plane under the action of power $P = - 2 v^{3}$ , of power supplying energy source. The velocity (v) - time (t) graph that describes the motion of the particle is shown in figure. (Graphs are drawn schematically and are not to scale) The value of $t_{0}$ in graph is sec. Find 8x

0 Follower 2 Views

Raj Pandey

Contributor-Level 9

Kindly consider the following Image

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

A particle of mass 2 kg is moving in the direction of positive x-axis. Initial velocity of the particle is 1 m/s. The instantaneous power vs time graph of the particle is shown in the figure. Find the velocity of the particle at 7 seconds.

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

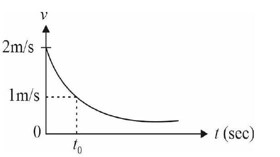
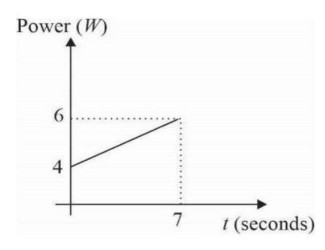
ΔW = area under P — t graph
= (1/2) (4 + 6) * 7 = 35 J
Work done = change in KE ⇒ 35 = (1/2) * 2 * v² - (1/2) * 2 * (1)² ⇒ v = 6 m/s

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

In an imaginary electric field, the electric potential energy of an electron at a distance r from the centre of force field is given by U = kr², where k is a positive constant of appropriate dimensions. If the electron is moving in a circular orbit of radius r about the centre, then the orbital time period of the electron is proportional to:

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

U = kr² ⇒ F = -dU/dr = -2kr ; 2kr = mv²/r ⇒ v = √ (2k/m) or T = 2πr/v = 2π√ (m/2k)

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

A smooth spherical ball strikes a smooth horizontal floor at an angle $θ = 45^{?}$ . The coefficient of restitution between the ball and the floor is $e = \frac{1}{2}$ . The fraction of its kinetic energy lost in collision is: (there is no rotational kinetic energy before or after collision)

0 Follower 1 View

Raj Pandey

Contributor-Level 9

Vertical component of velocity just after collision $= \frac{u}{2 \sqrt[]{2}}$

$k_{i} = \frac{m u^{2}}{2} k_{f} = \frac{1}{2} m \frac{u^{2}}{2} + \frac{1}{2} m \frac{u^{2}}{8} = \frac{5 m u^{2}}{16}$ $\frac{}{}$

Fraction $= \frac{k_{i} - k_{f}}{k_{i}} = 1 - \frac{\frac{5 m u^{2}}{16}}{\frac{m u^{2}}{2}} = 1 - \frac{5}{8} = \frac{3}{8}$

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

What minimum speed does a 100g particle need At point B to reach point A? The graph shows potential energy versus position.

0 Follower 6 Views

alok kumar singh

Contributor-Level 10

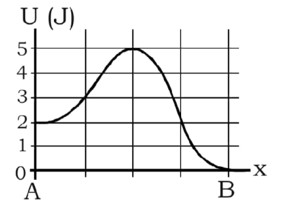
To reach at point A particle must cross the peak point.

Loss in KE = gain in PE

$\frac{1}{2} * \frac{100}{1000} * v^{2} = (5 - 0)$

v² = 100

v = 10 m/s

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

Figure shown two blocks A and B having mass 2kg and 4kg moving with a speed 4 m/sec and 2 m/sec respectively. The maximum compression in the spring and final velocity of 2kg block and respectively.

0 Follower 4 Views

alok kumar singh

Contributor-Level 10

$\frac{1}{2} μ v_{r}^{2} = \frac{1}{2} k x^{2}$

$x = {V_{r e r}}^{2} \sqrt[]{\frac{μ}{k}}$

$= 2 * \sqrt[]{\frac{8 / 6}{10}} = \sqrt[]{\frac{8}{15}}$

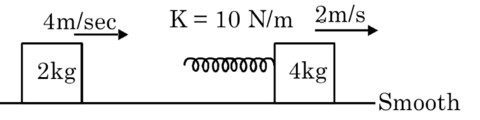
From conservation of momentum

2 * 4 + 4 * 2 = 2v₁ + 4v₂

8 = v₁ + 2v₂ ….(1)

From conservation of energy

$\frac{1}{2} * 2 * 4^{2} + \frac{1}{2} * 4 * 2^{2} = \frac{1}{2} * 2 * v_{1}^{2} + \frac{1}{2} * 4 * v_{2}^{2}$ ….(ii)

On solving $v_{1} = \frac{4}{3} m / s, v_{2} = \frac{10}{3} m / s$

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

A plank of mass 5 kg in kept on a smooth surface. A block of 1 kg is kept on it and is given a velcoity of 12 m/s. There is friction between the block and the plank. Assuming the plank to be very long, find the magnitude of work done (in Joules) by friction on block till the relative sliding between them stops.

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

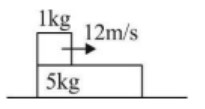
When relative sliding stops, both move with same velocity.
Only friction acts in horizontal direction.
∴ for system no external force, we can apply conservation of momentum.
1 * 12 + 5 * 0 = 6 * v
v = 2 m/s
Now work done by friction on block = change in kinetic energy of block
w = (1/2)m (2² - 12²) = (1/2) (1) (4 - 144) = (1/2) (-140) = -70 J

0 0

New answer posted

2 months ago

Work, Energy and Power Class 11th

An inclined plane in bent in such a way that the vertical cross-section is given by y $= \frac{x^{2}}{4}$ where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction $μ$ = 0.5, the maximum height in cm at with a stationary block with not skip downward is ____________cm.

0 Follower 2 Views

alok kumar singh

Contributor-Level 10

If the block does not slide,

mg sin $θ \leq μ m g c o s θ$

$\Rightarrow t a n θ \leq μ \Rightarrow \frac{d y}{d x} \leq μ \Rightarrow \frac{x}{2} \leq 0.5 \Rightarrow x \leq 1 m .$

Thus, $y \leq \frac{1^{2}}{4} = 0.25 m = 25 c m .$

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
679k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Work, Energy and Power

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience