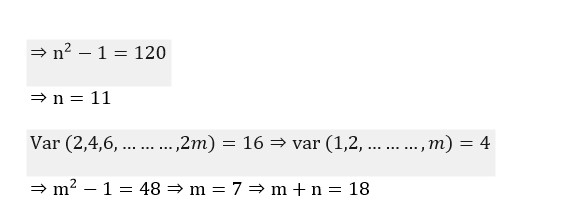Class 11th

$m=\rho \pi r^{2}1$

$\begin{array}{rr}& \rho =\frac{\mathrm{m}}{\pi {\mathrm{r}}^{2}1}\\ & \frac{\mathrm{\Delta }\rho }{\rho }=\frac{\mathrm{\Delta }\mathrm{m}}{\mathrm{m}}+\frac{2\mathrm{\Delta }\mathrm{r}}{\mathrm{r}}+\frac{\mathrm{\Delta }\mathrm{l}}{1}\\ & \frac{\mathrm{\Delta }\rho }{\rho }*100=\frac{0.002}{0.4}*100+\frac{2*0.001}{0.3}*100+\frac{0.02}{5}*100\\ & =\frac{0.2}{0.4}+\frac{0.2}{0.3}+\frac{2}{5}\\ & =0.5+0.67+0.4\\ & =1.57\\ & =1.6\mathrm{\%}\end{array}$

As the factors controlling temperature and voltage supply are beyond prediction and control so the error occurred due to unpredictable fluctuations of temperature and voltage would be random errors.

Kindly consider the following Image 

lim (x→0) [a e? - b cos (x) + c e? ] / (x sin (x) = 2
Using Taylor expansions around x=0:
lim (x→0) [a (1+x+x²/2!+.) - b (1-x²/2!+.) + c (1-x+x²/2!+.)] / (x * x) = 2
lim (x→0) [ (a-b+c) + x (a-c) + x² (a/2+b/2+c/2) + O (x³)] / x² = 2
For the limit to exist, the coefficients of lower powers of x in the numerator must be zero.
a - b + c = 0
a - c = 0 ⇒ a = c
Substituting a=c into the first equation: 2a - b = 0 ⇒ b = 2a.
The limit becomes: lim (x→0) [x² (a/2 + b/2 + c/2)] / x² = (a+b+c)/2
(a + b + c) / 2 = 2 ⇒ a + b + c = 4.

|z+i|/|z-3i| = 1 ⇒ |z+i| = |z-3i|. This means z is on the perpendicular bisector of the segment from -i to 3i. The midpoint is i, so z = x+i.
w = z? - 2z + 2. Let z = x + iy.
w = (x² + y²) - 2 (x + iy) + 2 = (x² - 2x + 2 + y²) - 2iy.
Re (w) = x² - 2x + 2 + y² = (x - 1)² + 1 + y².
From the first condition, y=1. Re (w) = (x - 1)² + 1 + 1 = (x - 1)² + 2.
Re (w) is minimum for x = 1.
The common z is z = 1 + i.
w = (1+i) (1-i) - 2 (1+i) + 2 = 2 - 2 - 2i + 2 = 2 - 2i.
w² = (2 - 2i)² = 4 (1 - 2i - 1) = -8i.
w? = (-8i)² = -64 ∈ R.
∴ least n ∈ N for which w? ∈ R is n=4.

Var (1, 2, ., n) = (Σn²/n) - (Σn/n)² = 10.
(n (n+1) (2n+1)/6n) - (n (n+1)/2n)² = 10.
(n+1) (2n+1)/6 - (n+1)/2)² = 10.
(n+1)/12 * [2 (2n+1) - 3 (n+1)] = 10.
(n+1)/12 * (4n+2 - 3n-3) = 10.
(n+1) (n-1)/12 = 10.
n² - 1 = 120 ⇒ n² = 121 ⇒ n = 11.

Var (2, 4, ., 2m) = Var (2* (1, 2, ., m) = 2² * Var (1, 2, ., m) = 16.
4 * Var (1, 2, ., m) = 16.
Var (1, 2, ., m) = 4.
Using the formula from above: (m²-1)/12 = 4.
m² - 1 = 48 ⇒ m² = 49 ⇒ m = 7.
m + n = 7 + 11 = 18.

Digits are 1, 3, 5, 7, 9. We need to form a 6-digit number where exactly one digit is repeated.

Choose the digit to be repeated:? C? ways.

Choose the positions for these two repeated digits:? C? ways.

Arrange the remaining 4 distinct digits in the remaining 4 places:? P? = 4! ways.
Total numbers =? C? *? C? * 4! = 5 * 15 * 24 = 1800.
The solution in the image 5/2 (6!) seems to follow a different logic which is unclear. 5 * (6!/2) = 5 * 360 = 1800. This logic is: choose one of 5 digits to repeat. Arrange the 6 digits, and since two are identical, divide by 2!