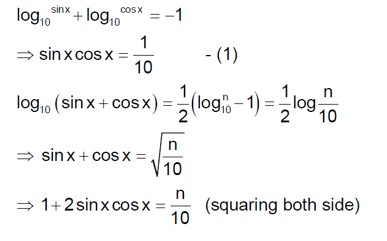Class 11th

Let n be a positive integer. Let A = ∑_{k=0 to n} (-1)ᵏ ⁿCₖ [ (1/2)ᵏ + (3/4)ᵏ + (7/8)ᵏ + (15/16)ᵏ + (31/32)ᵏ ]. If 63A = 1 - 1/2³⁰, then n is equal to.

0 Follower 10 Views

Contributor-Level 10

0 0

New answer posted

3 months ago

Let Sₙ(x) = logₐ^(1/2) x + logₐ^(1/3) x + . up to n-terms. Where a > 1. If S₂₄(x) = 1093 and S₁₂(2x) = 265, then the value of a is equal to.

0 Follower 7 Views

Contributor-Level 10

S? (x) = log? ¹? ²x + log? ¹? ³x + .
This is incorrect; the bases are numbers, not powers of 'a'. Let's assume the bases are 1/2, 1/3, 1/6, 1/11, .
The series is S' = 2, 3, 6, 11, 18, .
The differences are 1, 3, 5, 7, . which is an AP.
The n-th term t? is a quadratic in n.
t? = An² + Bn + C.
t? =A+B+C=2
t? =4A+2B+C=3
t? =9A+3B+C=6
Solving these, we get 3A+B=1 and 5A+B=3, which gives 2A=2, A=1. Then B=-2, C=3.
t? = n² - 2n + 3 = (n-1)² + 2.
The solution confirms this finding t? = 2 + (n-1)².

0 0

New answer posted

3 months ago

If the points of intersections of the ellipse x²/16 + y²/b² = 1 and the circle x² + y² = 4b, b > 4 lie on the curve y² = 3x², then b is equal to :

0 Follower 2 Views

Contributor-Level 10

The point of intersection of the ellipse x²/16 + y²/b² = 1 and the curve y² = 3x² lies on both.
Substitute y² = 3x² into the ellipse equation:
x²/16 + 3x²/b² = 1
x² (1/16 + 3/b²) = 1
x² (b² + 48) / 16b² = 1
x² = 16b² / (b² + 48).
For a solution to exist, we need x² > 0, which is true if b≠0.
The problem seems to have a condition missing or misinterpreted in the OCR. The provided solution also shows x² + y² = 4b, which might be another curve involved. Assuming the point lies on x²+y²=4b.

x² + 3x² = 4b => 4x² = 4b => x² = b.
Substitute x²=b into the ellipse equation: b/16 + 3b/b² = 1 (assuming y²=3b).
b/16 + 3/b = 1

...more

0 0

New answer posted

3 months ago

Let A(-1,1), B(3, 4) and C(2,0) be given three points. A line y = mx, m > 0, intersects lines AC and BC at point P and Q respectively. Let A? and A? be the area of ?ABC and ?PQC respectively, such that A? = 3A?, then the value of m is equal to:

0 Follower 10 Views

Class 11th Ncert Solutions Maths class 11th

Contributor-Level 10

0 0

New answer posted

3 months ago

If for x ∈ (0, π/2), log?sinx + log?cosx = -1 and log?(sinx + cosx) = ½(log?n - 1), n > 0, then the value of n is equal to :

0 Follower 1 View

Contributor-Level 9

Kindly consider the following Image

0 0

New answer posted

3 months ago

The number of elements in the set {x ∈ R : (|x| - 3)|x + 4| = 6} is equal to :

0 Follower 9 Views

Contributor-Level 9

(|x| - 3)|x + 4| = 6

Case (i) x < -4
(-x - 3) (- (x + 4) = 6
(x + 3) (x + 4) = 6 ⇒ x² + 7x + 12 = 6 ⇒ x² + 7x + 6 = 0
(x + 1) (x + 6) = 0 ⇒ x = -6 (since x < -4)

Case (ii) -4 ≤ x < 0
(-x - 3) (x + 4) = 6
⇒ -x² - 7x - 12 = 6
⇒ x² + 7x + 18 = 0
The discriminant is D = 7² - 4 (1) (18) = 49 - 72 < 0, so no real solution.

Case (iii) x ≥ 0
(x - 3) (x + 4) = 6
⇒ x² + x - 12 = 6
⇒ x² + x - 18 = 0
x = [-1 ± √ (1² - 4 (1) (-18)] / 2 = [-1 ± √73] / 2
Since x ≥ 0 ⇒ x = (√73 - 1) / 2
Only two solutions.

0 0

New answer posted

3 months ago

Consider three observations a, b and c such that b = a + c. If the standard deviation of a + 2, b + 2, c + 2 is d, then which of the following is true?

0 Follower 3 Views

Contributor-Level 9

Variance of a, b, c & a+2, b+2, c+2, are same.
Given: b = a + c (i)
d² = (1/3) (a² + b² + c²) - [ (a+b+c)/3]²
as a + c = b
d² = (1/3) (a² + b² + c²) - (2b/3)²
9d² = 3 (a² + b² + c²) - 4b²
⇒ b² = 3 (a² + c²) - 9d²

0 0

New answer posted

3 months ago

Let a complex number z, |z| ≥ 1, satisfy log?/√² (|z|+11)/(|z|-1)² ≤ 2. Then, the largest value of |z| is equal to…

0 Follower 2 Views

Contributor-Level 9

log? /? [ (|z|+11)/ (|z|-1)²] < 2
(|z|+11)/ (|z|-1)² > (1/2)²
(|z|+11)/ (|z|-1)² > 1/4
⇒ 4|z| + 44 > |z|² - 2|z| + 1
⇒ |z|² - 6|z| - 43 < 0

⇒ |z| - 7 ≤ 0
∴ |z|max = 7

0 0

New answer posted

3 months ago

The least value of |z| where z is complex number which satisfies the inequality exp( ((|z|+3)(|z|-1))/(|z|+1) logₑ2 ) ≥ log_√2 |5√7 + 9i|, i = √-1, is equal to :

0 Follower 6 Views

Contributor-Level 10

The inequality is experience ( (|z|+3) (|z|-1) / (|z|+1) * log?2 ) ≥ log√? 16.
The right side is log? (1/2) 16 = log? (2? ¹) 2? = (4/-1)log?2 = -4. This seems incorrect.
Let's assume the base of the log on the right is √2. log√? 16 = log? (1/2) 2? = 2 * log?2? = 8.
The inequality becomes: 2^ (|z|+3) (|z|-1) / (|z|+1) ≥ 8 = 2³.
So, (|z|+3) (|z|-1) / (|z|+1) ≥ 3.
Let |z| = t. (t+3) (t-1) / (t+1) ≥ 3
t² + 2t - 3 ≥ 3t + 3
t² - t - 6 ≥ 0
(t-3) (t+2) ≥ 0
Since t = |z| ≥ 0, we must have t-3 ≥ 0.
So, t ≥ 3, which means |z| ≥ 3.
The minimum value of |z| is 3.

0 0

New answer posted

3 months ago

Let C be the locus of the mirror image of a point on the parabola y² = 4x with respect to the line y = x. Then the equation of tangent to C at P(2, 1) is :

0 Follower 4 Views