Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 9
(3¹/? + 5¹/? )?
General term =? C? (3¹/? )? (5¹/? )? =? C? 3^ (60-r)/4) 5^ (r/8)
Terms are rational for r being a multiple of 8 and (60-r) being a multiple of 4.
If r is a multiple of 8, then 60-r is 60 - 8k. Since 60 is a multiple of 4, 60-8k is also a multiple of 4.
So, we just need r to be a multiple of 8.
r = 0, 8, 16, 24, 32, 40, 48, 56. (Total 8 rational terms)
Total terms are 61.
Number of irrational terms = 61 - 8 = 53 = n.
∴ n - 1 = 52.
New answer posted
3 months agoContributor-Level 10
g (f (x) = f² (x) + f (x) - 1.
g (f (5/4) = f² (5/4) + f (5/4) - 1.
Given g (f (5/4) = 5/4, let f (5/4) = y.
-5/4 = y² + y - 1 (There appears to be a typo in the image's solution)
y² + y - 1 + 5/4 = 0
y² + y + 1/4 = 0
(y + 1/2)² = 0
y = -1/2.
So, f (5/4) = -1/2.
New answer posted
3 months agoContributor-Level 9
Let z = αi + βj be a complex number & √3i + j = (√3 + i) where I = √-1.
|z| = |z - (√3 + i)| and |z| = |√3 + i| = 2.
This implies z lies on the perpendicular bisector of the segment from 0 to √3+i and on a circle of radius 2 centered at the origin.
z = (√3 + i) ( (1+i)/√2 )
z = (1/√2) [ (√3 - 1) + I (√3 + 1)]
∴ α = (√3 - 1)/√2, β = (√3 + 1)/√2
Area of required triangle = (1/2) * base * height = (1/2) * |α| * |β| * 2 (This seems to be area of triangle with vertices 0, z, and another point)
The provided calculation: Area = (1/2) * | (√3-1)/√2| * | (√3+1)/√2| = (1/2) * (3-1)/2 = 1/2.
New answer posted
3 months agoContributor-Level 10
y = √ (2cos²α / (sinα cosα) + 1/sin²α)
y = √ (2cotα + cosec²α)
y = √ (2cotα + 1 + cot²α) = √ (1 + cotα)²) = |1 + cotα|.
Given α is in a range where 1+cotα is negative, y = -1 - cotα.
dy/dα = - (-cosec²α) = cosec²α.
At α = 5π/6, dy/dα = cosec² (5π/6) = (1/sin (5π/6)² = (1/ (1/2)² = 2² = 4.
New answer posted
3 months agoContributor-Level 10
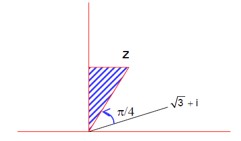
Given Re (z-1)/ (2z+i) = 1, where z = x + iy.
(z-1)/ (2z+i) = [ (x-1) + iy] / [2x + I (2y+1)]
To rationalize, multiply the numerator and denominator by the conjugate of the denominator [2x - I (2y+1)].
Numerator = [ (x-1) + iy] * [2x - I (2y+1)] = 2x (x-1) - I (x-1) (2y+1) + i2xy + y (2y+1)
Real part of the numerator = 2x (x-1) + y (2y+1).
Denominator = (2x)² + (2y+1)².
Re (z-1)/ (2z+i) = [2x (x-1) + y (2y+1)] / [ (2x)² + (2y+1)²] = 1.
2x² - 2x + 2y² + y = 4x² + 4y² + 4y + 1.
0 = 2x² + 2y² + 2x + 3y + 1.
So, 2x² + 2y² + 2x + 3y + 1 = 0.
New answer posted
3 months agoContributor-Level 10
. Let the terms in Arithmetic Progression be a – 2d, a – d, a, a + d, a + 2d.
Sum of terms: (a – 2d) + (a – d) + a + (a + d) + (a + 2d) = 5a.
5a = 25 ⇒ a = 5.
Product of terms: (5 – 2d) (5 – d) (5) (5 + d) (5 + 2d) = 2520.
5 (25 – 4d²) (25 – d²) = 2520.
(25 – 4d²) (25 – d²) = 504.
625 – 25d² – 100d² + 4d? = 504.
4d? – 125d² + 121 = 0.
Factoring the equation: (4d² - 121) (d² - 1) = 0.
So, d² = 1 or d² = 121/4.
d = ±1 or d = ±11/2.
If d = ±1, the terms are 3, 4, 5, 6, 7.
If d = ±11/2, the terms are -6, -1/2, 5, 21/2, 16.
The largest term is 5 + 2d = 5 + 2 (11/2) = 5 + 11 = 16.
New answer posted
3 months agoContributor-Level 10
Given 2ae = 6 and 2a/e = 12.
From these, ae = 3 and a/e = 6.
Multiplying the two equations: (ae) (a/e) = 3 * 6 => a² = 18.
We know that b² = a² (1 - e²) = a² - a²e² = 18 - (ae)² = 18 - 3² = 18 - 9 = 9.
The length of the latus rectum (L.R.) is 2b²/a.
L.R. = 2 * 9 / √18 = 18 / (3√2) = 6/√2 = 3√2.
New answer posted
3 months ago
Contributor-Level 10
1st observation: n? =10, mean x? =2, variance σ? ²=2.
Σx? = n? x? = 20.
σ? ² = (Σx? ² / n? ) - x? ² => 2 = (Σx? ²/10) - 2² => 6 = Σx? ²/10 => Σx? ² = 60.
2nd observation: n? , mean y? =3, variance σ? ²=1. Let n? =n.
Σy? = ny? = 3n.
σ? ² = (Σy? ² / n) - y? ² => 1 = (Σy? ²/n) - 3² => 10 = Σy? ²/n => Σy? ² = 10n.
Combined variance σ² = 17/9. n_total = 10+n.
Combined mean = (Σx? +Σy? )/ (10+n) = (20+3n)/ (10+n).
Combined Σ (squares) = 60+10n.
σ² = (Combined Σsq / n_total) - (Combined mean)²
17/9 = (60+10n)/ (10+n) - [ (20+3n)/ (10+n)]²
Multiply by 9 (10+n)²:
17 (10+n)² = 9 (60+10n) (10+n) - 9 (20+3n)²
17 (100+
New answer posted
3 months agoContributor-Level 10
1/16, a, b are in GP. So, a² = b/16 .
Also, a, b, 1/6 are in AP. So, 2b = a + 1/6.
From the first equation, b = 16a².
Substitute into the second: 2 (16a²) = a + 1/6 => 32a² - a - 1/6 = 0.
192a² - 6a - 1 = 0.
The solution appears to solve a different problem.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers