Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
Mass m will acquire velocity 2u. Total momentum of system will be conserved but total kinetic energy is not conserved during collision.
New answer posted
4 months agoContributor-Level 10
Correctly identifying isotopes and isobars requires knowing both the atomic and mass numbers. Relying on only one is a common error.
- Isotopes: Same element (atomic number), different mass.
- Isobars: Different elements (atomic number), same mass.
New answer posted
4 months agoContributor-Level 10
Rutherford's atomic model was a breakthrough, but it was flawed. It couldn't explain atomic stability, as orbiting electrons should lose energy and spiral into the nucleus. It also failed to account for the discrete line spectra observed from excited atoms.
New answer posted
4 months agoContributor-Level 10
Let sin x = t, t
Minimum value of a for which solution exist = 9
New answer posted
4 months agoContributor-Level 10
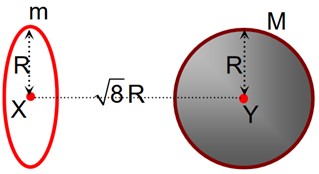
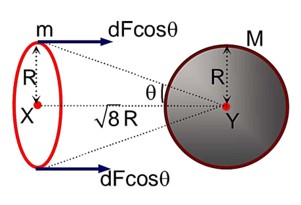
all i = 1, 2, 3
Case 1 7 one's and two zeroes which can occur in 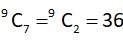
Case 2 One 2 three 1's five zeroes =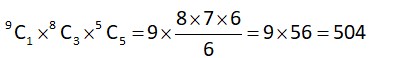
total such matrices = 504 + 36 = 540
New answer posted
4 months agoContributor-Level 10
Equation of normal is 4x – 3y + 1 = 0
Equation of tangent is 3x + 4y – 43 = 0
Area of triangle =

Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers