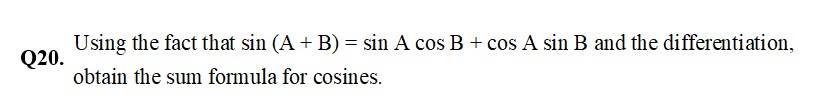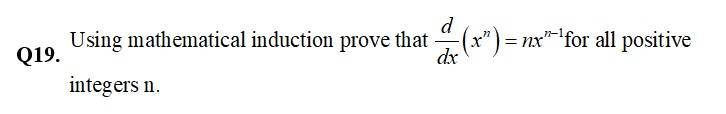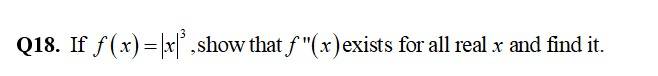Class 12th

The given D.E. is

$x\frac{dy}{dx}+2y=x^{2}logx$

$\Rightarrow \frac{dy}{dx}+\frac{2}{x}.y=xlogx$ which is of form $\frac{dy}{dx}+Py=Q$

So, $P=\frac{2}{x}\&Q=xlogx$

$\therefore I.F=e^{{\displaystyle \int Pdx}}=e^{{\displaystyle \int \frac{2}{x}dx}}=e^{2logx}=e^{log{x}^2}=x^2$

Thus, the general solution is of the form.

$y*x^2={\displaystyle \int xlogx.x^{2}dx+c}$

$={\displaystyle \int logx}{x}^{3}dx+c$

$\begin{array}{l}=logx{\displaystyle \int x^{3}dx-{\displaystyle \int \frac{d}{dx}logx{\displaystyle \int x^{3}dxdx+c}}}\\ =\frac{logx.x^4}{4}-{\displaystyle \int \frac{1}{4}*\frac{x^4}{4}dx+c}\end{array}$

$\begin{array}{l}=y{x}^2=\frac{x^4}{4}logx-\frac{x^4}{16}+c\\ =y=\frac{x^2}{4}logx-\frac{x^2}{16}+\frac{c}{x^2}\end{array}$

137. Yes, Let us take $f(x)=|x-1|+|x-2|.$

So, x = 1, x= 2 divides the real line into three disjoint intervals $(-\infty ,1],[1,2]$ and $[2,\infty ).$

For $x\in (-\infty ,1].$

$f(x)=-(x-1)+[-(x-2)]=-x+1-x+2=3-2x.$

For $x\in [1,2].$

$f(x)=(x-1)-(x-2)=1.$

For $x\in [2,\infty )$

$f(x)=x-1+x-2=2x-3.$

Hence, these polynomial fun are all continous and desirable. for all real values of x or, except x = 1 and x = 2.

ie, $\forall x\in R-\{1,2\}.$

For differentiavity at x = 1,

LHD = $=\underset{x\to 1^{-}}{lim}\frac{f(x)-f(1)}{x-1}=\underset{x\to 1^{-}}{lim}\frac{3-2x-1}{x-1}=\underset{x\to 1^{-}}{lim}\frac{2-2x}{x-1}.$

$=\underset{x\to 1^{-}}{lim}\frac{-2(x-1)}{x-1}$

$=\underset{x\to 1^{-}}{lim}-2$

= -2

RHD = $=\underset{x\to 1^{+}}{lim}\frac{f(x)-f(1)}{x-1}=\underset{x\to 1^{+}}{lim}\frac{1-1}{x-1}=\underset{x\to 1^{+}}{lim}\frac{0}{x-1}=0.$

as L.HD ≠ R.HD

f is not differentiable at x =1.

For continuity at x = 1.

L.HL= $=\underset{x\to 1^{-}}{lim}f(x)=\underset{x\to 1^{-}}{lim}=1.$

RHL = $\underset{x\to 1^{+}}{lim}f(x)=\underset{x\to 1^{+}}{lim}1=1$ \ LHL = RHS

f is continuous at x = 1

For continuity & differentiability at x = 2

$=\underset{x\to 2^{-}}{lim}f(x)=\underset{x\to 2^{-}}{lim}1=1.$

$=\underset{x\to 2^{+}}{lim}f(x)=\underset{x\to 2^{+}}{lim}(2x-3)=4-3=1.$

? LHL = RHL

f is continuous at x = 2

$\begin{array}{l}=\underset{x\to 2^{-}}{lim}\frac{f(x)-f(2)}{x-2}=\underset{x\to 2^{-}}{lim}\frac{1-1}{x-2}=\underset{x\to 2^{-}}{lim}=\frac{0}{x-2}\\ \end{array}$

$=\underset{x\to 2^{+}}{lim}\frac{f(x)-f(2)}{x-2}=\underset{x\to 2^{+}}{lim}\frac{2x-3-1}{x-2}$

$=\underset{x\to 2^{+}}{lim}\frac{2(x-2)}{x-2}$

$=\underset{x\to 2^{+}}{lim}2$

= 2

? LHD ≠ RHD

f is not differentiable at x = 2.

The given D.E.is

$\begin{array}{l}co{s}^{2}x\frac{dy}{dx}+y=tanx\\ =\frac{dy}{dx}+\frac{1}{co{s}^{2}x}y=\frac{tanx}{co{s}^{2}x}\end{array}$

$=\frac{dy}{dx}+se{c}^{2}xy=se{c}^{2}xtanx$ Which is of form $\frac{dy}{dx}+Py=Q$

So, $P=se{c}^{2}x\&Q=se{c}^{2}xtanx$

$\therefore I.F=e^{{\displaystyle \int Pdx}}=e^{{\displaystyle \int se{c}^{2}dx}}=e^{tanx}$

Thus, the general solution is of the form.

$y.e^{tanx}={\displaystyle \int se{c}^{2}xtanx.}{e}^{tanx}dx+c$

Let, $tanx=t=se{c}^{2}xdx=dt$

$\begin{array}{l}=y{e}^t={\displaystyle \int t.}{e}^{t}dt+c\\ =t{\displaystyle \int e^{t}dt-{\displaystyle \int \frac{d}{dt}t{\displaystyle \int e^{t}dt.dt+c}}}\\ =t{e}^t-{\displaystyle \int e^{t}dt+c}\\ =t{e}^t-e^t+c\\ =e^t\left(t-1\right)+c\end{array}$

$\begin{array}{l}\Rightarrow y{e}^{tanx}=e^{tanx}\left(tanx-1\right)+c\\ y=\left(tanx-1\right)+c{e}^{-tanx}\end{array}$

9. In FeO crystal, some of the Fe²⁺ ions are replaced by Fe³⁺ ions i.e., 3Fe²⁺ ions are replaced by 2Fe³⁺ ions to make up for the loss of positive charge. As a result of which it leads to lesser amount of metal as compared to the stoichiometric proportion.

136. Given, $sin(A+B)=sinAcosB+cosAsinB$

Differentiating w r t. 'x' we get,

$\frac{d}{dx}sin(A+B)=\frac{d}{dx}(sinAcosB+cosAsinB)$

$\to cos(A+B)-\frac{d}{dx}(A+B)=sinA\frac{d}{dx}cosB+cosB\frac{d}{dx}sinA+cosA\frac{d}{dx}sinB+sinB\frac{d}{dx}cosA$

$\to cos(A+B)\left(\frac{dA}{dx}+\frac{dB}{dx}\right)=-sinAsinB\frac{dB}{dx}+cosBcosA\frac{dA}{dx}+cosAcosB\frac{dB}{dx}-sinAsinB\frac{dA}{dx}$

$\to cos(A+B)\left(\frac{dA}{dx}+\frac{dB}{dt}\right)=cosAcosB\left(\frac{dA}{dx}+\frac{dB}{dx}\right)-sinAsinB\left(\frac{dA}{dx}+\frac{dB}{dx}\right)$

$=(cosAcosB-sinAsinB)\left(\frac{dA}{dx}+\frac{dB}{dx}\right).$

$\to cos(A+B)=cosAcosB-sinAsinB.$

The given D.E.is

$\frac{dy}{dx}+\left(secx\right)y=tanx$ Which is in the form $\frac{dy}{dx}+Py=Q$

So, $P=secx\&Q=tanx$

$\therefore$ $\therefore I.F=e^{{\displaystyle \int Pdx}}=e^{{\displaystyle \int secxdx}}=e^{log\left|secx+tanx\right|}=secx+tanx$

Thus, the general solution is ,

$\begin{array}{l}y*I.F={\displaystyle \int Q*I.Fdx+c}\\ =y*\left(secx+tanx\right)={\displaystyle \int tanx}\left(secx+tanx\right)dx+c\end{array}$

$\begin{array}{l}={\displaystyle \int \left(tanxsecx+ta{n}^{2}x\right)dx+c}\\ ={\displaystyle \int \left(tanxsecx+se{c}^2-1\right)}dx+c\\ =sec+tanx-x+c\end{array}$

$=\left(secx+tanx\right)y=secx+tanx-x+c\left\{?se{c}^{2}x=ta{n}^{2}x+1\right\}$

8. Yellow colour in NaCl is due to the defect called as metal excess defect. In this defect anionic vacancies get created due to the diffusion of Cl-ions to the surface of the crystal and there after unpaired electrons occupy anionic sites. These sites are known as F-centres. The electrons at F-centres then absorb energy from the visible region and undergo excitation which makes the crystal appear yellow.

The given D.E. is

$\frac{dy}{dx}+\frac{y}{x}=x^2$ Which is in the form $\frac{dy}{dx}+Py=Q$

So,  $P=\frac{1}{x}=\&Q=x^2$

$\therefore I.F=e^{{\displaystyle \int Pdx}}=e^{{\displaystyle \int \frac{1}{2}dx}}=e^{logx}=x\left\{?e^{logx}=x\right\}$

Thus, the general solution is

$\begin{array}{l}y*I.F={\displaystyle \int Q*I.Fdx+c}\\ y.x={\displaystyle \int x^2.xdx+c}\\ =xy={\displaystyle \int x^{3}dx+c}\\ =xy=\frac{x^4}{4}+c\end{array}$

7. Crystals have long range ordered arrangement of  their constituent particles but usually these crystals are not perfect as during the process of crystallisation some deviations as compared to such ideal arrangement set in depending upon the rate of cooling or presence of impurities in solution  also this process occurs at such a rate that the constituent particles may not get the sufficient time to arrange themselves in a perfect order  and hence these deviations or irregularities in arrangement is being termed as defects or imperfections. Therefore, crystals are usually not perfect. 

135. Given, $f(x)=|x{|}^3=\{\begin{array}{cc}\hfill x^3\hfill & \hfill if x\ge 0\hfill \\ \hfill -x^3\hfill & \hfill if x<0\hfill \end{array}$

For $x\ge 0,f(x)=|x{|}^3=x^3$

and $\begin{array}{cc}\hfill f^{\prime }(x)=3x^2\hfill & \hfill f^{\prime \prime }(x)=6x\hfill \end{array}$

For $x<0,f(x)=|x{|}^3={(-x)}^3=-x^3.$

so, $\begin{array}{cc}\hfill f^{\prime }(x)=-3x^2\hfill & \hfill f^{\prime \prime }(x)=-6x\hfill \end{array}$

Hence, $f^{\prime \prime }(x)=\{\begin{array}{cc}\hfill 6x,\hfill & \hfill if x\ge 0\hfill \\ \hfill -6x,\hfill & \hfill if x<0\hfill \end{array}$