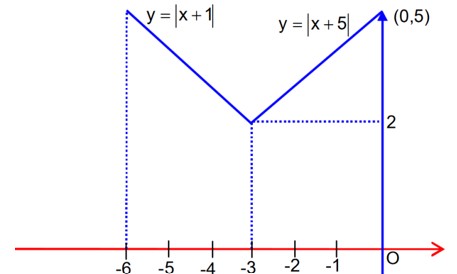
Class 12th

Each element of ordered pair (i, j) is either present in A or in B.

              So, A + B = Sum of all elements of all ordered pairs {i, j} for $1\le i\le 10$ and $1\le j\le 10$  

              = 20 (1 + 2 + 3 + … + 10) = 1100

$l=\frac{48}{{\pi }^4}{\displaystyle {\int }_0^{\pi }\left[{\left(\frac{\pi }{2}-x\right)}^3-\frac{3{\pi }^2}{4}\left(\frac{\pi }{2}-x\right)+\frac{{\pi }^3}{4}\right]\frac{sinxdx}{1+co{s}^{2}x}}$

Using ${\displaystyle {\int }_a^{b}f\left(x\right)dx={\displaystyle {\int }_a^{b}f\left(a+b-x\right)dx}}$

we get $l=\frac{48}{{\pi }^4}{\displaystyle {\int }_0^{\pi }\left[-{\left(\frac{\pi }{2}-x\right)}^3+\frac{3{\pi }^2}{4}\left(\frac{\pi }{2}-x\right)+\frac{{\pi }^3}{4}\right]\frac{sinxdx}{1+co{s}^{2}x}}$

Adding these two equations, we get

$\Rightarrow l=\frac{12}{\pi }{\left[-ta{n}^{-1}\left(cosx\right)\right]}_0^{\pi }=\frac{12}{\pi }.\frac{\pi }{2}=6$

Sum of all elements of $A\cap B=2$   [Sum of natural number upto 100 which are neither divisible by 3 nor by 5]

$=2\left[\frac{100*101}{2}-3\left(\frac{33*34}{2}\right)-5\left(\frac{20*21}{2}\right)+15\left(\frac{6*7}{2}\right)\right]$

= 10100 – 3366 – 2100 + 630

              = 5264

$\left(sin10°.sin50°.sin70°\right).\left(sin10°.sin20°.sin40°\right)$

$=\left(\frac{1}{4}sin30°\right).\left[\frac{1}{2}sin10°\left(cos20°-cos60°\right)\right]$

$=\frac{1}{32}\left[sin30°-sin10°-sin10°\right]$

$\frac{1}{64}-\frac{1}{16}sin10°$

Clearly $\alpha =\frac{1}{64}$  

              Hence 16 + a^-1 = 80

$\left(4+x^2\right)dy-2x\left(x^2+3y+4\right)dx=0$

$\Rightarrow \frac{dy}{dx}=\left(\frac{6x}{x^2+4}\right)y+2x$

$e^{-3\mathcal{l}n\left(x^2+4\right)}=\frac{1}{{\left(x^2+4\right)}^3}$

so $\frac{y}{{\left(x^2+4\right)}^3}={\displaystyle \int \frac{2x}{{\left(x^2+4\right)}^3}dx+c}$

$\Rightarrow y=-\frac{1}{2}\left(x^2+4\right)+c{\left(x^2+4\right)}^3$

When x = 0, y = 0 gives $c=\frac{1}{32}$

So, for x = 2, y = 12

$\therefore {\displaystyle \underset{-6}{\overset{0}{\int }}f\left(x\right)dx=2*\frac{1}{2}\left(2+5\right)*3=21}$

  ${E^o}_{Cell}={E^o}_{A{g}^{+}/Ag}-{E^o}_{Z{n}^{+2}/Zn}=0.8+0.76=1.56V$

Anode :  $Zn\left(s\right)\to Z{n}^{2+}\left(aq\right)+2e^{-}$    

Cathode :  2Ag⁺(aq) + 2e^- -> 2Ag(s)

Zn(s) + 2Ag⁺(aq) -> Zn²⁺ (aq) + 2Ag(s)

  $E_{cell}={E^o}_{Cell}-\frac{0.0591}{n}log\frac{\left[Z{n}^{2+}\right]}{{\left[A{g}^{+}\right]}^2}=1.56-\frac{0.0591}{2}log\left(\frac{0.1}{10^{-4}}\right)$          

x = 147

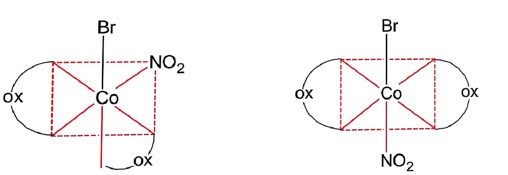
Cis (optically active)                          Trans (optically inactive)

d & l form (2)                                                    (1)

So, total 3 isomerism.

$f\left(x\right)=2co{s}^{-1}x+4co{t}^{-1}x-3x^2-2x+10\forall x\in \left[-1,1\right]$

$\Rightarrow f\text{'}\left(x\right)=-\frac{2}{\sqrt[]{1-x^2}}-\frac{4}{1+x^2}-6x-2<0\forall x\in \left[-1,1\right]$

So, f (x) is decreasing function and range of f (x) is

$\left[f\left(1\right),f\left(-1\right)\right],$ which is $\left[\pi +5,5\pi +9\right]$

Now 4a – b = 4 (p + 5) - (5p + 9) = 11 - “π”

$f\left(x\right)=a{x}^2+bx+c$  

g (x) = px + q

  $f\left(g\left(x\right)\right)=a{\left(px+q\right)}^2+b\left(p\right)\left(+q\right)+c$

$?8x^2?2x=a{\left(px+q\right)}^2+b\left(px+q\right)+c$

Compare 8 = ap² …………… (i)

-2 = a (2pq) + bp

0 = aq² + bq + c

  $9\left(f\left(x\right)\right)=p\left(a{x}^2+bx+c\right)+q$

=>4x² + 6x + 1 = apx² + bpx + cp + q

=> Andhra Pradesh = 4 ……………. (ii)

6 = bp

1 = cp + q

From (i) & (ii), p = 2, q = -1

=> b = 3, c = 1, a = 2

f (x) = 2x² + 3x + 1

f (2) = 8 + 6 + 1 = 15

g (x) = 2x – 1

g (2) = 3