- Introduction to Three Dimensional Geometry Short Answer Type Questions
- Introduction to Three Dimensional Geometry Long Answer Type Questions
- Introduction to Three Dimensional Geometry Objective Type Questions
- Introduction to Three Dimensional Geometry Fill in the blank Type Questions
- Introduction to Three Dimensional Geometry Matching Type Questions
- JEE Mains 2021
Introduction to Three Dimensional Geometry Short Answer Type Questions
| Locate the following points: i. (1, –1, 3), ii. (–1, 2, 4) iii. (–2, –4, –7), iv. (–4, 2, –5). |
| Sol.
|
| Name the octant in which each of the following points lies: i. (1, 2, 3), ii. (4, –2, 3), iii. (4, –2, –5), iv. (4, 2, –5), v. (–4, 2, 5), vi. (–3, –1, 6), vii. (2, –4, –7), viii. (–4, 2, –5). |
| Sol:
|
Commonly asked questions
Show that if , then the point is at a distance of 1 unit from the origin.
This is a short answer type question as classified in NCERT Exemplar
Name the octant in which each of the following points lies:
i. (1, 2, 3),
ii. (4, –2, 3),
iii. (4, –2, –5),
iv. (4, 2, –5),
v. (–4, 2, 5),
vi. (–3, –1, 6),
vii. (2, –4, –7),
viii. (–4, 2, –5).
This is a short answer type question as classified in NCERT Exemplar
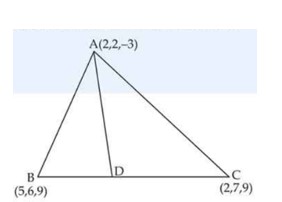
Let be the feet of perpendiculars from a point on the -, -, and -axes, respectively. Find the coordinates of in each of the following where the point is:
i. A = (3, 4, 2),
ii. (–5, 3, 7),
iii. (4, –3, –5).
This is a short answer type question as classified in NCERT Exemplar
Let be the feet of perpendiculars from a point on the -, -, and -planes, respectively. Find the coordinates of in each of the following where the point is:
i. (3, 4, 5),
ii. (–5, 3, 7)
iii. (4, –3, –5).
This is a short answer type question as classified in NCERT Exemplar
How far apart are the points (2, 0, 0) and (–3, 0, 0)?
This is a short answer type question as classified in NCERT Exemplar
Find the distance from the origin to (6, 6, 7).
This is a short answer type question as classified in NCERT Exemplar
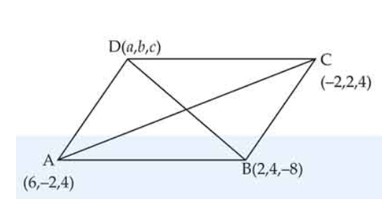
Three consecutive vertices of a parallelogram are , , and . Find the coordinates of the fourth vertex.
[Hint: Diagonals of a parallelogram have the same mid-point.]
This is a short answer type question as classified in NCERT Exemplar
Show that the triangle with vertices , , and is right angled.
This is a short answer type question as classified in NCERT Exemplar
Find the third vertex of a triangle whose centroid is the origin and two vertices are and .
This is a short answer type question as classified in NCERT Exemplar
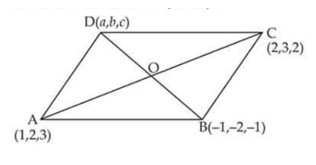
Three vertices of a parallelogram are , , and . Find the fourth vertex .
This is a short answer type question as classified in NCERT Exemplar
Find the coordinates of the points which trisect the line segment joining the points and .
This is a short answer type question as classified in NCERT Exemplar
If the origin is the centroid of a triangle having vertices , , and , find the values of .
This is a short answer type question as classified in NCERT Exemplar
Locate the following points:
i. (1, –1, 3),
ii. (–1, 2, 4)
iii. (–2, –4, –7),
iv. (–4, 2, –5).
This is a short answer type question as classified in NCERT Exemplar
Show that the points , , and are collinear.
This is a short answer type question as classified in NCERT Exemplar
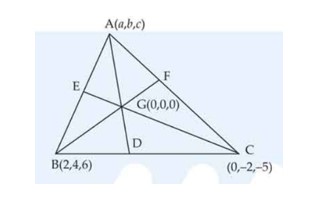
Let , , and be the vertices of a triangle. The internal bisector of angle meets at the point . Find the coordinates of .
This is a short answer type question as classified in NCERT Exemplar
If for some q, q, r R, not at all have same sign, one of the roots of the equation is also a root of the equation x2 + 2x – 8 = 0, then is equal to………….
Let a and b are the roots of
Also, it has a common root with x2 + 2x – 8 = 0
The common root between above two equations is 4.
The number of 5-digit natural numbers, such that the product of their digits is 36, is……
Factors of 36 = 22.32.1
Five-digit combinations can be
(1, 2, 3, 3), (1, 4, 3, 1), (1, 9, 2, 1), (1, 4, 9, 11), (1, 2, 3, 6, 1), (1, 6, 1, 1)
i.e., total numbers
The series of positive multiples of 3 is divided into sets : Then the sum of the elements in the 11th set is equal to…………..
Given series
Also up to 10th set total 3 × k type terms will be 1 + 3 + 5 + ……… +19 = 100 terms
Sum of elements = 3 × (101 + 102 + ….+121)
The number of distinct real roots of the equation x5 + is …………..
are roots of above equation and x5 + 3x – 1 is a monotonic term hence vanishes at exactly one value of x other then 1 or -1.
3 real roots.
If the coefficients of x and x2 in the expansion of (1 + x)p (1 – x)q, p, q 15, are -3 and -5 respectively, then the coefficient of x3 is equal to…………………
Coefficient of x in
Coefficient of x2 in
Coefficient of x3 in
If dx, then n ![]() N is equal to
N is equal to
using by parts we get
Let a cure y = y(x) pass through the point (3, 3) and the area of the origin under this curve, above the x-axis and between the abscissae 3 and x (>3) be . If the curve also passes through the point in the first quadrant, then a is equal to………….
differentiating w.r.to x
After solving we get also curve passes through (3, 3) Þ c = -2
which passes through
The equations of the sides AB, BC and CA of a triangle ABC are 2x + y = 0, x + py = 15a and x – y = 3 respectively. If its orthocenter is (2, a), then p is equal to…………
Slope of AH = slope of BC =
slope of HC =
slope of BC × slope of HC = -1 Þ p = 3 or 5
hence p = 3 is only possible value.
Let the function f(x) = 2x2 – loge x, x > 0, be decreasing in (0, a) and increasing in (a, 4). A tangent to the parabola y2 = 4ax at a point P on it passes through the point (8a, 8a – 1) but does not pass through the point If the equation of the normal at P is then a + b is equal to…………….
so f (x) is decreasing in
Tangent at y2 = 2x is y = mx + it is passing through (4, 3) therefore we get m =
So tangent may be passes through (-2, 0) so rejected.
Equation of normal
Let Q and R be two points on the line at a distance from the point P(4, 2, 7). Then the surface of the area of the triangle PQR is……………
Let PT perpendicular to QR
therefore
Therefore square of = 153.
Introduction to Three Dimensional Geometry Long Answer Type Questions
| 1. Show that the three points , , and are collinear and find the ratio in which divides . |
| Sol:
|
| 2. Prove that the points , , and are collinear. Find the ratio in which the first point divides the join of the other two. |
Commonly asked questions
Show that the three points , , and are collinear and find the ratio in which divides .
This is a short answer type question as classified in NCERT Exemplar
Prove that the points , , and are collinear. Find the ratio in which the first point divides the join of the other two.
This is a long answer type question as classified in NCERT Exemplar
What are the coordinates of the vertices of a cube whose edge is 2 units, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?
This is a long answer type question as classified in NCERT Exemplar
Introduction to Three Dimensional Geometry Objective Type Questions
| 1. The distance of point from the -plane is (a) 3 units (b) 4 units (c) 5 units (d) 550 |
| Sol.
|
| 2. What is the length of the foot of the perpendicular drawn from the point on the -axis? (a) (b) (c) 5 (d) None of these |
| Sol. |
Commonly asked questions
The distance of point from the -plane is
(a) 3 units
(b) 4 units
(c) 5 units
(d) 550
This is an Objective Type Questions as classified in NCERT Exemplar
What is the length of the foot of the perpendicular drawn from the point on the -axis?
(a)
(b)
(c) 5
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
Distance of the point from the origin is
(a)
(b) 3
(c) 4
(d) 5
This is an Objective Type Questions as classified in NCERT Exemplar
If the distance between the points and is , then the value of is
(a) 5
(b)
(c) –5
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
-axis is the intersection of two planes
(a) and
(b) and
(c) and
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
Equation of -axis is considered as
(a)
(b)
(c)
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
The point lies in the
(a) First octant
(b) Seventh octant
(c) Second octant
(d) Eighth octant
This is an Objective Type Questions as classified in NCERT Exemplar
A plane is parallel to yz-plane so it is perpendicular to:
(a) x -axis
(b) y-axis
(c) z-axis
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
The locus of a point for which is
(a) Equation of x-axis
(b) Equation of y-axis
(c) Equation of z-axis
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
The locus of a point for which is
(a) -plane
(b) -plane
(c) -plane
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
If a parallelepiped is formed by planes drawn through the points and parallel to the coordinate planes, then the length of the diagonal of the parallelepiped is
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
is the foot of the perpendicular drawn from a point on the -plane. The coordinates of point are
(a)
(b)
(c)
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
is the foot of the perpendicular drawn from a point on the -axis. The coordinates of are
(a)
(b)
(c)
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
Introduction to Three Dimensional Geometry Fill in the blank Type Questions
| 1. The three axes determine ____. |
| Sol:
|
| 2. The three planes determine a rectangular parallelepiped which has ____ rectangular faces. |
| Sol:
|
Commonly asked questions
The three axes determine ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
A line is parallel to -plane if all the points on the line have equal ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If the midpoints of the sides of a triangle are , then the centroid of the triangle is ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The three planes determine a rectangular parallelepiped which has ____ rectangular faces.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The coordinates of a point are the perpendicular distances from the ____ on the respective axes.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The three coordinate planes divide the space into ____ parts.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If a point P lies in the yz-plane, then the coordinates of the point on the yz-plane are of the form ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The equation of yz-plane is ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If the point lies on the -axis, then the coordinates of are of the form ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The equation of -axis is ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
A line is parallel to -axis if all the points on the line have equal ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
represents a plane parallel to ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The plane parallel to -plane is perpendicular to ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
The length of the longest piece of string that can be stretched straight in a rectangular room whose dimensions are 10, 13, and 8 units is ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
If the distance between the points and is 5, then ____.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Introduction to Three Dimensional Geometry Matching Type Questions
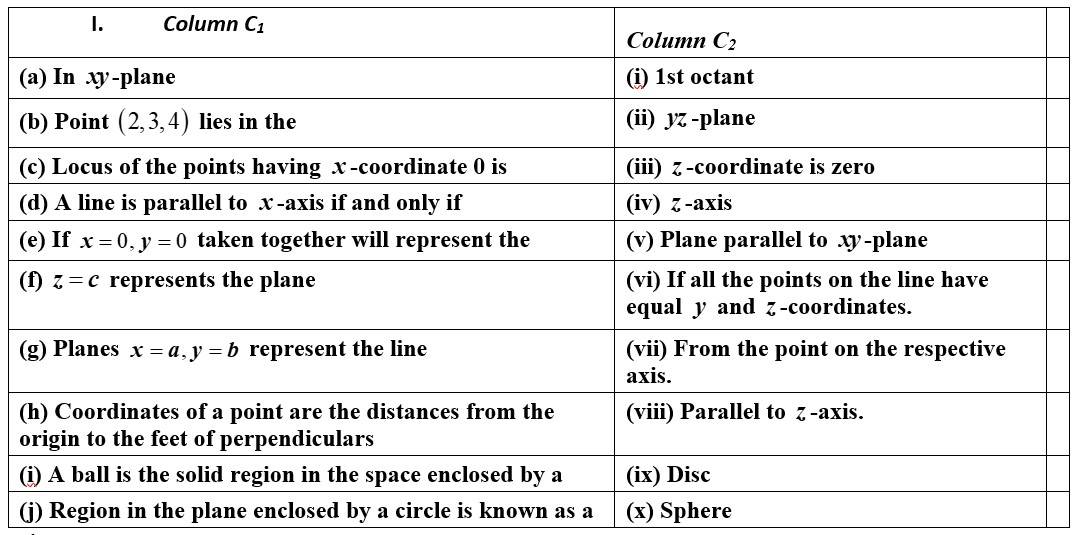
| Match each item given under Column C1 to its correct answer given under Column C2: |
| Sol. |
Commonly asked questions
Match each item given under Column C1 to its correct answer given under Column C2:
This is a matching answer type question as classified in NCERT Exemplar
JEE Mains 2021
JEE Mains 2021
Maths NCERT Exemplar Solutions Class 11th Chapter Twelve Exam