Physics Current Electricity

${\text{?}\mathrm{}}_{\mathrm{s}}\stackrel{?}{\mathrm{B}}\cdot \mathrm{d}\stackrel{?}{\mathrm{A}}=0\mathrm{}$ (No monopole exist)

For conductors α $\alpha$  is (+ve)

For semiconductors $\alpha$  is (-ve)

$\mathrm{R}=22*{10}^3\pm 5\mathrm{\%}$ First band  Red

2nd band $=$  Red

3rd band =Orange (Multiplier)

4th band = Gold (Tolerance)

R_eq = (R? )/ (R? +R? ) ⇒ p (l)/ (2A) = [ (p? l/A) (p? l/A)] / [ (p? l/A) + (p? l/A)]

⇒ ρ/2 = (p? )/ (p? +p? ) ⇒ ρ = (2p? p? )/ (p? +p? ) = (2 * 6 * 3)/9 = 4 Ωcm

12/x = 6/ (72-x) ⇒ x = 144 - 2x ⇒ x = 144/3 = 48cm

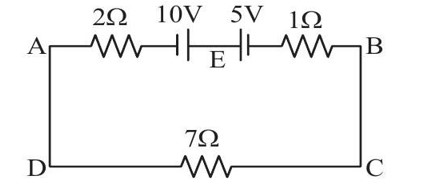
R_eq = 10 + (50 * 20) / (50 + 20) = 170/7 Ω
⇒ I = 170 / (170/7) = 7A
⇒ x = 10 * 7 = 70V ⇒ Voltage across 10Ω resistor

Conduction current density, J? = E/ρ = (V/d) / ρ = (V? sin (2πft) / (pd)
Displacement current density, J? = ε (dE/dt) = (ε/d) (dV/dt) = (2πfε/d) * V? cos (2πft)
The ratio of their magnitudes is:
J? / J? = tan (2πft) / (2πfε? ρ) = tan (2π * 900) / (2π * 9 * 10? * 80ε? * 0.25) = 10?

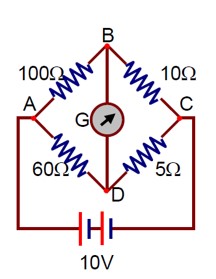
Let V? = 10V, V? = xV, V? = 0V, and V? = yV.
Applying Kirchhoff's current law at node B:
(x - 10)/100 + (x - y)/15 + (x - 0)/10 = 0 ⇒ 53x - 20y = 30 . (1)
Applying Kirchhoff's current law at node D:
(y - 10)/60 + (y - x)/15 + (y - 0)/5 = 0 ⇒ 17y - 4x = 10 . (2)
Solving equations (1) and (2), we get:
x = 0.865 and y = 0.792
The current i? is:
i? = (x - y) / 15 = 4.87 mA

From ohm's Law, V = IR = I (ρl / A) = I (ρl / (πd²/4) ⇒ ρ = (πd²V) / (4lI)
Relative error in resistivity,
Δρ/ρ = 2 (Δd/d) + ΔV/V + Δl/l + ΔI/I = 2 * (0.01/5.00) + (0.1/5.0) + (0.1/10.0) + (0.01/2000) = 0.039
Percentage error = (Δρ/ρ) * 100 = 3.9%

For series combination: s = R? + R?

For parallel combination: p = (R? ) / (R? + R? )

Given the condition s = np:
R? + R? = n * (R? ) / (R? + R? )
(R? + R? )² = nR? R?
R? ² + 2R? R? + R? ² = nR? R?
R? ² - 2R? R? + R? ² + 4R? R? = nR? R?
(R? - R? )² = (n - 4)R?
(R? - R? )² / (R? ) = n - 4
n = 4 + (R? - R? )² / (R? )

Since (R? - R? )² is always non-negative, the minimum value of the term (R? - R? )² / (R? ) is 0. This occurs when R? = R?
Therefore, the minimum value of n is 4.