Physics Motion in Plane
Get insights from 107 questions on Physics Motion in Plane, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Motion in Plane
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
3 months agoContributor-Level 10
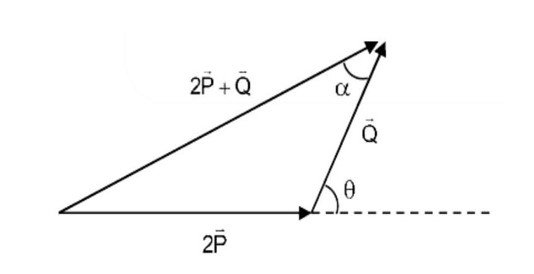
The graphical method using the head-to-tail or parallelogram laws only helps in visualising vectors and their resultants. But, it has limited accuracy. Because they cannot be precise when you consider the scale and angles. That's why it is important to use vector addition using the analytical method. That involves combining vector components. The graphical approach is primarily for conceptual understanding.
New answer posted
3 months agoContributor-Level 10
Scalar quantities only have magnitude, which makes sense to combine using ordinary algebra. But vector quantities have both magnitude and direction. Due to this directional aspect, vectors must obey special rules of vector algebra. Vectors have to specifically follow the triangle law or the parallelogram law of addition to be represented in the graph format. These graphical methods account for both magnitude and direction. This makes sure that the resultant vector accurately reflects the combined effect of the individual vectors. If we apply ordinary algebra, we won't be able to know the directional information.
New answer posted
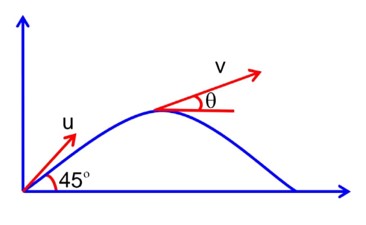
3 months agoContributor-Level 10
First angle, θ1 = θ,
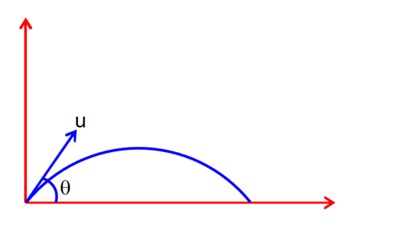
Another angle (θ2 = 90 - θ) for which range will be
Same as that of θ1 = θ
at
So, Both statement is true & Reason is correct explanation for statement 1.
New answer posted
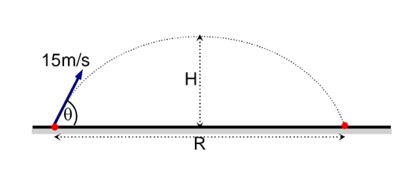
3 months agoContributor-Level 10
We know that horizontal speed will remain constant
20 cos = v cos ……… (i)
Along y-axis
……. (ii)
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers