physics ncert solutions class 11th
Get insights from 952 questions on physics ncert solutions class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about physics ncert solutions class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
5 months agoContributor-Level 10
Length of the pipe, l = 20 cm = 0.2 m
Source frequency = normal mode frequency is given by the relation
= (2n-1) , n is an integer = 0,1,2,3, ….
430 = (2n-1)
n = 1
Hence, the first mode of vibration frequency is resonantly excited by the given source. In a pipe open at both ends, the mode of vibration frequency is given by the relation:
, n = = = 0.5
Since the number of the node of vibration (n) has to be an integer, the given source does not produce a resound vibration in an open pipe.
New answer posted
5 months agoContributor-Level 10
Length of the steel rod, l = 100 cm = 1 m
Fundamental frequency of vibration, = 2.53 kHz = 2.53 Hz
When the rod is plucked at its middle, an antinode (A) is formed at the centre, and the nodes (N) are formed at its two ends, as shown in the figure.
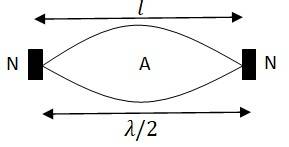
The distance between two successive nodes is
l = = 2l = 2 m
The speed of sound in steel is given by the relation
v = = 2.53 = 5.06 m/s = 5.06 km/s
New answer posted
5 months agoContributor-Level 10
Frequency of the tuning fork, = 340 Hz
Since the given pipe is attached with a piston at one end, it will behave as a pipe with one end closed and the other end open, as shown in this figure.
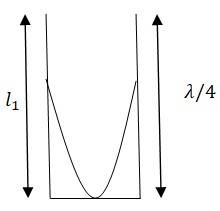
= of the pipe = 25.5 cm = 0.255 m
= 4 m = 1.02 m
The speed of sound is given by the relation, v = = 340 = 346.8 m/s
New answer posted
5 months agoContributor-Level 10
Mass of the wire, m = 3.5 kg
Linear mass density, = 4 kg/m
Frequency of vibration, = 45 Hz
Length of the wire, l = = = 0.875 m
The wavelength of the stationary wave = , where n = number of nodes in the wire
For fundamental node, n = 1, = 2l = 2
(a) The speed of the transverse wave in the string is given as v = = 45 = 78.75 m/s
(b) The tension produced in the string is given by the relation, T = = 4 = 248.06 N
New answer posted
5 months agoContributor-Level 10
(a) The given equation represents a stationary wave because the harmonic terms kx and appear separately in the equation.
(b) The given equation does not contain any harmonic term. Therefore, it does not represent either a travelling wave or a stationary wave.
(c) The given equation represents a travelling wave as the harmonic terms kx and are in the combination of kx – .
(d) The given equation represents a stationary wave because the harmonic terms kx and in the equation. This equation represents the superposition of two stationary waves.
New answer posted
5 months agoContributor-Level 10
(i)
(a) All the points on the string oscillates with the same frequency, except at the nodes, which have zero frequency
(b) All the points in any vibrating loop have the same phase, except at the nodes.
(c) All the points in any vibrating loop will have different amplitudes of vibration.
(ii)
The given equation is: y (x, t) = 0.06 sin ( cos (120
For x = 0.375 and t =0
Amplitude = Displacement = 0.06 sin ( cos (0 = 0.06sin ( = 0.042 m
New answer posted
5 months agoContributor-Level 10
(a) The general equation representing a stationary wave is given by the displacement function y(x,t) = 2asin kx cos
The equation is similar to the give equation y(x, t) = 0.06 sin ( cos (120
Hence, the given function represents a stationary wave.
A wave travelling along the positive x-direction is given as: = asin ( t – kx)
The wave travelling along the negative x-direction is given as: = asin ( t + kx)
(b) The superposition of these two waves yields:
y = = asin ( t – kx) + asin ( t + kx)
= a sin( t)cos(kx) – a sin(kx)cos(&nbs
New answer posted
5 months agoContributor-Level 10
The equation for a travelling harmonic wave is given by
y(x, t) = 2.0 cos 2 (10t – 0.0080 x + 0.35) or
= 2.0 cos (20 t – 0.016 x + 0.70 )
Comparing with classical equation y (x, t) = a , we get
Amplitude a = 2.0 cm. Propagation constant, k = 0.016 , angular frequent,
From the relation
(a) For x = 4 m = 400 cm, we have = 0.016 = 6.4 rad
(b) For x = 0.5 m = 50 cm, we have = 0.016 = 0.8 rad
(c) For x = , we have = rad
(d) For x = , we have &nbs
New answer posted
5 months agoContributor-Level 10
All the waves have different phases. The given transverse harmonic wave is:
y(x, t) = 3.0 sin (36t + 0.018x + ) ………(i)
For x = 0, the equation reduces to
y (0,t) = 3.0 sin (36t + )
Also = , so T = = = s
For plotting y vs., t graphs using different values of t, we get
When t = 0, y = 2.12
t = = , y = 3
t = = , y = 2.12
t = = , y = 0
t = = , y = -2.12
t = = , y = -3
t = = , y = -2.12
t = = , y = 0
For x = 2 and x = 4.
New answer posted
5 months agoContributor-Level 10
The equation of a progressive wave travelling from right to left is given by the displacement function:
y (x, t) = a ……….(i)
The given equation is
y(x, t) = 3.0 sin (36 t + 0.018 x + /4) …….(ii)
On comparing equations (i) and (ii), we find that the equation (ii) represents a travelling wave, propagating from right to left. Now, using equations (i) and (ii), we can write
, k = 0.018
From the relation and and v = , we can write
v = = = = 2000 cm /s = 20 m/s
Hence, the speed of the given travelling wave is 20 m/s
The frequency &
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 686k Reviews
- 1800k Answers
