Structure of Atoms
Get insights from 148 questions on Structure of Atoms, answered by students, alumni, and experts. You may also ask and answer any question you like about Structure of Atoms
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
6 months agoContributor-Level 10
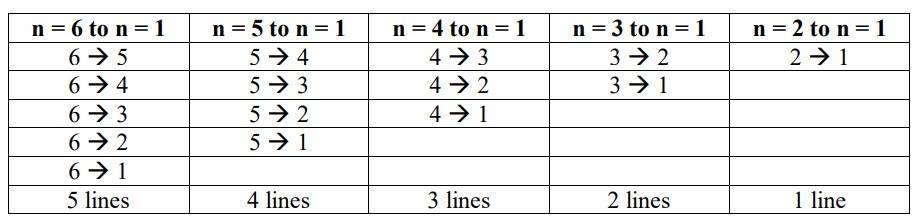
The maximum no. of emission lines = [n (n–1)] /2 = [6 (6–1)] / 2 =3 * 5 = 15
The transitions that take place are as follows:
New answer posted
6 months agoContributor-Level 10
Energy of a hydrogen present in a particular energy shell,
En = 13.12 x 105 / n2 J mol-1 = (13.12 x 105) / (n2 x 6. 022 x 1023) J atom-1
= -2.18 x 10-18 / n2 J atom-1
Step I: Ionisation energy for hydrogen electron present in orbit n = 5
IE5 = E∞ - E5 = 0 – [ (-2.18 x 10-18) / 25] J atom-1 = 8.72 x 10-20 J atom-1
Step II: Ionisation energy for hydrogen electron present in orbit n = 1
IE1 = E∞ - E1 = 0 – [ (-2.18 x 10-18) / 1] J atom-1 = 2.18 x 10-18 J atom-1
Therefore IE1 / IE5 = (2.18 x 10-18 J atom-1) / (8.72 x 10-20 J atom-1) = 25
The energy required to remove an electron from first orbit in a hydrogen atom is 25 times the energy n
New answer posted
6 months agoContributor-Level 10
According to Balmer formula,
Wave number (? ) = RH [1/n12 - 1/n22 ]cm-1
= 109678 [1/22 – 1/42] cm-1
= (109678 x 3) / 16 cm-1
λ = 1 /? = 16 / (109678 x 3) cm = 16 x 107 / (109678 x 3) nm = 486 nm
New answer posted
6 months agoContributor-Level 10
Threshold frequency (v0) = c /λ = (3 * 108 m s-1) / (68 x 10-8 m) = 4.41 x 1014 s-1
Work function (W0) = hv0 = (6.626 * 10-34 Js) x (4.41 x 1014 s-1) = 2.92 x 10-19 J.
New answer posted
6 months agoContributor-Level 10
Energy of one photon (E) = hc / λ
= (6.626 * 10-34 Js) x (3 * 108 m s-1) / (0.57 * 10-6 m) = 3.48 x 10-19 J
Rate of emission of quanta per second = Power / Energy = (25 watt) / (3.48 x 10-19 J)
= (25 Js-1) / (3.48 x 10-19 J) = 7.18 x 1019 s-1
New answer posted
6 months agoContributor-Level 10
Given: λ = 242 nm = 142 x 10-9 m, c = 3 x 108 ms-1, h = 6.626 x 10-34Js
We know, E = hc / λ
= (6.626 * 10-34 Js) x (3 * 108 m s-1) / (242 * 10-9 m) = 0.0821 x 10-17 J
∴ Ionization energy per mol (E) = (0.0821 x 10-17 J) x (6.022 x 1023 mol-1J) / 1000 = 494 kJ mol-1
New answer posted
6 months agoContributor-Level 10
(i) Energy of photon (E) = hc / λ
= (6.626 * 10-34 Js) x (3 * 108 m s-1) / (4 * 10-7 m) = 4.969 x 10-19 J
Since, 1.6020 * 10-19 J= 1 eV
So, 1 J= (1 eV) / (1.6020 * 10-19 J)
Hence, 4.969 x 10-19 J = (1eV) x (4.969 x 10-19 J) / (1.602 x 10-19 J) = 3.1 eV
(ii) Kinetic energy of emission = Energy – work function
= (3.1 – 2.13) = 0.97 eV
(iii) Kinetic energy of emission = 0.97 eV
=> ½ mv2= 0.97 eV = 0.97 x 1.602 x 10-19 J = 0.97 x 1.602 x 10-19 kg m2 s-2
=> v2 = (2 x 0.97 x 1.602 x 10-19 kg m2 s-2 ) / (9.1 x 10-31 kg) = 0.34 x 1012 m2 s-2
=> v = (0.34 x 1012 m2 s-2)1/2 = 0.583 x 106 ms-1 = 5.83 x 105 ms-1
New answer posted
6 months agoContributor-Level 10
Given: h = 6.626 * 10-34 Js,
c = 3 * 108 m s-1,
λ = 4000 pm = 4000 * 10-12 m = 4 * 10-9 m
Energy of photon (E) = hc / λ
= (6.626 * 10-34 Js) x (3 * 108 m s-1) / (4 * 10-9 m) = 4.969 x 10-17 J
i.e. 4.969 x 10-17 J is the energy of 1 photon
Therefore, 1 J is the energy of photons = 1 / (4.969 x 10-17) = 2.012 x 1016 photons.
New question posted
6 months agoTaking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers