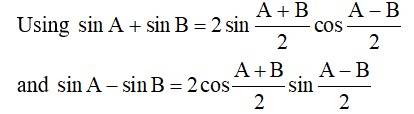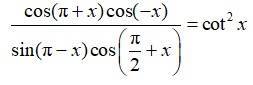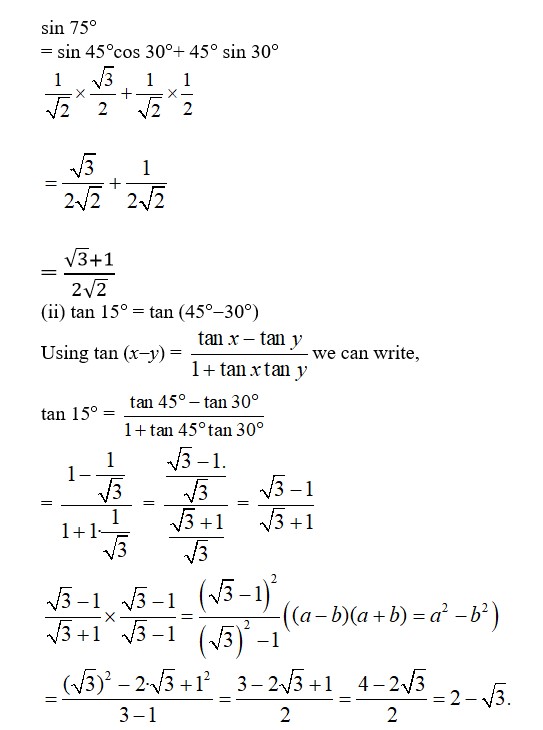Trigonometric Functions
Get insights from 128 questions on Trigonometric Functions, answered by students, alumni, and experts. You may also ask and answer any question you like about Trigonometric Functions
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
31. L.H.S. = sin 2x + 2 sin 4x + sin 6x
Using sin A + sin B = 2 sin A + B/2 cos A - B/2 we have,
L.H.S. = (sin 2x + sin 6x) + 2 sin 4x
We know that,
Hence,
L.H.S
= R.H.S
New answer posted
7 months agoContributor-Level 10
30. L.H.S
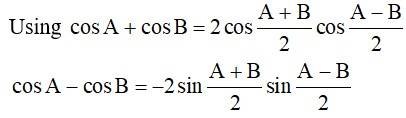
As sin 2θ = 2 sinθ cosθ.
L.H.S. = sin (2*4x) sin(2*2x)
= sin 8x sin 4x
= R.H.S.
New answer posted
7 months agoContributor-Level 10
L.H.S =
Using cos (A + B) = cos A cos B – sin A sin B
and cos (A – B) = cos A cos B + sin A sin B
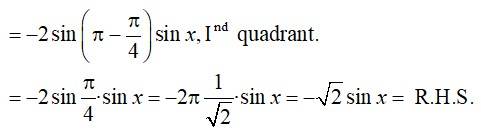
New answer posted
7 months agoContributor-Level 10
27. L.H.S
Let A = (n+1)x and B = (n+2)x
So, L.H.S = cosAcosB + sin Asin B
Putting values of A and B we get,
L.H.S =
R.H.S
New question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
23. (i) sin 75°= sin (45°+30°)
Using sin (x + y)= sin x cos y + cos x sin y we can write
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers