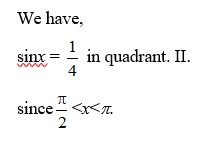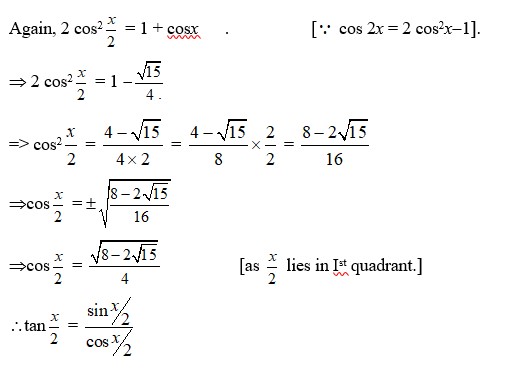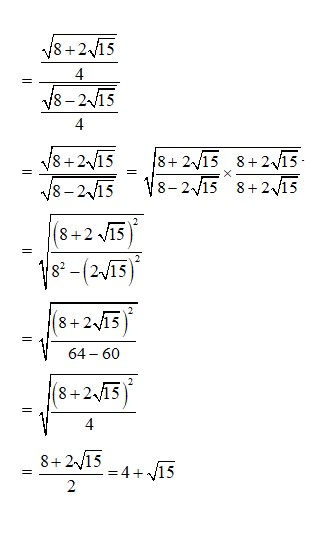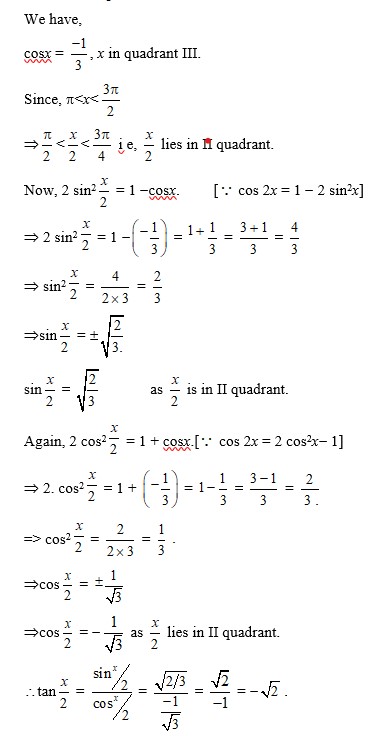Trigonometric Functions
Get insights from 128 questions on Trigonometric Functions, answered by students, alumni, and experts. You may also ask and answer any question you like about Trigonometric Functions
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New question posted
7 months agoNew answer posted
7 months agoContributor-Level 10
59. We have, tan x= , x in IInd quadrant.
Since,
sin , cos , tan are all positive.
Now, sec2x = 1 + tan2x = 1 + = 1 + = =
secx = ±
cosx = ± .
cosx = as x is in IInd quadrant.
Now, 2 sin2. = 1 cosx. [cos 2x = 1 2 sin2x.]
2 sin2 = 1
2 sin2 = 1 += = .
sin2 = =

New answer posted
7 months agoContributor-Level 10
58. L.H.S = sin 3x + sin 2x - sin x
= sin 3x - sin x + sin 2x.
= 2 cos . sin + sin 2x
= 2 cos sin + sin 2x.
= 2 cos 2x sin x + 2 sin xcosx [ sin 2x = 2sin xcosx]
= 2 sin x [cos 2x + cosx]
= 2 sin x
= 2 sin x
= 4 sin xcos . cos = R.H.S.
New answer posted
7 months agoContributor-Level 10
57. L.H.S. =
Using sin A + sin B = 2 sin cos
cos A + cos B = 2 cos cos

New answer posted
7 months agoContributor-Level 10
56. L.H.S = sin x + sin 3x + sin 5x + sin 7x.
= (sin x + sin 7x) + (sin 3x + sin 5x)
Using,
sin A + sin B = 2 sin cos
L.H.S. = 2. Sin cos + 2 sin cos
= 2 sin cos + 2 sin cos
= 2 sin 4x cos 3x + 2 sin 4x cosx.[ cos (-x) = cosx]
= 2 sin 4x[cos 3x + cosx]
Using cos A + cos B = 2 cos cos
So, L.H.S. = 2 sin 4x
= 2 sin 4x
= 4 sin 4x. cos 2x cosx = R.H.S.
New answer posted
7 months agoContributor-Level 10
55. L.H.S = (cos x-cos y)2 + (sin x- sin y)2
=
= 4 sin2 sin2 + 4 cos2 sin2
= 4 sin2
= 4 . [ sin2∅ + cos2∅= 1]
= R.H.S.
New answer posted
7 months agoContributor-Level 10
54. L.H.S. = (cos x + cos y)2 + (sin x- sin y)2
Using,
cos A + cos B = 2 cos cos
sin A - sin B = 2 cos sin
L.H.S. = .
= 4. cos2 cos2 . + 4 cos2 sin2 .
= 4 cos2
= 4 cos2 [ cos2θ+ sin2qθ = 1].
= R.H.S.
New answer posted
7 months agoContributor-Level 10
53. L.H.S = (sin 3x + sin x) + sin x + (cos 3x - cosx) cosx.
Using
Sin A + sin B = 2 sin cos
cos A - cos B = -2 sin sin .
L.H.S. = sin x + cosx
= 2 sin cos sin x -2 sin sin cosx.
= 2 sin 2xcosx sin x -2 sin 2x sin xcosx
= 0 = R.H.S.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers