Class 11th

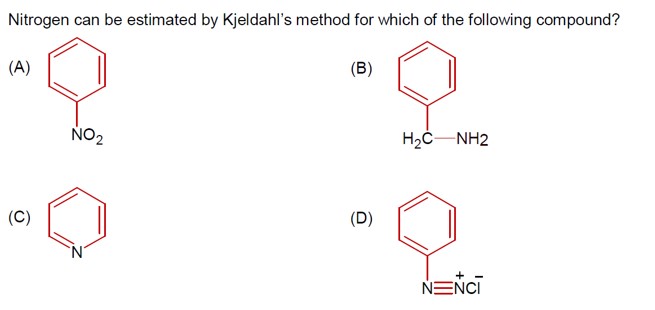
The Kjeldahl method is not applicable for nitrogen estimation in:

Compounds containing nitrogen in a nitro group.

Compounds containing an Azo group.

Pyridine.

Initial mean of 25 observations is 40.
X? = (Σx? )/25 = 40 => Σx? = 25 * 40 = 1000.

A teacher of age 60 retires.
The new sum of ages for the remaining 24 people is 1000 - 60 = 940.

A new teacher of age x joins.
The new sum for 25 people is 940 + x.
The new mean is 39.
(940 + x) / 25 = 39
940 + x = 39 * 25 = 975
x = 975 - 940 = 35.
The new teacher's age is 35.

Sucralose: Artificial sweetener

Glyceryl ester of stearic acid: The document incorrectly identifies this as "Sodium stearate which is synthetic detergent". Sodium stearate is a soap, not a synthetic detergent.

Sodium benzoate: Food preservative

Bithionol: Antiseptic

Please consider the following Image

Given the equation y = 3 + 1/ (4 + 1/y).
y - 3 = 1 / (4y+1)/y)
y - 3 = y / (4y+1)
(y-3) (4y+1) = y
4y² + y - 12y - 3 = y
4y² - 11y - 3 = y
4y² - 12y - 3 = 0

Using the quadratic formula to solve for y:
y = [-b ± √ (b²-4ac)] / 2a
y = [12 ± √ (-12)² - 4*4* (-3)] / (2*4)
y = [12 ± √ (144 + 48)] / 8
y = [12 ± √192] / 8 = [12 ± 8√3] / 8 = 3/2 ± √3.
y = 1.5 ± √3.

Since y > 0 (from the structure of the equation), both solutions are positive. The solution selects y = 1.5 + √3.

Evaluate the limit:
L = lim (x→0) [sin? ¹ (x) - tan? ¹ (x)] / 3x³

Using Taylor series expansions around x=0:
sin? ¹ (x) = x + x³/6 + O (x? )
tan? ¹ (x) = x - x³/3 + O (x? )

L = lim (x→0) [ (x + x³/6) - (x - x³/3) ] / 3x³
L = lim (x→0) [ x³/6 + x³/3 ] / 3x³
L = lim (x→0) [ (1/6 + 1/3)x³ ] / 3x³
L = (1/2) / 3 = 1/6

The solution shows 3L = 1/2, which is correct. And 6L = 1, also correct.
The final line 6L+1=2 implies 6L=1, confirming the result.

Given the determinant:
| α β γ |
| β γ α | = 0
| γ α β |

The expansion of this determinant is - (α³ + β³ + γ³ - 3αβγ) = 0.
This implies (α+β+γ) (α²+β²+γ²-αβ-βγ-γα) = 0.

From a cubic equation x³ + ax² + bx + c = 0 with roots α, β, γ:
α+β+γ = -a
αβ+βγ+γα = b
αβγ = -c

Substituting into the determinant condition:
(-a) ( (α+β+γ)² - 3 (αβ+βγ+γα) ) = 0
(-a) ( (-a)² - 3b ) = 0
-a (a² - 3b) = 0
a (a² - 3b) = 0

This implies a=0 or a²=3b. If a≠0, then a²=3b, so a²/b = 3.

Given the family of parabolas y² = 4a (x+a).
Differentiate with respect to x:
2y (dy/dx) = 4a
a = (y/2) (dy/dx)

Substitute a back into the original equation:
y² = 4 * (y/2) (dy/dx) * [x + (y/2) (dy/dx)]
y² = 2y (dy/dx) * [x + (y/2) (dy/dx)]
y = 2 (dy/dx) * [x + (y/2) (dy/dx)]
y = 2x (dy/dx) + y (dy/dx)²
y (dy/dx)² + 2x (dy/dx) - y = 0