Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
2 months agoContributor-Level 10
To find the sum Σ[r=0 to 6] (?C?)².
This is the coefficient of x? in the expansion of (1+x)?(x+1)? = (1+x)¹².
By the binomial theorem, (1+x)¹² = Σ[k=0 to 12] ¹²C? x?.
The coefficient of x? is ¹²C?.
¹²C? = (12 * 11 * 10 * 9 * 8 * 7) / (6 * 5 * 4 * 3 * 2 * 1) = 11 * 2 * 3 * 2 * 7 = 924.
New answer posted
2 months agoContributor-Level 10
g? = g - ω²R ⇒ 0 = g - ω²R ⇒ ω = √ (g/R)
⇒ T = 2π/ω = 2π√ (R/g) = 2 * 3.14 * √ (6400 * 10³)/10)
New answer posted
2 months agoContributor-Level 10
I = ∫[0 to 10] [sin(2πx)] / e^(x-[x]) dx.
The period of the integrand involves [sin(2πx)] which depends on the sign of sin(2πx) and {x} = x - [x], which has a period of 1.
Let f(x) = [sin(2πx)] / e^{x}.
The integral is ∫[0 to 10] f(x) dx = 10 * ∫[0 to 1] f(x) dx due to the periodicity of {x} and the integer period of sin(2πx).
In the interval (0, 1/2), sin(2πx) is between 0 and 1, so [sin(2πx)] = 0.
In the interval (1/2, 1), sin(2πx) is between -1 and 0, so [sin(2πx)] = -1.
At x=0, 1/2, 1, the value is 0.
So, ∫[0 to 1] f(x) dx = ∫[0 to 1/2] 0 dx + ∫[1/2 to 1] -1/e^x dx
= 0 + [-e^(-x) * (-1)] from 1/2 to 1 = [e^(-x)] from 1
New answer posted
2 months agoContributor-Level 10
(A) sin (ωt) + cos (ωt) = √2 sin (ωt + π/4) ⇒ T = 2π/ω
(B) sin² (ωt) = 1/2 - (1/2)cos (2ωt) ⇒ T = 2π/ (2ω) = π/ω
(C) 3cos (π/4 - 2ωt) ⇒ T = 2π/ (2ω) = π/ω
(D) cos (ωt) + cos (2ωt) + cos (3ωt)
Time period of cos (ωt) = 2π/ω
Time period of cos (2ωt) = 2π/ (2ω)
Time period of cos (3ωt) = 2π/ (3ω)
Time period of combined function = 2π/ω
New answer posted
2 months agoContributor-Level 10
A = Area swept ⇒ dA/dt = (1/2)r² (dθ/dt) = (1/2) (Mr²ω)/M = L / (2M)
New answer posted
2 months agoContributor-Level 10
Parabola: y² = 4x - 20 = 4(x - 5). Vertex at (5,0).
Line: The text seems to derive the tangent equation y = x - 4. This is not a tangent to the given parabola. The standard tangent to y²=4aX is Y=mX+a/m. Here X=x-5, a=1. So y = m(x-5)+1/m.
The other curve is an ellipse: x²/a² + y²/b² = 1.
The text says x²/2 + (x-4)²/b² = 1. This assumes a² = 2.
x²/2 + (x²-8x+16)/b² = 1
x²(1/2 + 1/b²) - (8/b²)x + (16/b² - 1) = 0.
For tangency, the discriminant (D) of this quadratic equation must be zero.
D = (8/b²)² - 4(1/2 + 1/b²)(16/b² - 1) = 0.
64/b? - 4(8/b² - 1/2 + 16/b? - 1/b²) = 0.
16/b? - (7/b² - 1/2 + 16/b?) = 0.
-7/b² + 1/2 = 0
New answer posted
2 months agoContributor-Level 10
PV? = C ⇒ V? (dP/dV) + P (γV^ (γ-1) = 0 ⇒ dP/dV = -γ (P/V) ⇒ dP/P = -γ (dV/V)
New answer posted
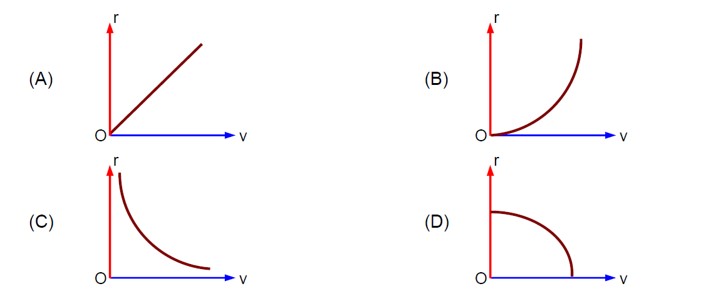
2 months ago
Contributor-Level 10
U = mV (r) = -Cm/r
F = -dU/dr = -Cm/r² ⇒ The force which provides required centripetal force
⇒ mv²/r = Cm/r² ⇒ r = C/v²
New answer posted
2 months ago
Contributor-Level 10
(v/v? ) + (x/x? ) = 1 ⇒ v = - (v? /x? )x + v?
⇒ a = dv/dt = - (v? /x? ) (v) = - (v? /x? ) [- (v? /x? )x + v? ] ⇒ a = (v? ²/x? ²)x - v? ²/x?
- Concept involved: Graph of kinematics
- Topic: Kinematics
- Difficulty level: Moderate
- Note: IIT-Jee-2005
- Point of Error: Writing Equation of straight line and differentiation
New answer posted
2 months agoContributor-Level 10
Limit (θ→0) [tan(πcos²θ) / sin(2πsin²θ)]
Let θ → 0. Then cos²θ → 1 and sin²θ → 0.
Let u = πsin²θ. As θ → 0, u → 0.
cos²θ = 1 - sin²θ = 1 - u/π.
The expression becomes:
Limit (u→0) [tan(π(1 - u/π)) / sin(2u)]
= Limit (u→0) [tan(π - u) / sin(2u)]
= Limit (u→0) [-tan(u) / sin(2u)]
= Limit (u→0) [-tan(u) / (2sin(u)cos(u))]
= Limit (u→0) [-(sin(u)/cos(u)) / (2sin(u)cos(u))]
= Limit (u→0) [-1 / (2cos²(u))] = -1 / (2 * 1²) = -1/2.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 65k Colleges
- 1.2k Exams
- 679k Reviews
- 1800k Answers