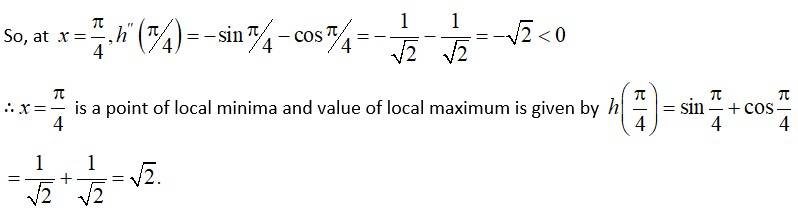Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
(i) we have, f(x) = x2.
f(x) = 2x.
andf(x) = 2.
AR extreme point, f(x) = 0
2x = 0
x = 0.
When x = 0, f(0) = 2 > 0.
∴x = 0 is a point of local minima and value of local minimum is given by f(0) = 02 = 0.
(ii) g(x) = x3 3x
A(ii)
we have, g(x) = x3- 3x
g'(x) = 3x2- 3
g''(x) = 6x.
At extreme point,
g'(x) = 0
3x2- 3 = 0.
3(x2- 1) = 0 ⇒ 3(x - 1)(x + 1) = 0.
x = 1 or x = -1.
At x = 1, g"(1) = 6.1 = 6 > 0.
So, x = 1 is a point of local minima and value of local minimum is given by g(1) = 13- 3.1 = 1 - 3 = - 2.
And at x = -1, g"( -1) = 6 ( -1) = 6 < 0.
So, x = -1 is a point of local minima and value of local minimum is given by
g(- 1) = (- 1)3- 3(- 1) = 1 + 3 = 2.
New answer posted
7 months agoContributor-Level 10
(i) we have, f(x) = |x + 2| - 1
We know that, for all
f(x)- 1.
∴ Minimum value of f(x) = -1 when x + 2 = 0 x = - 2.
And maximum value of f(x) does not exist.
(ii)
A(ii)
We have,
For all
g(x) 3.
∴ Maximum value of g(x) = 3 when
And minimum value does not exist.
(iii) h(x) = sin (2x) + 5.
A(iii)
we have, h(x) = sin (2x) + 5.
For all {range of sine function is [-1, 1]}
-1 + 5 sin 2x + 5 1 + 5.
4 h(x) 6.
∴ Maximum value of h(x) = 6.
Minimum value of h(x) = 4.
(iv)
A(iv)
we have,
As for all
-1 + 3 sin 4x + 3 1 + 3
2 f(x) 4.
∴ Maximum value of f(x) = 4.
Minimum value of f(x) = 2.
(
New answer posted
7 months agoContributor-Level 10
(i) We have, f(x) = (2x - 1)2 + 3.
For all
(2x - 1)2 + 3 ≥ 3.
f(x) ≥ 3.
∴The minimum value of f(x) = 3. When 2x - 1 = 0--> x =
Again as as there is vouppa bound to 'x' value hence, f(x) has no maximum values.
(ii)
A(ii)
We have, f(x) = 92 + 12x + 2.
(Taking 9 common from each team).
For all
f(x)≥ - 2.
∴The minimum value of f(x) = -2 when
And as so f(x) has
no maximum values.
(iii) f(x) = (x - 1)2 + 10
A(iii)
we have, f(x) = - (x - 1)2 + 10
For all
(x - 1)2 ≤ 0
-(x- 1)2 + 10 ≤ 10.
f(x) ≤ 10.
∴maximum value of f(x) = 10 when x - 1 = 0 x = 1.
And minimum value of f(x) does n
New answer posted
7 months agoContributor-Level 10
The volume v of a cube with side 'x' metre is v = x3
So,
∴increase in side, Δx = 3% of =
∴dv = 3x2π
Hence, option (C) is correct.
New answer posted
7 months agoContributor-Level 10
We have, y = f (x) = 3x2 + 15x + 5.
dy = (6x + 15) dx
Δy = (6x + 15) Δx.
Let, x = 3 and Δx = 0.02 then,
Δy = f (x + Δx) - f (x)
f (x + Δx) = f (x) + Δy = f (x) + (6x + 5) Δx.
f (3 + 0.02) = 3 (3)2 + 15 (3) + 5 + (6 * 3 + 15) (0.02).
f (3.02) = 27 + 45 + 5 + (18 + 15) (0.02).
= 77 + 0.66
= 77.66
∴ Option (D) is correct.
New answer posted
7 months agoContributor-Level 10
Let be the radius of the sphere &r be the error in measuring the radius.
Then, π = 9m and Δr = 0.03m.
Now, surface area S of the sphere is
S = 4πr2
So,
∴e, this = Δr = 8πr.Δr = 8π * 9 * 0.03
= 2.16πm3.
Appropriate error in calculating the surface area is 2.16πm3.
New answer posted
7 months agoContributor-Level 10
Let x be the radius of the sphere & Δπ be the error in measuring the radius.
Then, π = 7m and Δr = 0.02m.
Now, volume v of sphere is
So,
dv = 4π (7)2 (.0.02) = 3.92 πm3
∴The appropriate error is calculating the volume is 3.92πm3.
New answer posted
7 months agoContributor-Level 10
We know that, the surface area 5 of a 'x' when length cube, is S = 6x2.
So,
Given decrease in side,
New answer posted
7 months agoContributor-Level 10
We know that, the volume v of side 'a' mete of cube is v = x3.
So,
Given that, increase in side = 1% of x.
New answer posted
7 months agoContributor-Level 10
Given, y = f (x) = x3- 7x2 + 15.
So,
dy = (3x2- 14x) dx.
Δy = (3x2- 14x) Δx.
Let, x = 5 and Δx = 0.001. Then,
Δy = f (x + Δx) f (x).
f (x + Δx) = f (x) + Δy = f (x) + (3x2- 4x) Δx.
f (5 + 0.001) = 53- 7 (5)2 + 15 + [3 (5)2 - 14 (5)]. (0.001).
f (5.001) = 125 - 175 + 15 + (75 - 70) (0.001)
= -35 + 0.005 = - 34.995.
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers