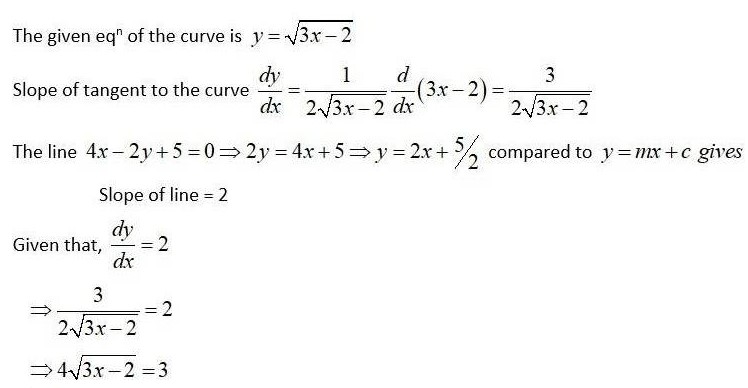Tags Class 12th

Class 12th

Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th

Follow Ask Question

12k

Questions

Discussions

Active Users

Followers

New answer posted

7 months ago

Class 12th Application of Derivatives

66. Find the approximate value of f(2.01), where f (x) = 4x² + 5x + 2.

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

Given, y = f (x) = 4x² + 5x + 2.

So, f (x) = 8x + 5. $\frac{d y}{d x}$ = 8x + 5 dy = (8x + 5) dx.

Let x = 2 and Δx = 0.01.Then,

f (x + Δx) = f (2 + 0.01) = f (2.01).

Δy = f. (x + Δx) f (Δx).

f (x +Δx) = f (x) +Δy.

= f (x) + dy = f (x) + (8x + 5) dx.

= f (2.01) = f (2) + (8 x 2 + 5). Δx {∴dx = Δx}

= 4 (2)² + 5 (2) + 2 + 21 (0.01)

= 16 + 10 + 2 + 0.21 = 28.21.

0 0

New answer posted

7 months ago

Class 12th Application of Derivatives

65. Using differentials, find the approximate value of each of the following up to 3 places of decimal.

0 Follower 6 Views

Vishal Baghel

Contributor-Level 10

(i) Let y= ?x : Let x = 25 and x = 0. 3.

Then, ?y = ?x+?x $?x$

$=?25.3 ?25$

$=?25.3 ? 5$

$?25.3 = 5 + ? y ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? y ~ d y .$

= 5 + dy

= $5 + (\frac{d y}{d x}) A x .$

$= 5 + \frac{1}{2?x} ? x .$

$= 5 + \frac{1}{2?25} ? 0.3$

$= 5 + \frac{0.3}{2 * 5}$

= 5 + 0.03

$?25.3 = 5.030$

(ii) ?49.5

A.(ii)

Let y = ?x $.$ Let x = 49 and x = 0.5.

Then, $? y =?x+?x ?x .$

$=?49.5 ?49$

$?49.5 = 7 + ? y = 7 + {(\frac{d y}{d x})}_{}^{? x}$

$= 7 + \frac{1}{2?x} ? x$

$= 7 + \frac{1}{2?49} * (0.5)$

$= 7 + \frac{0.5}{14}$

= 7 + 0.0357.

$?49.5 = 7 ? 035$

(iii) ?0.6

A.(iii)

Let y = ?x $.$ Let x = 0.64 and ?x = 0.04.

Then, $? y =?x+Ax ?x$

$=?0.64-0.04 ?0.64 .$

$=?0.6 ? 0.8$

$?0.6= 0.8 + ? y = 0.8 + (\frac{d y}{d x}) ? x$

$= 0.8 + \frac{1}{2?x} ? x$

$= 0.8 + \frac{1}{2?0.64} * (? ? 0.04)$

$= 0.8 \frac{? 0.04}{2 * 0.8}$

= 0.8 - 0.025.

= 0.775.

(iv) ${(0.009)}^{\frac{1}{3}}$

A.(iv)

Let $y = x^{\frac{1}{3}}$ Let x = 0.008 and ?x = 0.00 1.

Then, ?y = ${[x + ? x]}^{\frac{1}{3}} ? {[x]}^{\frac{1}{3}}$

$= {(0.009)}^{\frac{1}{3}} ? {(0.008)}^{\frac{1}{3}}$

${(0.009)}^{\frac{1}{3}} = 0.2 + ? y = 0.2 + \frac{d y}{d x} ? ? x$

$= 0.2 + \frac{1}{3 {(x^{\frac{1}{3}})}^{2}} ? x$

$= 0.2 + \frac{1}{3 {[{(0.008)}^{\frac{1}{3}}]}^{2}} * (0.001)$

$= 0.2 + \frac{0.001}{3 * {(0.0)}^{2}} = 0.2 + \frac{0.001}{0.12}$

= 0.2 + 0.0083.

= 0.208.

(v) ${(0.999)}^{\frac{1}{10}}$

A.(v)

Let $y = x^{\frac{1}{10}} .$ Let x = 1 and ?x = -0.001

Then, $? y = {(x + ? x)}^{\frac{1}{10}} ? x^{\frac{1}{10}}$

$= {(0.999)}^{\frac{1}{10}} ? {(1)}^{\frac{1}{10}}$

$? 1 {(0.999)}^{\frac{1}{10}} = 1 + A y$

$= 1 + \frac{d y}{d x} ? x .$

$= 1 + \frac{1}{10 x^{\frac{9}{10}}} * ? x$

$= 1 ? \frac{0.001}{10 (. 1^{\frac{9}{10}})} = 1 ? \frac{0.001}{10} = 1 ? 0.0001$

= 0.999.

(vi) ${(15)}^{\frac{1}{4}}$

A.(vi)

Let $y = x^{\frac{1}{4}} .$ Then, x = 16 and ?x = 1.

Then, $? y = {(x + A x)}^{\frac{1}{4}} ? x^{\frac{1}{4}} .$

$= {(15)}^{\frac{1}{4}} ? {(16)}^{\frac{1}{4}}$

$? {(15)}^{\frac{1}{4}} = 2 + A y = 2 + \frac{d y}{d x} A x$

$= 2 + \frac{1}{4 x^{\frac{3}{4}}} ? (? 1)$

$= 4 ? \frac{1}{4 {(16)}^{\frac{3}{4}}}$

$= 2 ? \frac{1}{4 * 8}$

$= 4 ? \frac{1}{32}$

$= \frac{64 ? 1}{32} = \frac{63}{32} = 1.968$

(vii) ${(26)}^{\frac{1}{3}}$

A.(vii)

Let $y = x^{\frac{1}{3}} .$ Let x = 27 and ?x = 1.

Then, $? y = {(x + ? x)}^{\frac{1}{3}} ? x^{\frac{1}{3}}$

$= {(26)}^{\frac{1}{3}} ? {(27)}^{\frac{1}{3}}$

$? {(26)}^{\frac{1}{3}} = 3 + 4 y = 3 + \frac{d y}{d x} A x = 3 + \frac{1}{3 x^{\frac{2}{3}}} A x,$

$= 3 ? \frac{1}{3 {(2 F)}^{\frac{2}{3}}}$

$= 3 ? \frac{1}{27}$

$= \frac{81 ? 1}{27} = \frac{80}{27} = 2.962 .$

(viii) ${(255)}^{\frac{1}{4}}$

A.(viii)

Let $y = x^{\frac{1}{4}} .$ Let x = 256 and ?x = 1.

Then, $? y = {(x + ? x)}^{\frac{1}{4}} ? x^{\frac{1}{4}} .$

$= {(255)}^{\frac{1}{4}} ? {(256)}^{\frac{1}{4}}$

$? {(255)}^{\frac{1}{4}} = {(256)}^{\frac{1}{4}} + 4 y = 4 + \frac{d y}{d x} A x .$

$= 4 + \frac{1}{4 x^{\frac{3}{4}}} ? 4 x$

$= 4 \frac{? 1}{4 {(256)}^{\frac{3}{4}}}$

$= 4 ? \frac{1}{256}$

$= \frac{1024 ? 1}{256}$

$= \frac{1023}{256} = 3.996$

(ix) ${(82)}^{\frac{1}{4}}$

A.(ix)

...more

(i) Let y= ?x : Let x = 25 and x = 0. 3.

Then, ?y = ?x+?x $?x$

$=?25.3 ?25$

$=?25.3 ? 5$

$?25.3 = 5 + ? y ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? y ~ d y .$

= 5 + dy

= $5 + (\frac{d y}{d x}) A x .$

$= 5 + \frac{1}{2?x} ? x .$

$= 5 + \frac{1}{2?25} ? 0.3$

$= 5 + \frac{0.3}{2 * 5}$

= 5 + 0.03

$?25.3 = 5.030$

(ii) ?49.5

A.(ii)

Let y = ?x $.$ Let x = 49 and x = 0.5.

Then, $? y =?x+?x ?x .$

$=?49.5 ?49$

$?49.5 = 7 + ? y = 7 + {(\frac{d y}{d x})}_{}^{? x}$

$= 7 + \frac{1}{2?x} ? x$

$= 7 + \frac{1}{2?49} * (0.5)$

$= 7 + \frac{0.5}{14}$

= 7 + 0.0357.

$?49.5 = 7 ? 035$

(iii) ?0.6

A.(iii)

Let y = ?x $.$ Let x = 0.64 and ?x = 0.04.

Then, $? y =?x+Ax ?x$

$=?0.64-0.04 ?0.64 .$

$=?0.6 ? 0.8$

$?0.6= 0.8 + ? y = 0.8 + (\frac{d y}{d x}) ? x$

$= 0.8 + \frac{1}{2?x} ? x$

$= 0.8 + \frac{1}{2?0.64} * (? ? 0.04)$

$= 0.8 \frac{? 0.04}{2 * 0.8}$

= 0.8 - 0.025.

= 0.775.

(iv) ${(0.009)}^{\frac{1}{3}}$

A.(iv)

Let $y = x^{\frac{1}{3}}$ Let x = 0.008 and ?x = 0.00 1.

Then, ?y = ${[x + ? x]}^{\frac{1}{3}} ? {[x]}^{\frac{1}{3}}$

$= {(0.009)}^{\frac{1}{3}} ? {(0.008)}^{\frac{1}{3}}$

${(0.009)}^{\frac{1}{3}} = 0.2 + ? y = 0.2 + \frac{d y}{d x} ? ? x$

$= 0.2 + \frac{1}{3 {(x^{\frac{1}{3}})}^{2}} ? x$

$= 0.2 + \frac{1}{3 {[{(0.008)}^{\frac{1}{3}}]}^{2}} * (0.001)$

$= 0.2 + \frac{0.001}{3 * {(0.0)}^{2}} = 0.2 + \frac{0.001}{0.12}$

= 0.2 + 0.0083.

= 0.208.

(v) ${(0.999)}^{\frac{1}{10}}$

A.(v)

Let $y = x^{\frac{1}{10}} .$ Let x = 1 and ?x = -0.001

Then, $? y = {(x + ? x)}^{\frac{1}{10}} ? x^{\frac{1}{10}}$

$= {(0.999)}^{\frac{1}{10}} ? {(1)}^{\frac{1}{10}}$

$? 1 {(0.999)}^{\frac{1}{10}} = 1 + A y$

$= 1 + \frac{d y}{d x} ? x .$

$= 1 + \frac{1}{10 x^{\frac{9}{10}}} * ? x$

$= 1 ? \frac{0.001}{10 (. 1^{\frac{9}{10}})} = 1 ? \frac{0.001}{10} = 1 ? 0.0001$

= 0.999.

(vi) ${(15)}^{\frac{1}{4}}$

A.(vi)

Let $y = x^{\frac{1}{4}} .$ Then, x = 16 and ?x = 1.

Then, $? y = {(x + A x)}^{\frac{1}{4}} ? x^{\frac{1}{4}} .$

$= {(15)}^{\frac{1}{4}} ? {(16)}^{\frac{1}{4}}$

$? {(15)}^{\frac{1}{4}} = 2 + A y = 2 + \frac{d y}{d x} A x$

$= 2 + \frac{1}{4 x^{\frac{3}{4}}} ? (? 1)$

$= 4 ? \frac{1}{4 {(16)}^{\frac{3}{4}}}$

$= 2 ? \frac{1}{4 * 8}$

$= 4 ? \frac{1}{32}$

$= \frac{64 ? 1}{32} = \frac{63}{32} = 1.968$

(vii) ${(26)}^{\frac{1}{3}}$

A.(vii)

Let $y = x^{\frac{1}{3}} .$ Let x = 27 and ?x = 1.

Then, $? y = {(x + ? x)}^{\frac{1}{3}} ? x^{\frac{1}{3}}$

$= {(26)}^{\frac{1}{3}} ? {(27)}^{\frac{1}{3}}$

$? {(26)}^{\frac{1}{3}} = 3 + 4 y = 3 + \frac{d y}{d x} A x = 3 + \frac{1}{3 x^{\frac{2}{3}}} A x,$

$= 3 ? \frac{1}{3 {(2 F)}^{\frac{2}{3}}}$

$= 3 ? \frac{1}{27}$

$= \frac{81 ? 1}{27} = \frac{80}{27} = 2.962 .$

(viii) ${(255)}^{\frac{1}{4}}$

A.(viii)

Let $y = x^{\frac{1}{4}} .$ Let x = 256 and ?x = 1.

Then, $? y = {(x + ? x)}^{\frac{1}{4}} ? x^{\frac{1}{4}} .$

$= {(255)}^{\frac{1}{4}} ? {(256)}^{\frac{1}{4}}$

$? {(255)}^{\frac{1}{4}} = {(256)}^{\frac{1}{4}} + 4 y = 4 + \frac{d y}{d x} A x .$

$= 4 + \frac{1}{4 x^{\frac{3}{4}}} ? 4 x$

$= 4 \frac{? 1}{4 {(256)}^{\frac{3}{4}}}$

$= 4 ? \frac{1}{256}$

$= \frac{1024 ? 1}{256}$

$= \frac{1023}{256} = 3.996$

(ix) ${(82)}^{\frac{1}{4}}$

A.(ix)

Let $y = x^{\frac{1}{4}} .$ let x = 81 and ?x = 1.

Then, $? y = {(x + 4 x)}^{\frac{1}{4}} ? x^{\frac{1}{4}}$

$= {(82)}^{\frac{1}{4}} ? {(81)}^{\frac{1}{4}}$

$7 {(82)}^{\frac{1}{4}} = 3 + 4 y = 3 + \frac{d y}{d x} ? x$

$= 3 + \frac{1}{4 x^{\frac{3}{4}}} ? ? x$

$= 3 + \frac{1}{4 {(81)}^{\frac{3}{4}}}$

$= 3 + \frac{1}{4 * 3^{3}}$

$= 3 + \frac{1}{108} = \frac{324 + 1}{108} = \frac{325}{108} = 3.001 .$

(x) ${(401)}^{\frac{1}{2}}$

A.(x)

Let y = $x^{\frac{1}{2}}$ = ?x $.$ Let x = 400 and ?x = 1.

Then, $? y = {(x + ? x)}^{\frac{1}{2}} ? x^{\frac{1}{2}} .$

$? ? ? y = {(401)}^{\frac{1}{2}} ? {(400)}^{\frac{1}{2}}$

$? ? {(401)}^{\frac{1}{2}} = 20 ? + ? y = 20 + \frac{d y}{d x} ? x$

$= 20 + \frac{1}{2?x} ? x$

$= 20 + \frac{1}{2?400}$

$= 20 + \frac{1}{2 * 20}$

$= 20 + \frac{1}{40}$

$= \frac{800 + 1}{40} = \frac{801}{40} = 20.025 .$

(xi) ${(0.0037)}^{\frac{1}{2}}$

A.(xi)

Let $y = x^{\frac{1}{2}}$ Let x = 0.0036 and ?x = 0.0001

Then, $? y =?x+?x ?x$

$=?0.0037 ?0.0036$

$?0.0037 = 0.06 + D y = 0.06 + \frac{d y}{d x} ? x = 0.06 + \frac{x}{2?x}$

$= 0.06 + \frac{0.001}{2?0.0036}$

$= 0.06 + \frac{0.001}{2 * 0.06}$

$= 0.06 + \frac{0.001}{0.12 .}$

= 0.06 + 0.0008.

= 0.0608.

(xii) ${(26.57)}^{\frac{1}{3}}$

A.(xii)

Let $y = x^{\frac{1}{3}} .$ Let x = 27 and ?x = 0.43.

Then, $? y = {(x + A x)}^{\frac{1}{3}} ? {(x)}^{\frac{1}{3}}$

$= {(26.57)}^{\frac{1}{3}} ? {(27)}^{\frac{1}{3}}$

$? {(26.57)}^{\frac{1}{3}} = 3 + 4 y = 3 + \frac{d y}{d x} ? x = 3 + \frac{1}{3 x^{\frac{2}{3}}} ? ? x .$

$= 3 + \frac{1}{3 {(27)}^{\frac{2}{3}}} ? less00New answer posted 7 months ago Class 12th Application of Derivatives 64. The line y = x + 1 is a tangent to the curve y 2 = 4x at the point (A) (1, 2) (B) (2, 1) (C) (1, - 2) (D) (- 1, 2) 0 Follower 2 Views Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 The given eqn of curve is y^{2} = 4 x . Then, differentiating wrt x we get, 2 y \frac{d y}{d x} = 4 \Rightarrow \frac{d y}{d x} = \frac{2}{y} which is the slope of the tangent to the curve. The line y = x + 1 compared to y = m x + c gives slope of line = 1. Since, tangent is the line we have, \frac{2}{y} = 1 . \Rightarrow y = 2 Putting y = 2 in y^{2} = 4 x we get, 4 x = 2^{2} \Rightarrow x = 1 . Hence, the required point is (1, 2) Option (A) is correct. 00New answer posted 7 months ago Class 12th Application of Derivatives 63. The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is (A) 3 (B) \frac{1}{3} (C) -3 (D) - \frac{1}{3} 0 Follower 2 Views Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 Given, y = 2 x^{2} + 3 s i n x Slope of tangent, \frac{d y}{d x} = 4 x + 3 c o s x {\frac{d y}{d x} |}_{x = 0} = 4 * 0 + 3 * c o s 0 = 3 So, slope of normal = \frac{- 1}{3} Option (D) is correct. 00New answer posted 7 months ago Class 12th Application of Derivatives 62. Find the equation of the tangent to the curve y = \sqrt3x - 2 which is parallel to the line 4x - 2y + 5 = 0. 0 Follower 1 View Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 Kindly go through the solution 00New answer posted 7 months ago Class 12th Application of Derivatives 61. Find the equations of the tangent and normal to the hyperbola \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 at the point (x_{0}, y_{0}) 0 Follower 2 Views Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 The given eq n of the hyperbola is \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1______(1) Differentiating eqn (1) wrt 'x' we get, \frac{2 x}{a^{2}} - \frac{2 y}{b^{2}} \frac{d y}{d x} = 0 \Rightarrow \frac{2 y}{b^{2}} \frac{d y}{d x} = \frac{2 x}{a^{2}} \Rightarrow \frac{d y}{d x} = \frac{b^{2} x}{a^{2} y} {\frac{d y}{d x} |}_{(x, y)} = (x_{0}, y_{0}) \frac{b^{2} x_{0}}{a^{2} y_{0}} is the reqd slope of tangent to the curve So, eq n of tangent at point (x_{0}, y_{0}) is y - y_{0} = \frac{b^{2} x_{0}}{a^{2} y_{0}} (x - x_{0}) . \Rightarrow \frac{y y_{0}}{b^{2}} - \frac{{y_{0}}^{2}}{b^{2}} = \frac{x x_{0}}{a^{2}} - \frac{{x_{0}}^{2}}{a^{2}} \Rightarrow \frac{x x_{0}}{a^{2}} - \frac{y y_{0}}{b^{2}} = \frac{{x_{0}}^{2}}{a^{2}} - \frac{{y_{0}}^{2}}{b^{2}} As (x_{0}, y_{0}) lies on the parabola given by eqn (1) we write, \frac{{x_{0}}^{2}}{a^{2}} - \frac{{y_{0}}^{2}}{b^{2}} = 1 Hence, \frac{x x_{0}}{a^{2}} - \frac{y y_{0}}{b^{2}} = 1 00New answer posted 7 months ago Class 12th Application of Derivatives 60. Prove that the curves x = y 2 and xy = k cut at right angles* if 8k 2 = 1. 0 Follower 2 Views Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 The given eq n of the curves are x = y^{2}________(1) and x y = x___________(2) Differentiating eqn (1) and (2) wrt 'x' we get, \frac{d y^{2}}{d x} = \frac{d x}{d x} \to 2 y \frac{d y}{d x} = 1 \to \frac{d y}{d x} = \frac{1}{2 y}_________(3) and \frac{d}{d x} (x y) = \frac{d}{d x} (x) \to x \frac{d y}{d x} + y = 0 \to \frac{d y}{d x} = - \frac{y}{x}_________(4) Since the two curves cut each other at right angles we get, (\frac{1}{2 y}) * (\frac{- y}{x}) = - 1 . \to 2 x = 1________(5) The point of intersection can be solve from eqn (1) and (2), y^{2} . y = k \to y^{3} = k \to y = k^{1 / 3} ∴ x = y^{2} = r^{2 / 3} . Hence, using eq n (5) we get, 2 {(r)}^{2 / 3} = 1 . \Rightarrow {[2 r^{2 / 3}]}^{3} = 1^{3} \Rightarrow 8 r^{2} = 1 Hence proved 00New answer posted 7 months ago Class 12th Application of Derivatives 59. Find the equations of the tangent and normal to the parabola y 2 = 4ax at the point (at 2, 2at). 0 Follower 2 Views Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 The given of the parabola is y^{2} = 4 a x slope of tangent is given by \frac{d}{d x} y^{2} = \frac{d}{d x} 4 a x \to 2 y \frac{d y}{d x} = 4 a \Rightarrow \frac{d y}{d x} = \frac{2 a}{y} . {\frac{d y}{d x} |}_{(a t^{2}, 2 a t)} = \frac{2 a}{2 a t} = \frac{1}{t} so, slope of normal so, slope of normal = \frac{- 1}{(\frac{1}{t})} = - t Hence eq n of tangent at point (a t^{2}, 2 a t) is y - 2 a t = \frac{1}{t} (x - a t^{2}) \to t y - 2 a t^{2} = x - a t^{2} \to x - t y - a t^{2} + 2 a t^{2} = 0 x - t y + a t^{2} = 0 And eq n of normal at point (a t^{2}, 2 a t) is (y - 2 a t) = (- t) (x - a t^{2}) \to y - 2 a t = - t x + a t^{3} \Rightarrow t x + y - 2 a t + a t^{3} = 0 \Rightarrow t x + y - a t (2 + t^{2}) = 0 00New answer posted 7 months ago Class 12th Application of Derivatives 58. Find the equation of the normals to the curve y = x 3 + 2x + 6 which are parallel to the line x + 14y + 4 = 0. 0 Follower 1 View Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 The given eq n of the curve is y = x^{3} + 2 x + 6_____(1) slope of tangent to the curve, \frac{d y}{d x} = 3 x^{2} + 2 so, slope of normal to the curve = \frac{- 1}{3 x^{2} + 2} Now, the line x + 14 y + 4 = 0 \to y = - \frac{1}{14} x - \frac{4}{14} compared to y = m x + c gives slope of line = - \frac{1}{14} As the normal is parallel to the line \Rightarrow \frac{- 1}{3 x^{2} + 2} = - \frac{1}{14} \to 3 x^{2} + 2 = 14 \Rightarrow 3 x^{2} = 12 \to x^{2} = 4 \Rightarrow x = \pm 2 When x = 2, y = {(2)}^{3} + 2 (2) + 6 = 8 + 4 + 6 = 18 and when x = - 2, y = {(- 2)}^{3} + 2 (- 2) + 6 = - 8 - 4 + 6 = - 6 The point of contact of the normal are (2, 18) and (-2, -6) Hence the eq n of normal are y - 18 = - \frac{1}{14} (x - 2) and y - (- 6) = \frac{- 1}{14} [x - (- 2)] \Rightarrow 14 y - 252 = - x + 2 \Rightarrow y + 6 = \frac{- 1}{14} (x + 2) \Rightarrow x + 14 y - 254 = 0 \Rightarrow 14 y + 84 = - x - 2 \Rightarrow x + 14 y + 86 = 0 . 00New answer posted 7 months ago Class 12th Application of Derivatives 57. Find the equation of the normal at the point (am 2,am 3) for the curve ay 2 = x 3 0 Follower 5 Views Follow Characters 0 /2500 Disclaimer: Please note that external links or URLs are not allowed. Non adherence will lead to removal of the comment Cancel Post V Vishal Baghel Contributor-Level 10 The given eq n of curve is a y^{2} = x^{3}_____(1) Differentiating eq n (1) wrt.x we get, 2 a y \frac{d y}{d x} = 3 x^{2} . \Rightarrow \frac{d y}{d x} = \frac{3 x^{2}}{2 a y}, slope of tangent {\frac{d y}{d x} |}_{(x, y) = (a m^{2}, a m^{3})} = \frac{3 {[a m^{2}]}^{2}}{2 a [a m^{3}]} = \frac{3 a^{2} m^{4}}{2 a^{2} m^{3}} = \frac{3 m}{2} corresponding slope of normal = \frac{- 1}{(3 m / 2)} = - \frac{2}{3 m} Hence, eq n of normal at (a m^{2}, a m^{3}) is y - a m^{3} = - \frac{2}{3 m} (x - a m^{2}) . \Rightarrow 3 m y - 3 a m^{4} = - 2 x + 2 a m^{2} \Rightarrow 2 x + 3 m y - 3 a m^{4} - 2 a m^{2} = 0 \Rightarrow 2 x + 3 m y - a m^{2} (2 + 3 m^{2}) = 0 00❮ 958959960961962963964965966 ❯Taking an Exam? Selecting a College? Get authentic answers from experts, students and alumni that you won't find anywhere else Sign Up on Shiksha On Shiksha, get access to 66k Colleges 1.2k Exams 684k Reviews 1800k Answers .write-a-review-widget h2.tbSec2 {
border-bottom: none;
padding: 0 0 16px;
margin: 0px;
font-size: 16px;
line-height: 1.5;
font-weight: 600;
}
.write-a-review-widget .link-btn {
text-align: center;
}
.static-widget{
margin-bottom: 16px;
box-shadow: 0 2px 2px 0 rgb(0 0 0 / 16%), 0 0 0 1px rgb(0 0 0 / 8%);
background: #fff;
padding: 12px 12px 16px;
}
.button {
display: inline-block;
cursor: pointer;
font-weight: 600;
text-align: center;
vertical-align: middle;
-webkit-user-select: none;
-moz-user-select: none;
-ms-user-select: none;
user-select: none;
background-color: transparent;
border: 1px solid transparent;
padding: 0 10px;
font-size: .875rem;
height: 34px;
line-height: 32px;
border-radius: 2px;
outline: 0;
white-space: nowrap;
min-width: 90px;
text-transform: capitalize;
}
a.button--orange {
background-color: #f37921;
border-color: #f37921;
color: #fff;
} Share Your College Life Experience Write a Review Community Guidelines User Points System Questions Discussions Tagsvar GA_currentPage = "TAG DETAIL PAGE";
var ga_user_level = "Non-Logged In";
function LazyLoadAnADesktopCallback(){
$LAB
.script('//js.shiksha.ws/public/js/build/ajax-api.1e2339.js',
'//js.shiksha.ws/public/js/build/ana_desktop.57940d.js',
'//js.shiksha.ws/public/js/build/quesDiscPosting.8361d6.js',
'//js.shiksha.ws/public/js/build/jquery.tinyscrollbar.min.v5.dc5c57.js',
'//js.shiksha.ws/public/js/build/bottomStickyRegistrationLayer.c9e9a3.js')
.wait(function(){
LazyLoadCallBackTDP();
prepareClickDataTDP();
});
}var getcHostName = "https://www.shiksha.com/resources/college-comparison";1234 Compare Remove All CompareCollege Comparison Cancel Ok.ana-posting-overlay{position: fixed;left: 0;right: 0;top: 0;bottom: 0;background: rgba(0,0,0,.4);z-index: 10000;}
.ana-posting-iframe-bx{z-index: 10000;width: 1022px;height: 630px;max-height:100%;max-width:100%;position: fixed;margin: 0 auto;box-sizing: border-box;top: 50%;left: 50%;transform: translate(-50%,-50%);overflow: hidden;border-radius: 8px;}
a#closeAnAPopup {background: #fff;border-radius: 1000px;height: 30px;width: 30px;text-align: center;font-size: 12px;right: -12px;top: -12px;box-shadow: 0px 2px 4px 0px rgba(0,0,0,0.8);}
.ana-posting-close{top: -3px;right: 3px;font-size: 20px !important;color: #666 !important;cursor: pointer;margin: 0 auto;position: absolute;}
.ana-posting-iframe{border: none;height: 100%;width: 100%;}
.hide{display: none;}
body.freeze{position: fixed;width:100%;overflow:hidden}
@media screen and (max-width:767px) {
.ana-posting-iframe-bx{width: 100%; height: 100%;}
.ana-posting-overlay{background:#fff}
}\timesvar ANA_POSTING_PAGE2 = 'aHR0cHM6Ly93d3cuc2hpa3NoYS5jb20vdWdjL2FuYS1jb250ZW50LXBvc3Rpbmc=';// Attach window click event handler for GA tracking
if(typeof loadNewHomePageWidget == 'function'){
loadNewHomePageWidget('/shiksha/loadAjaxForm/abroadtab','hmpgrdsn_tababroad');
}\times if(typeof(googletag) != 'undefined'){ googletag.cmd.push(function() { googletag.display("div-gpt-ad-1547104965023-0"); }); }This website uses Cookies and related technologies for the site to function correctly and securely, improve & personalise your browsing experience, analyse traffic, and support our marketing efforts and serve the Core Purpose. By continuing to browse the site, you agree to Privacy Policy and Cookie Policy . OKGet our experts to answer your questions within 24 Hrs Ask Question Shiksha About Us Management Team Careers Shiksha Authors Colleges Client login Advertise with us Add Colleges Contact Us Others FAQs Grievances Notices / Summons Privacy Sitemap Terms & Conditions Our Group Infoedge.in Naukri.com Naukri Campus Naukrigulf 99acres.com Jeevansathi.com AmbitionBox.com Naukri Learning Job Hai MBA : MBA Home Top MBA Colleges MBA Colleges Executive MBA Colleges MBA Exams Engineering : Engineering Top Engineering Colleges Engineering Colleges Engineering Exams JEE Main JEE Advanced Medicine : NEET NEET PG AIIMS PG JIPMER PG PGIMER Exam Top Medical Colleges Medical Colleges Medical Exams Other Courses : Animation B Com B Sc BBA CA Fashion & Textile Design Hotel Management Law Mass Communication MBBS MCA M.Tech BCA Pharmacy M Sc Study Abroad : Study Abroad Home BTech abroad MBA abroad MS abroad GRE GMAT SAT IELTS TOEFL Sarkari Exams : SSC CGL IBPS PO SBI PO NDA UPSC Civil Services Exam IES SSC CHSL AFCAT IBPS CWE RRB SSC JE CDS SBI Clerk IBPS Clerk Resources : Careers after 12th Courses After 12th Education Boards Ask a Question Discussions Write a college review Articles Shiksha Ask & Answer App Education Trends Important Updates : JEE Main 2026 Jan Question Paper with Answer Key CMAT Result 2026 CMAT Cutoff CMAT Score vs Percentile 2026 XAT Cut off 2026 NEET 2026 CAT 2026 JEE Main 2026 Admit Card JEE Main 2026 JEE Main Rank Predictor JEE Main 2026 College Predictor JEE Main 2026 Answer Key JEE Main Expected Cutoff WBJEE 2026 BITSAT 2026 VITEEE 2026 Trade Marks belong to the respective owners. Copyright © 2026 Info edge India Ltd. All rights reserved.try{ overlayViewsArray.push(new Array('common/calendardiv','calendardivId')); }catch(e){ }try{ overlayViewsArray.push(new Array('network/commonOverlay','addRequestOverlay')); }catch(e){ }window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());

gtag('config', 'G-F0XEJFWK9T');// added for switch tracking of search results on and off
var track_search_results_flag = "1";
var facebook_channel_path = "https://www.shiksha.com/public/channel.html";

function proceedToPostQuestionFromHome(objForm,id){
objForm.setAttribute("method",'get');
objForm.setAttribute("action",'https://ask.shiksha.com/messageBoard/MsgBoard/postQuestionFromCafeForm');
objForm.submit();
}try{ jsb9eraseCookie("jsb9Track");
var prevWindowOnunload = window.onbeforeunload; window.onbeforeunload = function(){ try{ if(typeof(prevWindowOnunload) == "function") { prevWindowOnunload.call(); } jsb9onUnloadTracking(); }catch(e){ } }
function jsb9onUnloadTracking() { jsb9eraseCookie("jsb9Track"); var date = new Date(); var presentTime = date.getTime(); var presentUrl = window.location.href; jsb9createCookie("jsb9Track",presentTime+"|"+presentUrl,5); } var date = new Date(); jsb9TrackEndTime = date.getTime(); function jsb9TrackTime() { var jsb9date = new Date(); jsb9TrackFinalLoad=jsb9date.getTime(); if(typeof(jsb9TrackVal) == "string") { var cookieArr = jsb9TrackVal.split('|'); var prevTime = cookieArr[0]; var refererUrl = cookieArr[1]; var jsb9Iframe = document.createElement('div');jsb9Iframe.style.cssText='height:0px;overflow:hidden;'; jsb9Iframe.id = 'jsb9Div'; var style = 'border:0;width:0;height:0;display:none'; var jsb9ServerTime = 475.99291801453; var presentUrl = window.location.href; var customTrack = ""; for(var i in jsb9recordTimes) { customTrack += "|"+i+":"+jsb9recordTimes[i]; } var data = presentUrl+"|"+refererUrl+"|"+prevTime+"|"+jsb9TrackStartTime+"|"+jsb9TrackEndTime+"|"+jsb9TrackFinalLoad+"|"+jsb9ServerTime+customTrack; jsb9Iframe.innerHTML = '<iframe border="0" height=0 widht=0 style="visibility: hidden" src="https://track.99acres.com/images/zero.gif?data='+data+'"></iframe>';
document.body.appendChild(jsb9Iframe); } } }catch(e){ }var shikshaProduct = 'anaDesktopV2';/**
* Method loads all required scripts for Unified Registration
* callback function is loadRequiredDataForUnifiedRegistrationProcess
* callback API will be alwys called either file is already loaded or not
*/
function initForUnifiedRegistration()
{
LazyLoad.loadOnce([
'//js.shiksha.ws/public/js/build/ajax-api.1e2339.js'
],loadRequiredDataForUnifiedRegistrationProcess,null,null,true);
}

/*
Function which put values into global vars. like is_ldb user or cross btn click
*/

function loadRequiredDataForUnifiedRegistrationProcess()
{
/* ajax to set if user register or not START */
//checkLdbUser();
/* ajax to set if user register or not END */
/* set variable to check whether user has clicked unified overlay or not*/
unified_form_overlay1_cancel_clicked = getCookie('is_unified_overlay1_clicked');
unified_form_overlay2_cancel_clicked = getCookie('is_unified_overlay2_clicked');
unified_form_overlay3_cancel_clicked = getCookie('is_unified_overlay3_clicked');
/* set Form submit url for diff types of overlays */
if(typeof(arr_unified) !== 'undefined') {
ShikshaUnifiedRegistarion.url_unified = ShikshaUnifiedRegistarion.ajaxUrlHelper(arr_unified);
}
if($('homepagePromotionCarousel')) {
//if($('questionText')) { $('questionText').value = 'Make an informed career choice, ask the expert now!';}
}
// showResetPasswordLayer();
}
/* UNIFIED REGISTRATION APIs END */$j = $.noConflict();var lazyLoadJsFiles = []
function lazyLoadJsFilesInParallel() {
if(lazyLoadJsFiles.length > 0) {
LazyLoad.loadOnce(lazyLoadJsFiles,function(){},null,null,true);
}
}

function LazyLoadAnAContactUsCallback(){
$LAB.script('//js.shiksha.ws/public/js/build/quesDiscPosting.8361d6.js').wait(function(){
LazyLoadAnAContactUs();
});
}

function loadJsFilesInParallel(){
$j(document).trigger('labLoadedJs');
$LAB
.script("//js.shiksha.ws/public/js/build/AutoSuggestor.512dd5.js")
.wait(function(){
if(SHOW_AUTOSUGGESTOR_JS){
autosuggestorInstanceCheck = setInterval(function(){
var fileLoaded = false;
try{
var aso = new AutoSuggestor();
fileLoaded = true;
} catch(e) {
fileLoaded = false;
}
if(fileLoaded){
clearInterval(autosuggestorInstanceCheck);
if(typeof(initializeAutoSuggestorInstance) == 'function') {
initializeAutoSuggestorInstance();
}
if(typeof(initializeAutoSuggestorInstanceSearchV2) == 'function') {
try {
initializeAutoSuggestorInstanceSearchV2('{"suggestionContainerClass":"search-college-layer","bucketCount":4,"searchVersion":"2","tabPressedHandler":"handleAutoSuggestorTabPressed","enterPressedHandler":"handleAutoSuggestorEnterPressedSearch","mouseClickedHandler":"handleAutoSuggestorMouseClickedSearch","navigationKeysHandler":"handleNavigationKeysHandler","objectName":"autoSuggestorInstanceSearch","searchBoxId":"searchby-college","suggestionContainerId":"search-college-layer","typeAhead":0,"suggestionType":"course_and_institute","suggestionCount":8,"autoSuggestorUrl":"\/search\/AutoSuggestorV2\/getSuggestionsFromSolr\/","isMobileSearch":false,"showGrouping":1,"getTrendingSuggestions":1}');
initializeAutoSuggestorInstanceSearchV2('{"suggestionContainerClass":"search-college-layer","bucketCount":4,"searchVersion":"2","tabPressedHandler":"handleAutoSuggestorTabPressedCareers","enterPressedHandler":"handleAutoSuggestorEnterPressedCareers","mouseClickedHandler":"handleAutoSuggestorEnterPressedCareers","objectName":"autoSuggestorInstanceCareer","searchBoxId":"searchby-career","suggestionContainerId":"search-career-layer","getTrendingSuggestions":1,"typeAhead":0,"disableCache":1,"suggestionType":"career","suggestionCount":8}');
initializeAutoSuggestorInstanceSearchV2('{"suggestionContainerClass":"search-college-layer","bucketCount":4,"searchVersion":"2","tabPressedHandler":"handleAutoSuggestorTabPressedQuestion","enterPressedHandler":"handleAutoSuggestorEnterPressedQuestion","mouseClickedHandler":"handleAutoSuggestorEnterPressedQuestion","mouseClickedHandlerLastElement":"handleAutoSuggestorEnterPressedAskQuestion","askNewQuestionURL":"https:\/\/ask.shiksha.com","mouseClickedHandlerCTA":"handleAutoSuggestorEnterPressedCTA","backKeyHandler":"handleAutoSuggestorBackKeyPressedQuestion","objectName":"autoSuggestorInstanceQuestion","searchBoxId":"searchby-question","suggestionContainerId":"search-question-layer","removeExactMatch":1,"suggestionType":"question","suggestionCount":8,"isMobileSearch":false,"autoSuggestorUrl":"\/search\/AutoSuggestorV2\/getSuggestionsFromSolr\/","showGrouping":1,"getTrendingSuggestions":1}');
initializeAutoSuggestorInstanceSearchV2('{"suggestionContainerClass":"search-college-layer","bucketCount":4,"searchVersion":"2","tabPressedHandler":"handleAutoSuggestorTabPressedExams","enterPressedHandler":"handleAutoSuggestorEnterPressedExams","mouseClickedHandler":"handleAutoSuggestorEnterPressedExams","backKeyHandler":"handleAutoSuggestorBackKeyPressedExams","objectName":"autoSuggestorInstanceExam","searchBoxId":"searchby-exam","suggestionContainerId":"search-exam-layer","suggestionType":"exam","suggestionCount":8,"autoSuggestorUrl":"\/search\/AutoSuggestorV2\/getSuggestionsFromSolr\/","showGrouping":1,"getTrendingSuggestions":1}');
tagsASConfig = '{"suggestionContainerClass":"search-college-layer","bucketCount":4,"searchVersion":"2","enterPressedHandler":"handleAutoSuggestorEnterPressedTags","mouseClickedHandler":"handleAutoSuggestorEnterPressedTags","objectName":"autoSuggestorInstanceForTags","searchBoxId":"tagSearch","suggestionContainerId":"tagSearch_container","typeAhead":0,"suggestionType":"tag","suggestionCount":10,"autoSuggestorUrl":"\/Tagging\/TaggingDesktop\/getAutoSuggestor","showGrouping":1,"disableCache":1,"removePartialMatch":0}';
initializeAutoSuggestorInstanceSearchV2(tagsASConfig);
initializeAutoSuggestorInstanceSearchV2('{"suggestionContainerClass":"search-college-layer","searchVersion":"2","enterPressedHandler":"handleAutoSuggestorEnterPressedTags","mouseClickedHandler":"handleAutoSuggestorEnterPressedTags","objectName":"autoSuggestorInstanceForTagsQDP","searchBoxId":"tagSearchQDP","suggestionContainerId":"tagSearchQDP_container","typeAhead":0,"suggestionType":"tag","suggestionCount":6,"autoSuggestorUrl":"\/Tagging\/TaggingDesktop\/getAutoSuggestor","showGrouping":1,"disableCache":1,"callBackFunctionAfterBuildingSuggestionContainer":"showSuggestedTags","callBackFunctionOnInputKeysPressed":"showSuggestedTags"}');
}
catch(e) {
console.log(e);
}
}
if(typeof(initializeAutoSuggestorInstancesForCollgeReviews) == 'function') {
initializeAutoSuggestorInstancesForCollgeReviews();
}
if(typeof(initializeAutoSuggestorInstancesForCampusConnect) == 'function') {
initializeAutoSuggestorInstancesForCampusConnect();
}

if(typeof(initializeAutoSuggestorInstanceAlt) == 'function') {
initializeAutoSuggestorInstanceAlt();
}
}
},1000);
}
});
LazyLoadAnADesktopCallback();
}
(function(g,b,d){var c=b.head||b.getElementsByTagName("head"),D="readyState",E="onreadystatechange",F="DOMContentLoaded",G="addEventListener",H=setTimeout;
function f(){ loadJsFilesInParallel(); /*if(typeof CTACallBackSearch == 'function') CTACallBackSearch();*/} H(function(){if("item"in c){if(!c[0]){H(arguments.callee,25);return}c=c[0]}var a=b.createElement("script"),e=false;a.onload=a[E]=function(){if((a[D]&&a[D]!=="complete"&&a[D]!=="loaded")||e){return false}a.onload=a[E]=null;e=true;f()};
a.src="//js.shiksha.ws/public/js/LAB.min.js";c.insertBefore(a,c.firstChild)},0);if(b[D]==null&&b[G]){b[D]="loading";b[G](F,d=function(){b.removeEventListener(F,d,false);b[D]="complete"},false)}})(this,document);lazyLoadCss('//css.shiksha.ws/public/css/build/socialSharingInner.min.5de709.css');var reset_password_token = '';
var reset_usremail = '';
var reset_password = '';
var usergroup = '';

//var registration_context = '';
var user_logged_in_pref_data = "";
var userInfo = null;
var firstTimePageLoad = true;var serviceWorker = "service-worker.js";
if ('serviceWorker' in navigator && typeof serviceWorker == 'string' && serviceWorker.length > 0 && typeof registerServiceWorker == 'function') {
registerServiceWorker(serviceWorker);
}
/* function to bind autosuggestor */
if(typeof(bindAutoSuggestorEvents) == 'function'){
bindAutoSuggestorEvents();
}
/* responsible for showing GNB sub-menu on mouse hover */
if(typeof(activateGnbMouseOver) == 'function'){
activateGnbMouseOver();
}
var homepageMiddlePanel, instituteDetailPageClass, cookieDomain = '.shiksha.com';
$j(document).ready(function(){
shikshaOnreadyEventPC();
getSocialSharingLayer();
});
$j(window).on('load',function(){
shikshaOnloadEventPC();
if(typeof isUserLoggedIn !='undefined' && isUserLoggedIn && typeof getPredictorList != 'undefined' && typeof getPredictorList == 'function'){
getPredictorList();
}
});window.pushNotiConf = {
deviceType : 'desktop'
};
if(document.getElementById("pushNotificationContainer") != null){
var d = new Date();
var dStr = d.getDate()+''+d.getMonth()+''+d.getFullYear()+'v10';
var randomId = Math.floor(Math.random() * 100);

var loadNotificationSDK = function() {
var obj = document.createElement('script');
/* obj.src = 'https://localshiksha.com/public/js/shikshaPushNotification.js?'+dStr+randomId;*/
obj.src = '//js.shiksha.ws/public/js/build/shikshaPushNotification.b0fa7c.js?'+dStr+randomId;
obj.async = true;
document.head.appendChild(obj);
};

var helperObj = document.createElement('script');
/* helperObj.src = 'https://localshiksha.com/pwa/public/js/push-notification-helpers.js?'+dStr;*/
helperObj.src = '//js.shiksha.ws/pwa/public/push-notification-helpers.js?'+dStr+randomId;
helperObj.async = true;
document.head.appendChild(helperObj);

if (typeof helperObj.onload == 'object') {
helperObj.onload = function(e) {
console.log('notification helper sdk loaded');
loadNotificationSDK();
};
} else {
loadNotificationSDK();
}
if(typeof gaTrackEventCustom == 'function'){
window.phpGATrack = gaTrackEventCustom;
}
}setTimeout(function(){if(typeof loadViewsOnPageLoad == 'function'){loadViewsOnPageLoad();} },2000);var multiLocationCourses = [0];if(shikshaProduct=='CMSExam'){
var elem = document.getElementById("cookieAdSlot-d");
elem.parentNode.removeChild(elem);
}facebook Twitter Google +if (document.addEventListener){
document.addEventListener('mouseup', handleShareLayerHide, false);
} else if (document.attachEvent){
document.attachEvent('onmouseup', handleShareLayerHide);
}

function handleShareLayerHide(e)
{
var target = (e && e.target) || (event && event.srcElement);
var obj = $('socialLayer');
if(target!=obj){
obj.style.display='none';
}
}\times//Load website tour
$j(document).ready(function(){
window.contentMapping = {"Filters":"Filter rankings by publisher, exams, location, specialization etc.","DEB":"Download details of eligibility, admissions, fees, infra etc.","Shortlist":"Save your shortlist, get updates, college recommendations etc.","Compare":"Compare colleges on ranking, placements, reviews, fees etc.","Reviews":"Get honest reviews from students who studied in this college","Questions":"Get answers from the students currently studying in this college","Institute":"View college details, courses offered & recommendations","Course":"View course details, admission process & insights","Exam":"View Exam Detail","QuestionSearch":"Now you can also search from 5 lakh+ answered questions","DownloadGuide":"Get all details offline, receive important updates & more.","QuestionPapers":"Get prep tips & previous years question papers."};
initializeWebsiteTour('cta','anaDesktopV2',contentMapping);
});
lazyLoadCss('//css.shiksha.ws/public/css/build/quesDiscPosting.min.99ce37.css');$

Need guidance on career and education? Ask our experts

Your Question

Class 12th

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience