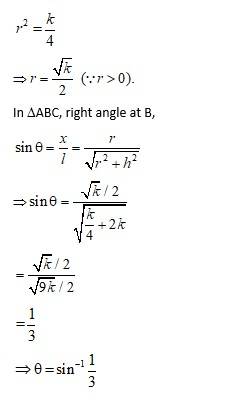Class 12th

Discuss biological and industrial importance of osmosis.

0 Follower 5 Views

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

The process of osmosis is of immense biological and industrial importance as is evident from the following examples:

A. Biological Importance :

(i) Osmosis is responsible for some of the water movement from the soil into the plant roots and then into the top parts of the plant.

(ii) Adding salt to meat to protect it against bacterial action (ie. salting).

(iii) Sugar is used to protect fruits from bacterial attack. Bacterium in canned fruit shrivels and dies as a result of the osmosis process.

(iv) Salt blood cells break due to osmosis when placed in water containing les

...more

0 0

New answer posted

7 months ago

99. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is $s i n^{- 1} \frac{1}{3}$ .

0 Follower 5 Views

Contributor-Level 10

Kindly go through the solution

0 0

New answer posted

7 months ago

When kept in water, raisin swells in size. Name and explain the phenomenon involved with the help of a diagram. Give three applications of the phenomenon.

0 Follower 7 Views

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

Raised increases in size when submerged in water. It's due to a phenomenon known as "Osmosis." The process is depicted graphically in figure. A semipermeable membrane separates a solution from its solvent in this procedure, allowing solvent molecules to pass through but preventing solute particles from passing through.

The passage of solvent molecules from a pure solvent to a solution via a semipermeable membrane is known as osmosis. The following are three osmosis applications:

(i) Osmosis is responsible for some of the water movement from the soil into the plant roots

...more

0 0

New answer posted

7 months ago

Why is it not possible to obtain pure ethanol by fractional distillation? What general name is given to binary mixtures which show deviation from Raoult's law and whose components cannot be separated by fractional distillation. How many types of such mixtures are there?

0 Follower 7 Views

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

"Azeotropes” is the general term for binary mixes that deviate from Rault's law and whose components cannot be separated by fractional distillation. Because of the following reasons, fractional distillation cannot produce pure ethanol: Azeotropes are binary solutions (liquid mixes) with the same composition in the liquid and vapour phases, therefore fractional distillation cannot separate the components of an azeotrope. On fractional distillation, an ethanol-water mixture (obtained via sugar fermentation) yields a solution containing approximately 95 percent ethanol b

...more

0 0

New answer posted

7 months ago

98. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is $t a n^{- 1}$ √2.

0 Follower 5 Views

Contributor-Level 10

Let r, h, l and Ø be the radius, height, slant height and semi-vertical angle respectively of the cone. i.e., r, h, l>0.

Then, Volume V of the cone is

$= \frac{1}{3} π r^{2} h .$

$= \frac{1}{3} π (l^{2} - h^{2}) h$

$= \frac{1}{3} π (l^{2} h - h^{3}) .$

So, $\frac{dV}{d h} = \frac{1}{3} π (l^{2} - 3 h^{2})$

$\frac{d^{2V}}{d h^{2}} = - 2 π h$

0 0

New answer posted

7 months ago

Explain the terms ideal and non-ideal solutions in the light of forces of interactions operating between molecules in liquid solutions.

0 Follower 13 Views

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

Ideal solution: The 'ideal solution' is a binary solution of two volatile liquids that follows Raoult's rule at any concentration and temperature.

Ideal solutions are formed when the intermolecular attractive forces between the solute (A) and the solvent (B) (ie.A-B interaction) are approximately equal to those between the solvent-solvent (A-A) and the solute-solute (BB). Enthalpy of mixing, mixing H=0, in such a perfect solution.

Volume change on mixing, Δ mixing V=0.

Examples: n- hexane and n-heptane.

Non ideal solution: At any concentration and temperature, these

...more

0 0

New answer posted

7 months ago

97. Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 time the radius of the base.

0 Follower 4 Views

Contributor-Level 10

Let r and h be the radius and height of the cone.

The volume V of the cone is.

$= \frac{1}{3} π r^{2} h$

$r^{2} h = \frac{3V}{π} = k (SAY) \Rightarrow r^{2} = \frac{k}{h} .$

And curve surface area S is

0 0

New answer posted

7 months ago

96. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is $\frac{8}{27}$ of the volume of the sphere.

0 Follower 4 Views

Contributor-Level 10

Let r and h be the radius and height of the one in scribed in the sphere of radius R.

Then, is ΔOBC, rt angle at B (h-r)² + r² = R²

$\Rightarrow$ h² + R²- 2hR + h² = R²

$\Rightarrow$ r² = 2hR -h²

Then the volume v of the cone is, $V = \frac{1}{3} * r^{2} h$ $= \frac{1}{3} π (2 h R - h^{2}) h$

$= \frac{1}{3} π (2 {Rh}^{2} - h^{3}) .$

$\Rightarrow \frac{dV}{d h} = \frac{π}{3} (4 Rh - 3 h^{2}) .$

$\frac{d^{2V}}{d h^{2}} = \frac{π}{3} (4R - 6 h) .$

At $\frac{dV}{d h} = 0$

$- \frac{π}{3} (4R h - 3 h^{2}) = 0 .$

4Rh – 3h² = 0.

h(4R – 3h) = 0.

h = 0 and $h = \frac{4 R}{3}$

As h> 0, $h = \frac{4}{3} .$

At $h = \frac{4R}{3}, \frac{d^{2v}}{d h^{2}} = \frac{π}{3} [4 R - 6 * \frac{4rR}{3}]$

$= \frac{1}{3} [4R - 8 R] = - \frac{4 Rπ}{3} < 0$

$h = \frac{4R}{3}$ is a point of maxima.

and $r^{2} = 2 hR - h^{2} = 2 * \frac{4R}{3} R- {(\frac{4R}{3})}^{2}$

$= \frac{3 * 8R^{2}}{9} - \frac{1 6R^{2}}{9}$

$r^{2} = \frac{8R^{2}}{9}$

Hence, Volume of Cone, $= \frac{1}{3} π r^{2} h$

$= \frac{1}{3} π * \frac{8R^{2}}{9} * \frac{4R}{3}$

$= \frac{8}{27} * \frac{4}{3} πR^{3} = \frac{8}{27} *$ Volume of sphere.

0 0

New answer posted

7 months ago

Using Raoult's law explain how the total vapour pressure over the solution is related to mole fraction of components in the following solutions.

(i) CHCl₃ (l) and CH₂Cl₂ (l)

(ii) NaCl(s) and H₂O (l)

0 Follower 9 Views

Contributor-Level 10

This is a long answer type question as classified in NCERT Exemplar

(i) For a binary solution having both components as volatile liquids (viz. CHCl₃ and CH₂Cl₂), the total pressure will be

p= $\frac{t o t a l v a p o u r p r e s s u r e o f t h e g i v e n m i x t u r e}{b i n a r y s o l u t i o n o f t h e g i v e n v o l a t i l e l i q u i d s}$

p₁= partial vapour pressure of component 1 (ie. CHCl₃)

p₂= partial vapour pressure of component 2 (ie. CH₂Cl₂)

(ii) For a solution containing non-volatile solute ie. NaCl (s) and H₂O (l), the Raoult's law is applicable only to vaporisable component (1) ie. H₂O (l) and total vapour pressure is written as

P= P₁= x₁P₁⁰+ x₂P₂⁰

= x₁P₁⁰+ (1-x₁) P₂⁰

(P₁⁰-P₂⁰)X¹ + P₂⁰

p= $\frac{t o t a l v a p o u r p r e s s u r e o f t h e g i v e n m i x t u r e}{b i n a r y s o l u t i o n o f t h e g i v e n v o l a t i l e l i q u i d s}$

p₁= partial vapour pressure of component 1 (CHCl₃ )

0 0

New answer posted

7 months ago

95. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?

0 Follower 2 Views