Tags Physics Gravitation

Physics Gravitation

Get insights from 160 questions on Physics Gravitation, answered by students, alumni, and experts. You may also ask and answer any question you like about Physics Gravitation

Follow Ask Question

160

Questions

Discussions

Active Users

Followers

New answer posted

2 months ago

Physics Gravitation Class 11th

Why is there a negative sign in the total energy formula of a satellite?

0 Follower 3 Views

Aadit Singh Uppal

Contributor-Level 10

The minus sign in the formula indicates that:

A gravitational force exists.
The satellite cannot leave the orbit by itself.
A minimum threshold of energy will be required to move the satellite from its existing orbit.

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

Two planets A and B of equal mass are having their period of revolutions T_A and T_B such that T_A = 2T_B. These planets are revolving in the circular orbits or radii r_A and r_B respectively. Which out of the following would be the correct relationship of their orbits?

0 Follower 2 Views

Raj Pandey

Contributor-Level 9

According to kepler's third law of time period –

${(\frac{T_{A}}{T_{B}})}^{2} = {(\frac{r_{A}}{r_{B}})}^{3} \Rightarrow \frac{r_{A}}{r_{B}} = 4^{1 / 3}$

$\Rightarrow r_{4}^{3} = 4 r_{B}^{3}$

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

The time period of a satellite revolving around earth in a given orbit is 7 hours. If the radius of orbit is increased to three its previous value, then approximate new time period of the satellite will be

0 Follower 3 Views

alok kumar singh

Contributor-Level 10

Kindly go through the solution

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

A planet is revolving around the sun in an elliptical orbit. The mass of planet is m, angular momentum of planet about sun is $L$ , and length of semi major axis is a and eccentricity are $e$ . Time period of revolution of planet is given by

0 Follower 3 Views

alok kumar singh

Contributor-Level 10

$b = a \sqrt[]{1 - e^{2}}$

$\frac{d A}{d t} = \frac{L}{2 m}$

$\frac{A}{T} = \frac{L}{2 m}$

$T = \frac{2 m A}{L} = \frac{2 m π a b}{L} = \frac{2 m π a^{2} \sqrt[]{1 - e^{2}}}{L}$

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

The diagram showing the variation of gravitational potential of earth with distance from the centre of earth is

0 Follower 3 Views

Raj Pandey

Contributor-Level 9

$V_{in} = \frac{- G M}{2 R} [3 - {(\frac{r}{R})}^{2}],$

$V_{s u r f a c e} = \frac{- G M}{R}, V_{out} = \frac{- G M}{r}$

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

Two satellites A and B of masses 200kg and 400kg are revolving round the earth at height of 600km and 1600km respectively. If T_A and T_B are the time periods of A and B respectively then the value of T_B – T_A :

[Given : radius of earth = 6400km, mass of earth = 6 * 10²⁴kg]

0 Follower 2 Views

Vishal Baghel

Contributor-Level 10

$T = 2 π \sqrt[]{\frac{r^{3}}{G M_{e}}}$

$T_{B} - T_{A} = \frac{2 π}{\sqrt[]{G M_{e}}} (r_{B}^{3 / 2} - r_{A}^{3 / 2}) = \frac{2 * 3.14}{\sqrt[]{6.67 * 1 0^{- 11} * 6 * 1 0^{24}}} [{(8 * 1 0^{6})}^{\frac{3}{2}} - {(7 * 1 0^{6})}^{\frac{3}{2}}]$

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

The minimum and maximum distance of a satellite from the centre of the earth are 2R and 4R, respectively, where R is the radius of earth and M is the mass of earth. The radius of curvature at the point of maximum distance is

0 Follower 4 Views

alok kumar singh

Contributor-Level 10

$\frac{1}{2} m V_{a}^{2} - \frac{G M m}{2 x}$

= $\frac{1}{2} m \frac{V_{a}^{2}}{4} - \frac{G M m}{4 x}, V_{a} = \sqrt[]{\frac{2}{3} \frac{G M}{x}}$

ROC at point – B

$R O C = \frac{V_{b}^{2}}{a ⊥} = \frac{\frac{2 G M}{3 R} * \frac{1}{4}}{\frac{G M}{{(4 R)}^{2}}} = \frac{8 R}{3}$

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

A satellite is moving around a planet of radius R in a circular orbit of radius r. The speed of the satellite is v. Find the acceleration due to gravity on the surface of the planet.

0 Follower 9 Views

Vishal Baghel

Contributor-Level 10

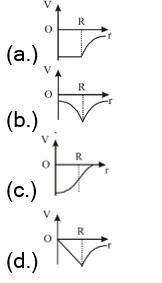
v = √ (GM/r) (orbital speed)
⇒ GM = v²r ⇒ (GM/R²) = (v²r/R²) ⇒ g = (v²r/R²)

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

The mass density of a planet of radius $R$ varies with the distance $r$ from its centre as $ρ (r) = ρ_{0} (1 - \frac{r^{3}}{R^{3}})$ . Then the gravitational field is maximum at:

0 Follower 4 Views

Raj Pandey

Contributor-Level 9

$g = \frac{G M_{in}}{r^{2}}$ , where $M_{in} = \int_{0}^{r} ? ρ 4 π x^{2} \cdot d x$

$\begin{array}{r} M_{in} = 4 π ρ_{0} \int_{0}^{r} ? ? (1 - \frac{x^{3}}{R^{3}}) x^{2} d x = 4 π ρ_{0} (\frac{r^{3}}{3} - \frac{r^{6}}{6 R^{3}}) \\ ∴ g = \frac{4 π G ρ_{0}}{6} (2 r - \frac{r^{4}}{R^{3}}) \end{array}$ $_{}_{}^{}^{}$

For $g$ to be maximum or minimum or constant $\frac{d g}{d r} = 0 \Rightarrow 2 - \frac{4 r^{3}}{R^{3}} = 0 \Rightarrow r = \frac{R}{2^{1 / 3}}$ $\frac{}{} \frac{^{}}{^{}} \frac{}{^{}}$

0 0

New answer posted

2 months ago

Physics Gravitation Class 11th

In free space, two particles of mass m each are initially both at rest at a distance a from each other. They start moving towards each other due to their mutual gravitational attraction. The time after which the distance between them has reduced to a/2 is

0 Follower 5 Views

Vishal Baghel

Contributor-Level 10

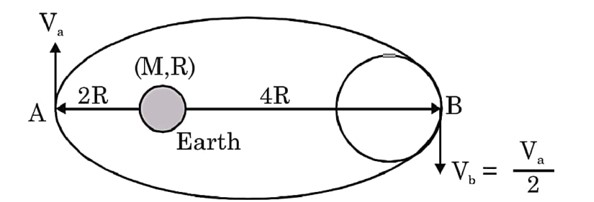
Let the origin be at the CM of the particles, let the initial positions of the particles be x = a/2 and x = -a/2 and let the instantaneous positions of the particles be x = r and x = -r
Let the instantaneous velocity of each particle be v
Let the time after which the distance between the particles has reduced to a/2 be T
Then, for the particle that was initially at x = -a/2,
(Gm²/ (2r)²) = -m (vdv/dr) ⇒ (Gm/r²) = - (4vdv/dr) ⇒ -4∫vdv = Gm∫ (dr/r²)
[v is negative because the velocity is towards the –X direction]
dr/dt = -√ (Gm/2) (1/r - 2/a)¹? ²
⇒ ∫ (a/2)^ (a/4) (r/√ (a-2r)dr = -√ (Gm/2a) ∫? dt
⇒ ∫ (a/2)^ (a/4

...more

0 0

Get authentic answers from experts, students and alumni that you won't find anywhere else

On Shiksha, get access to

65k Colleges
1.2k Exams
679k Reviews
1800k Answers

Community GuidelinesUser Points System

QuestionsDiscussionsTags

Need guidance on career and education? Ask our experts

Your Question

Physics Gravitation

Questions

Discussions

Active Users

Followers

All

Discussions

Unanswered Questions

Share Your College Life Experience