Class 12th
Get insights from 12k questions on Class 12th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 12th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
7 months agoContributor-Level 10
Let x and y meters be the length and breath of the rectangular base of the tank respectively.
Then, volume V of the tank is
V = length * depth * breath.
V = 2xy = 8m3(given).
Let 't' be the total cost of building the tank.
Then, t = cost of base + cost of sides.
= 70xy + 45[4x+4y] {there are four sides.
= 70xy + 180x+ 180y.
=
So,
And
At
x = ± 2
x = 2, (x = length and it cannot be negative)
At x = 2,
x = 2 is point of maxima.
Hence, minimum cost = = 280 + 360 + 360 = 1000.
New answer posted
7 months agoContributor-Level 10
The given equation of the ellipse is (1)
Let the major axis be along x-axis so, vertex is at
Let ΔABC be the isosceles triangle inscribed on the
ellipse with one vertex C at (a, 0).
Then, let A have Co-ordinate (x0, yo) from figure.
So, Co-ordinate of B = (x0, y0)
As A and B lies on the ellipse, from equation (i),




New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
It's worth noting that when the temperature drops, the values of Henry's law constant (KH) rise. Because of this, the solubility of oxygen in water increases with decreasing temperature at a given pressure. As a result, the presence of more oxygen at lower temperatures makes aquatic organisms feel more at ease in cold water than in warm water.
New answer posted
7 months agoContributor-Level 10
We have, f(x) =
{
At
So we have three disjoint internal i.e.,
When,
So, f(x) is increasing.
When
So, f(x) is decreasing.
When
f(x) =
So, f(x) is increasing.
f(x) is increasing for x(∞,1) and [1, ∞] and decreasing for x[1, 1].
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
p =KHx (where p is the partial pressure of the gas in the vapour phase and x is the mole fraction of the gas in solution) is Henry's law expressed mathematically.
As a result of the aforementioned equation, "the lower the solubility of the gas in the liquid, the greater the value of Henry's law constant KH at a given pressure."
New answer posted
7 months agoContributor-Level 10
We have, f(x)=
So,
Now,
And, as cos x lies in [1, 1].
So, (i) for increasing, f(x) ≥ 0.
cosx ≥ 0.
x lies in Ist and IVth quadrant.
i.e., f(x) is increasing for and
(ii) for decreasing, f(x) ≤ 0.
cosx ≤ 0.
x lies in IInd and IIIrd quadrant.
i.e., f(x) is decreasing for .
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
The number of moles of solute dissolved in one litre of solution is the molarity of a solution, which is defined as "the number of moles of solute dissolved in one litre of solution." Because volume is affected by temperature and changes with it, the molarity will also change as the temperature changes.
Other concentration words, such as mass percentage, ppm, mole fraction, and molality, are based on the mass-to-mass relationship of the solute and solvent in a binary solution. Because mass does not vary as a function of temperature, these concentration terms do not chan
New answer posted
7 months agoContributor-Level 10
We have
Slope of the normal at any point is
The equation of the normal at a given point is given by,
Now, the perpendicular distance of the normal from the origin is
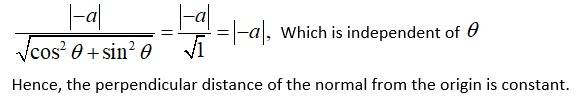
New answer posted
7 months agoContributor-Level 10
This is a short answer type question as classified in NCERT Exemplar
The solubility rule "like dissolves like" is based on the intermolecular forces of that exist in solution as follows:
If the intermolecular interactions in both components are similar, a substance (solute) dissolves in a solvent (ie. solvent and solute particles or molecules). When polar solutes dissolve in polar solvents and non-polar solutes dissolve in non-polar solvents, this is a regular occurrence.
New answer posted
7 months agoContributor-Level 10
Equation of the curve is
Now, the slope of the normal at point is
Equation of the normal at is
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 684k Reviews
- 1800k Answers
