Sequences and Series

19. Let a and d be the first term and the common difference of an A.P.

Then, given a_p = $\frac{1}{q}$

a+(p – 1)d = $\frac{1}{q}$ --------(1)

and a_q = $\frac{1}{p}$

a+(q – 1)d = $\frac{1}{p}$ ---------(2)

Subtracting eqn (2) from (1) we get,

a+(p – 1)d – [a+(q – 1)d]= $\frac{1}{q}-\frac{1}{p}$

a+(p – 1)d– a–(q– 1)d= $\frac{p-q}{pq}$

[(p – 1)–(q – 1)]d= $\frac{p-q}{pq}$

[p – 1 – q+1]d= $\frac{p-q}{pq}$

[p – q]d= $\frac{p-q}{pq}$ .

d= $\frac{1}{pq}$ .

Putting d= $\frac{1}{pq}$ in eqn (1) we get,

$a+(p-1)\frac{1}{pq}=\frac{1}{q}$ .

$a+\frac{1}{pq}-\frac{1}{pq}=\frac{1}{q}$

$a+\frac{1}{q}-\frac{1}{pq}=\frac{1}{q}$

$a=\frac{1}{q}-\frac{1}{q}+\frac{1}{pq}$ $a=\frac{1}{pq}$ .

So, sum of first pq terms,

$S_{pq}=\frac{pq}{2}\left[2*\frac{1}{pq}+(pq-1)\frac{1}{pq}\right]$

= $\frac{pq}{2}*\frac{1}{pq}[2+pq-1]$ .

= $\frac{1}{2}[pq+1]$

18. Let the sum of n farms of the A.P –6, $-\frac{11}{2}$ , –5, …. gives –25.

Then, 

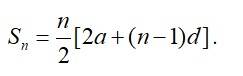
From the given A.P.

a= –6

d= – $\frac{11}{2}-(-6)=-\frac{11}{2}+6=-\frac{11+12}{2}=\frac{1}{2}$

So, –25= $\frac{n}{2}\left[2*(-6)+(n-1)\left(\frac{1}{2}\right)\right]$

–25 * 2=n $\left[-12+\frac{n-1}{2}\right]$

–50=n $\left[\frac{-12*2+(n-1)}{2}\right]$

–50=n $\left[\frac{-24+n-1}{2}\right]$

–50 * 2 =n[n – 25]=n² – 25n

n² – 25n+100=0.

n² – 5n – 20n+100=0

n(n – 5) – 20(n – 5)=0

(n – 5)(n – 20)=0

So, n=5 and n=20.

When n=5

$S_5=\frac{5}{2}\left[-12+(5-1)\frac{1}{2}\right]=\frac{5}{2}\left[-12+4*\frac{1}{2}\right]=\frac{5}{2}[-12+2]=\frac{5}{2}*(-10)$ = –25.

When n=20

$S_{20}=\frac{20}{2}\left[-12+(20-1)\frac{1}{2}\right]=10\left[-12+\frac{19}{2}\right]$ = $-120+\frac{19*10}{2}$ = –120 + 19 * 5 = –120 + 95 = –25.

17. Given, a=2

Let A1, A2, A3, A4, A5, A6, A1, A6, A7, A10 be the first ten terms. So, A1=a.

Given A1+A2+A3+A4+A5= $\frac{1}{4}$  (A6+A1+A8+A1+A10)

a+ (a+d)+ (a+2d)+ (a+3d)+ (a+4d)

= $\frac{1}{4}$  [ (a+5d)+ (a+6d)+ (a+7d)+ (a+8d)+ (a+9d)]

5a+10d= $\frac{1}{4}$  [5a+35d].

4 [5a+10d]=9a+35d.

20a+40d=5a+35d.

40d – 35d=5a – 20a

5d= –15a

d= –3a

d= –3 * 2 [as a=2]

d= –6

So, A₂₀=a+ (20 – 1)d

=2+19 * (–6)

=2 – 114

= –112.

16. Sum of all natural number between 100 and 1000 which are multiple of 5.

=105+110+115+ … +995.

So, a=105.

a=110 – 105=5.

As the last term is 995 which is the nthterm,

a+ (n – 1)d =995.

105+ (n – 1) * 5 =995.

(n – 1) * 5=995 – 105.

(n – 1)5 =890

n – 1 = $\frac{890}{5}=178$

n =178+1

n =179

So, required sum S_n $\frac{n}{2}$ (a+l); l=last term.

$=\frac{179}{2}(105+995)$

$=\frac{179}{2}*1100$

= 179 * 550

=98450.

15. Sum of odd integers from 1 to 2001

=1+3+5+ … +2001

So, a=1

d=3 – 1=2

? For n^th term,

a_n=a+ (n – 1)d.

? the last n^th term is 2001,

2001 =1+ (n – 1)2.

(n – 1)2 =2001 – 1

n – 1= $\frac{2000}{2}=1000$

n =1000+1

n =1001.

? Sum of n terms, S_n= $\frac{n}{2}$  (a + l); l = last term.

? Required sum = $\frac{1001}{2}(1+2001)=\frac{1001}{2}*20021001*1001$ =1002001

14. Given, a₁=1=a₂.

a_n=a_{n – 1}+a_{n – 2},n>2.

We need to find, $\frac{a_{n+1}}{n}$

Putting n=3,4,5,6 in an=an – 1+an – 2 we have,

a₃=a_{3 – 1}+a_{3 – 2}=a₂+a₁=1+1=2.

a₄=a_{4 – 1}+a_{4 – 2}=a₃+a₂=2+1=3.

a₅=a_{5 – 1}+a_{5 – 2}=a₄+a₃=3+2=5.

a₆=a_{6 – 1}+a_{6 – 2}=a₅+a₄=5+3=8.

Now, to find $\frac{a_{n+1}}{n}$ ,

Substitute n=1,2,3,4,5.

$\frac{a_{1+1}}{a_1}=\frac{a_2}{a_1}=\frac{1}{1}=1$

$\frac{a_{2+1}}{a_2}=\frac{a_3}{a_2}=\frac{2}{1}=2$

$\frac{a_{3+1}}{a_3}=\frac{a_4}{a_3}=\frac{3}{2}$

$\frac{a_{4+1}}{a_4}=\frac{a_5}{a_4}=\frac{5}{3}$

$\frac{a_{5+1}}{a_5}=\frac{a_6}{a_5}=\frac{8}{5}$ .

13. Given,

a₁=a₂=2.

a_n=a_{n – 1} – 1

Putting n=3,4,5.

a₃=a_{3 – 1} – 1=a_{3 – 1} – 1=a₂ – 1=2 – 1=1

a₄=a_{4 – 1} – 1=a₃ – 1=1 – 1=0

a₅=a_{5 – 1} – 1=a₄ – 1=0 – 1= –1 .

Hence the first five forms of the sequence are 2,2,1,0, –1.

And the series is 2+2+1+0+ (–1)+ ….

12. Given, a₁= –1,

$a_n=\frac{a_{n-1}}{n},n\ge 2$

Putting n=2,3,4,5 we get,

$a_2=\frac{a_{2-1}}{2}=\frac{a_1}{2}=-\frac{1}{2}$

$a_3=\frac{a_{3-1}}{3}=\frac{a_2}{3}=\frac{-1/2}{3}=-\frac{1}{6}$

$a_4=\frac{a_{4-1}}{4}=\frac{a_3}{4}=\frac{-1/6}{4}=-\frac{1}{24}.$

$a_5=\frac{a_{5-1}}{5}=\frac{a_4}{5}=\frac{-1/24}{5}=-\frac{1}{120}$ .

So the first five terms of the sequence are –1, $-\frac{1}{2},-\frac{1}{6},-\frac{1}{24}$ and $-\frac{1}{120}$ .

And the series is $(-1)+\left(-\frac{1}{2}\right)+\left(-\frac{1}{6}\right)+\left(-\frac{1}{24}\right)+\left(-\frac{1}{120}\right)+\dots$ .

11. Given, a₁=3

a_n=3a_{n – 1}.+2  "n>1.

Putting n=2,3,4,5 we get,

a₂=3a_{2 – 1}+2=3a₁+2=3 * 3+2=9+2=11

a₃=3a_{3 – 1}+2=3a₂+2=3 * 11+2=33+2=35

a₄=3a_{4 – 1}+2=3a₃+2=3 * 35+2=105+2=107.

a₅=3a_{5 – 1}+2=3a₄+2=3 * 107+2=321+2=323.

Hence, the first five terms of the sequence are 3,11,35,107,323.

And the series is 3+11+35+107+323+ …

10.$a_n=\frac{x(x-2)}{x+3}$ .

Put n=20,

$a_{20}=\frac{20(20-2)}{20+3}=\frac{20*18}{23}=\frac{360}{23}$