Class 11th
Get insights from 8k questions on Class 11th, answered by students, alumni, and experts. You may also ask and answer any question you like about Class 11th
Follow Ask QuestionQuestions
Discussions
Active Users
Followers
New answer posted
4 months agoContributor-Level 10
Bohr's model is too simple for atoms beyond hydrogen. In multi-electron atoms like helium, it fails because it ignores a couple of aspects. First is the electron-to-electron repulsion, and second is the shielding effect, where inner electrons reduce the nuclear pull on outer ones. Due to both, orbitals with the same principal quantum number don't have the same energy. Bohr's model of atom assumes that it should have the same energy.
New answer posted
4 months agoContributor-Level 10
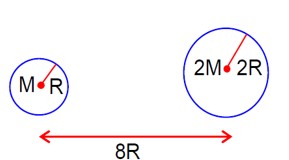
We have to find the point where the gravitational field must be zero.
EG = 0
GM/x² = G (9M)/ (8R-x)²
1/x² = 9/ (8R-x)²
8R - x = 3x => x = 2R
Potential at A (surface of first planet), VA = -GM/R - G (9M)/7R = -16GM/7R
Potential at point x, Vx = -GM/x - G (9M)/ (8R-x) = -GM/2R - G (9M)/6R = -2GM/R
ΔV = Vx - VA = -2GM/R - (-16GM/7R) = (-14+16)GM/7R = 2GM/7R
Using conservation of mechanical energy
ΔKE = ΔU = mΔV
½mv² = m (2GM/7R)
v² = 4GM/7R
v = √ (4GM/7R) => a = 4
New answer posted
4 months agoContributor-Level 10
Loss in elastic potential energy = Gain in KE
½ (YA/L)x² = ½mv²
0.5 * (0.5*10? * 10? / 0.1) * (0.04)² = 20*10? ³ v²
0.5 * (5*10²) * 1.6*10? ³ = 20*10? ³ v²
0.4 = 20*10? ³ v²
v² = 20 => v = √20 ≈ 4.47 m/s
(Re-checking calculations)
0.5 * ( (0.5e9 * 1e-6) / 0.1) * (0.04)^2 = 0.5 * (5e2) * 1.6e-3 = 4.
0.5 * 20e-3 * v^2 = 10e-3 v^2
4 = 10e-3 v^2
v^2 = 400 => v = 20 m/s
New answer posted
4 months agoContributor-Level 9
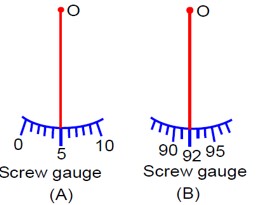
Difference in Reading = Positive Zero Error - Negative Zero Error
= (+5) - [- (100-92)]
= 5 - [-8]
= 13
New answer posted
4 months agoContributor-Level 10
-dT/dt = K [T - Ts]
- (61-59)/4 = K [ (61+59)/2 - 30]
-0.5 = K [60 - 30] = 30K
So, K = -1/60 min? ¹
Again - (51-49)/t = K [ (51+49)/2 - 30]
-2/t = (-1/60) [50-30] = -20/60 = -1/3
t = 6 min
New answer posted
4 months agoContributor-Level 9
From conservation of momentum:
2*4 = 2v? + mv?
Given v? = 1 m/s (interpreted from intermediate steps)
8 = 2 (1) + mv?
mv? = 6 . (i)
From coefficient of restitution (e=1 for elastic collision):
e = (v? - v? )/ (u? - u? )
1 = (v? - v? )/ (4 - 0)
-1 = (v? - v? )/ (0 - 4) (as written in the image)
⇒ 4 = v? - 1
⇒ v? = 5 . (ii)
Put (2) in (1), m (5) = 6
m = 1.2kg
New answer posted
4 months agoContributor-Level 10
E = ½mω²a² . (i)
When KE = 3E/4, PE = E - KE = E/4
E/4 = ½mω²y² . (ii)
Divide eq? (i) by eq? (ii) we get
4 = a²/y² => y = a/2
New answer posted
4 months agoContributor-Level 10
h = u²/2g, u = √2gh
Now, S = h/3
S = ut + ½at²
h/3 = √2ght - ½gt²
t² - 2√ (2h/g)t + 2h/3g = 0
Using quadratic formula for t:
t = ( 2√ (2h/g) ± √ (8h/g) - 4 (2h/3g) / 2
t = √ (2h/g) ± √ (2h/g - 2h/3g) = √ (2h/g) ± √ (4h/3g)
t? /t? = (√ (2h/g) - √ (4h/3g) / (√ (2h/g) + √ (4h/3g)
t? /t? = (√2 - √ (4/3) / (√2 + √ (4/3) = (√6 - 2)/ (√6 + 2)
(Note: There is a calculation error in the provided solution. Re-evaluating the physics.)
h/3 = (√2gh)t - ½gt²
(g/2)t² - (√2gh)t + h/3 = 0
t = (√2gh ± √ (2gh - 4 (g/2) (h/3)/g = (√2gh ± √ (4gh/3)/g
t? /t? = (√2gh - 2√gh/√3)/ (√2gh + 2√gh/√3)
New answer posted
4 months agoContributor-Level 9
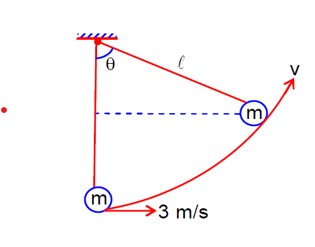
(1/2)mu² = (1/2)mv² + mgl (1-cosθ)
⇒ v² = u² - 2gl (1-cosθ)
⇒ v² = 3² - 2*10*0.5* (1 - 1/2)
⇒ v² = 9 - 5 = 4
v = 2m/s
New answer posted
4 months agoContributor-Level 9
ω = √k_eq/μ [μ = (m? )/ (m? +m? ) (Reduced mass)]
k_eq = (k * 4k)/ (k+4k) = 4k/5
ω = √ (4k/5) / (m? / (m? +m? )
= √ (4*20/5) / (0.2*0.8)/ (0.2+0.8)
= √ (16/0.16)
= 10 rad/s
Taking an Exam? Selecting a College?
Get authentic answers from experts, students and alumni that you won't find anywhere else
Sign Up on ShikshaOn Shiksha, get access to
- 66k Colleges
- 1.2k Exams
- 681k Reviews
- 1800k Answers