- Applications of Integrals Short Answer Type Questions
- Applications of Integrals Long Answer Type Questions
- Applications of Integrals Objective Type Questions
Applications of Integrals Short Answer Type Questions
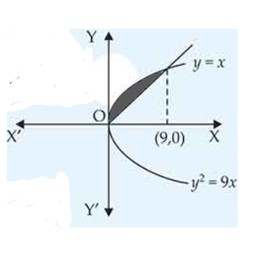
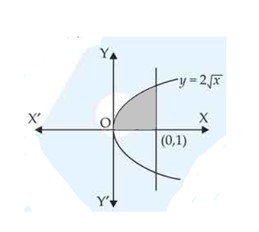
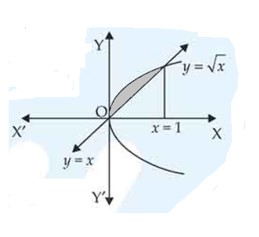
| 1. Find the area of the region bounded by the curves and . |
| Sol: |
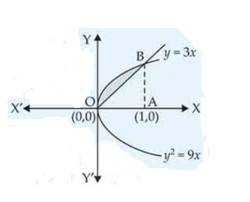
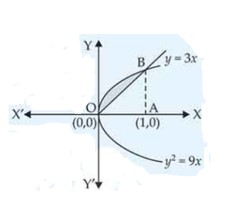
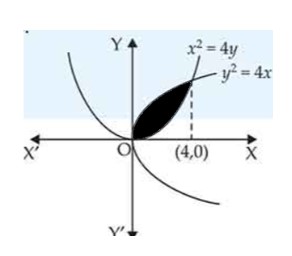
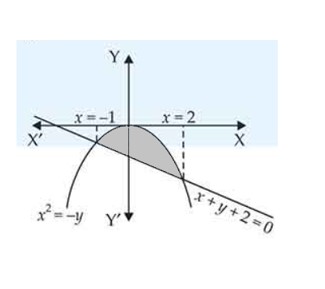
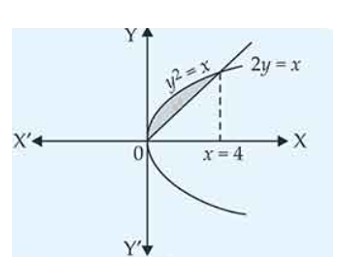
| 2. Find the area of the region bounded by the parabolas and . |
| Sol:
|
Commonly asked questions
Find the area of the region bounded by the curves and .
This is a short answer type question as classified in NCERT Exemplar
Find the area of the region included between the curves and .
This is a short answer type question as classified in NCERT Exemplar
Find the area of the region bounded by the parabolas and .
This is a short answer type question as classified in NCERT Exemplar
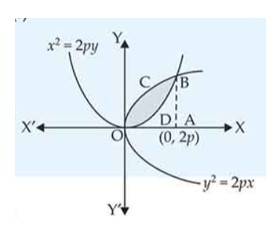
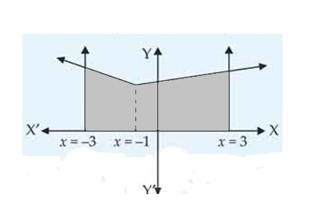
Find the area of the region bounded by the curves , , and .
This is a short answer type question as classified in NCERT Exemplar
Find the area of the region bounded by the curves and .
This is a short answer type question as classified in NCERT Exemplar
Find the area of the region enclosed by the parabola and the line .
This is a short answer type question as classified in NCERT Exemplar
Find the area of the region bounded by the line and the parabola .
This is a short answer type question as classified in NCERT Exemplar
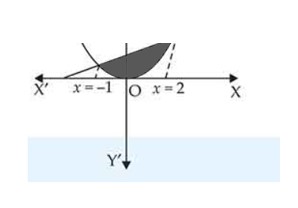
Sketch the region and the x-axis. Find the area of the region using integration.
This is a short answer type question as classified in NCERT Exemplar
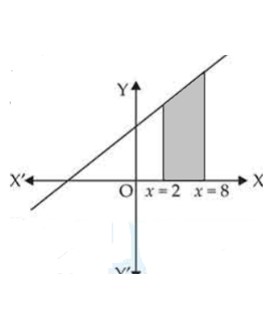
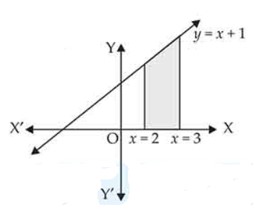
Calculate the area under the curve included between the lines and .
This is a short answer type question as classified in NCERT Exemplar
Using integration, find the area of the region bounded by the line , the x-axis, and the lines and .
This is a short answer type question as classified in NCERT Exemplar
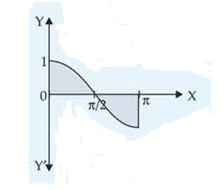
Draw a rough sketch of the curve in the interval . Find the area under the curve and between the lines and .
This is a short answer type question as classified in NCERT Exemplar
Determine the area under the curve included between the lines and .
This is a short answer type question as classified in NCERT Exemplar
Find the area of the region bounded by and .
This is a short answer type question as classified in NCERT Exemplar
Find the area enclosed by the curve and the straight line .
This is a short answer type question as classified in NCERT Exemplar
Find the area bounded by the curves and in the first quadrant and the x-axis.
This is a short answer type question as classified in NCERT Exemplar
Applications of Integrals Long Answer Type Questions
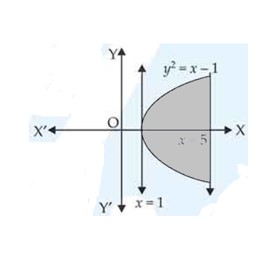
| 1. Find the area of the region bounded by the curves and . |
| Sol. |
| 2. Find the area bounded by the curve between and . |
| Sol.
|
Commonly asked questions
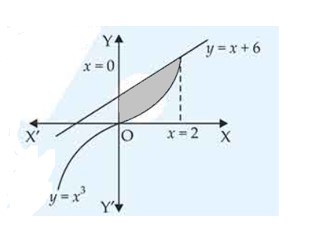
Compute the area bounded by the lines , , and .
This is a long answer type question as classified in NCERT Exemplar
Find the area of the region bounded by the curves and .
This is a long answer type question as classified in NCERT Exemplar
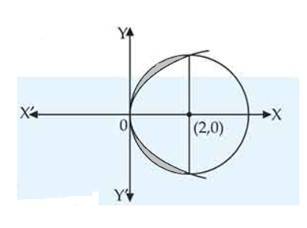
Find the area bounded by the curve between and
This is a long answer type question as classified in NCERT Exemplar
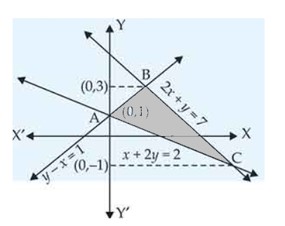
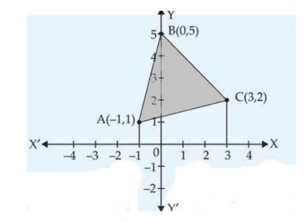
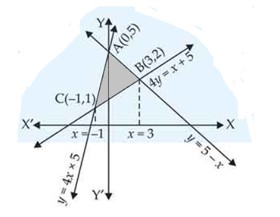
Find the area of the region bounded by the triangle whose vertices are , , and , using integration.
This is a long answer type question as classified in NCERT Exemplar
Draw a rough sketch of the region . Also, find the area of the region sketched using the method of integration.
This is a long answer type question as classified in NCERT Exemplar
Find the area bounded by the lines , , and .
This is a long answer type question as classified in NCERT Exemplar
Find the area bounded by the curve and the x-axis from to .
This is a long answer type question as classified in NCERT Exemplar
Draw a rough sketch of the given curve , , , and find the area of the region bounded by them using integration.
This is a long answer type question as classified in NCERT Exemplar
Applications of Integrals Objective Type Questions
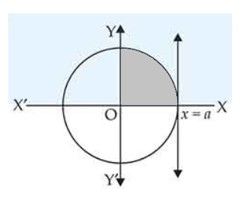
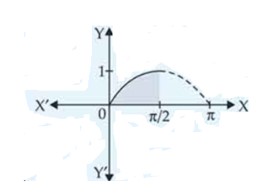
| 1. The area of the region bounded by the y-axis, and , is: (A) sq. units (B) +1sq. units (C) sq. units (D) sq. units |
| Sol. |
| 2. The area of the region bounded by the curve and the straight line is: (A) sq. units (B) sq. units (C) sq. units (D) sq. units |
| Sol. |
Commonly asked questions
The area of the region bounded by the y-axis, and , is:
(A) sq. units
(B) +1sq. units
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
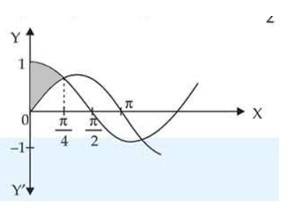
The area of the region bounded by the curve and the straight line is:
(A) sq. units
(B) sq. units
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
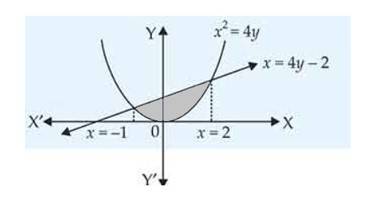
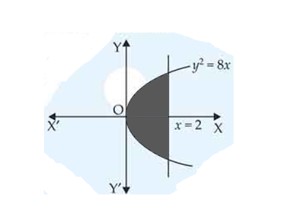
The area of the region bounded by the curve and the x-axis is:
(A) 8 sq. units
(B) sq. units
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
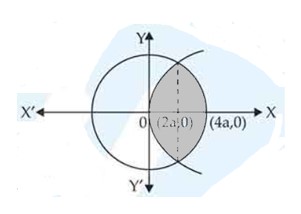
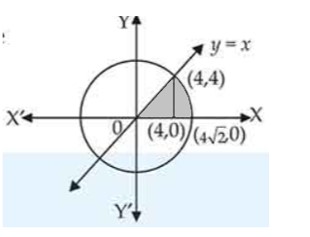
Area of the region in the first quadrant enclosed by the x-axis, the line y = x and the circle is:
(A) sq. units
(B) sq. units
(C) sq. units
(D) 24 sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
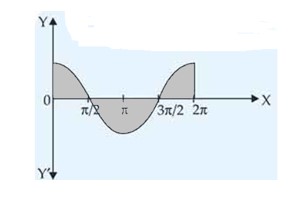
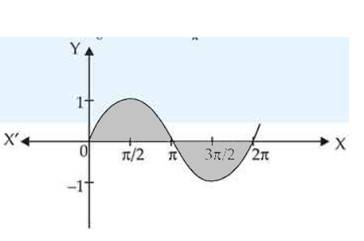
The area of the region bounded by the curve y = cosx between and is:
(A) 2 sq. units
(B) 4 sq. units
(C) 3 sq. units
(D) 1 sq. unit
This is an Objective Type Questions as classified in NCERT Exemplar
The area of the region bounded by the parabola and the straight line is:
(A) sq. units
(B) 1 sq. unit
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
The area of the region bounded by the curve between the ordinates , , and the x-axis is:
(A) 2 sq. units
(B) 4 sq. units
(C) 3 sq. units
(D) 1 sq. unit
This is an Objective Type Questions as classified in NCERT Exemplar
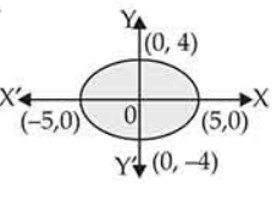
The area of the region bounded by the ellipse is:
(A) sq. units
(B) sq. units
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
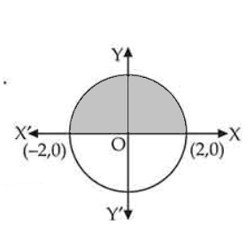
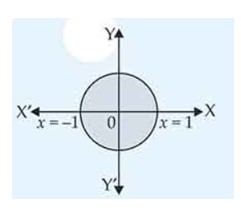
The area of the region bounded by the circle is:
(A) sq. units
(B) sq. units
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
The area of the region bounded by the curve and the lines and is:
(A) sq. units
(B) sq. units
(C) sq. units
(D) sq. units
This is an Objective Type Questions as classified in NCERT Exemplar
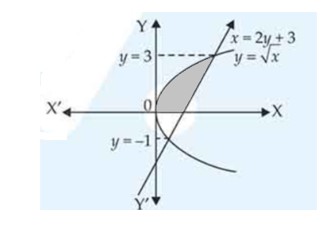
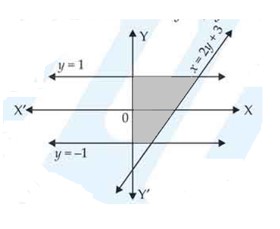
The area of the region bounded by the curve x = 2y + 3 and the y lines. y = 1 and y = –1 is
(A) 4 sq units
(B) sq units
(C) 6 sq units
(D) 8 sq unit
This is an Objective Type Questions as classified in NCERT Exemplar
Maths NCERT Exemplar Solutions Class 12th Chapter Eight Exam