The distance of the point ( α , β , γ ) from the y-axis is (A) β (B) γ (C) β 2 + γ 2 (D) α 2 + γ 2

This is a Objective Type Questions as classified in NCERT Exemplar The given point is (α, β, γ) Any point on y−axis=(0, β, 0) ∴Required distance=(α−0)2+(β−β)2+(δ−0)2 = α 2 + γ 2 H e n c e , t h e c o r r e c t o p t i o n i s ( d ) .

The distance of the plane from the origin is: (A) 1 (B) 7 (C) 1 7 (D) None of these

This is a Objective Type Questions as classified in NCERT Exemplar G i v e n t h a t r → . ( 2 7 i ^ + 3 7 j ^ − 6 7 k ^ ) = 1 So, the distance of the given plane from the origin is = | − 1 ( 2 7 ) 2 + ( 3 7 ) 2 + ( − 6 7 ) 2 | = | − 1 4 4 9 + 9 4 9 + 3 6 4 9 | = 1 1 = 1 H e n c e , t h e c o r r e c t o p t i o n i s ( a ) .

The angle between the line r → = ( 5 i ^ + 3 j ^ + 7 k ^ ) + λ ( 2 i ^ − j ^ + k ^ ) and the plane r → = 3 i ^ − 4 j ^ − 4 k ^ + 5 = 0 is s i n − 1 ( 5 / 2 √ 9 1 ) . .

This is a True or False Type Questions as classified in NCERT Exemplar E q u a t i o n o f l i n e i s r → = ( 5 i ^ − j ^ − 4 k ^ ) + λ ( 2 i ^ − j ^ + k ^ ) a n d t h e e q u a t i o n o f p l a n e i s r → . ( 3 i ^ − 4 j ^ − k ^ ) + 5 = 0 H e r e , b 1 → = 2 i ^ − j ^ + k ^ a n d n 2 → = 3 i ^ − 4 j ^ − k ^ ∴ s i n θ = b 1 → n 2 → | b 1 → | | n 2 → | ⇒ s i n θ = ( 2 i ^ − j ^ + k ^ ) . ( 3 i ^ − 4 j ^ − k ^ ) 4 + 4 + 1 9 + 1 6 + 1 = 6 + 4 − 1 6 2 6 = 9 6 2 6 ⇒ s i n θ = 9 2 3 9 w h i c h i s f a l s e . H e n c e , t h e g i v e n s t a t e m e n t i s F a l s e .

The angle between the planes r→⋅(2i^−3j^+k^)=1 and r→⋅(i^−j^)=4 is c o s − 1 ( 5 √ 5 8 ) .

This is a True or False Type Questions as classified in NCERT Exemplar T h e g i v e n p l a n e a r e r → . ( 2 i ^ − 3 j ^ + k ^ ) = 1 a n d r → . ( i ^ − j ^ ) = 4 H e r e , b 1 → = 2 i ^ − 3 j ^ + k ^ a n d n 2 → = i ^ − j ^ S o , c o s θ = b 1 → n 2 → | b 1 → | | n 2 → | ⇒ c o s θ = ( 2 i ^ − 3 j ^ + k ^ ) . ( i ^ − j ^ ) 4 + 9 + 1 1 + 1 = 2 + 3 1 4 2 = 5 2 8 ∴ θ = c o s − 1 ( 5 2 8 ) w h i c h i s f a l s e . H e n c e , t h e g i v e n s t a t e m e n t i s F a l s e .

Find the length and the foot of the perpendicular from the point ( 1 , 3 2 , 2 ) to the plane 2 x − 2 y + 4 z + 5 = 0 .

This is a long answer type question as classified in NCERT Exemplar Given plane is 2x−2y+4z+5=0 and the given points is(1, 32, 2) D ' r a t i o s o f t h e n o r m a l t o t h e p l a n e a r e 2 , − 2 , 4 So, the? equation of line passing through (1, 32, 2) and whose d'ratios are equal to the D ' r a t i o s o f t h e n o r m a l t o t h e p l a n e i . e . , 2 , − 2 , 4 i s x − 1 2 = y − 3 2 − 2 = z − 2 4 = λ ∴Any point in the plane is 2λ+1, −2λ+32, 4λ+2 Since, the point lies in the plane, then 2 ( 2 λ + 1 ) − 2 ( − 2 λ + 3 2 ) + 4 ( 4 λ + 2 ) + 5 = 0 ⇒ 4 λ + 2 + 4 λ − 3 + 1 6 λ + 8 + 5 = 0 ⇒ 2 4 λ + 1 2 = 0 ∴ λ = − 1 2 So, the coordinates of the point in the plane are 2 ( − 1 2 ) + 1 , − 2 ( − 1 2 ) + 3 2 , 4 ( − 1 2 ) + 2 i . e . , 0 , 5 2 , 0 H e n c e , t h e f o o t o f t h e p e r p e n d i c u l a r i s ( 0 , 5 2 , 0 ) a n d t h e r e q u i r e d l e n g t h = ( 1 − 0 ) 2 + ( 3 2 − 5 2 ) 2 + ( 2 − 0 ) 2 = 1 + 1 + 4 = 6 u n i t s

The direction cosines of the vector ( 2 i ^ + 2 j ^ − k ^ ) are __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar L e t a → = 2 i ^ + 2 j ^ − k ^ d i r e c t i o n r a t i o s o f a → a r e 2 , 2 , − 1 ∴the direction cosines are 24+4+1, 24+4+1, −14+4+1 ⇒ 2 3 , 2 3 , − 1 3 Hence, the direction cosines of the given vector are 23, 23, −13.

The vector equation of the line x − 5 3 = y + 4 7 = z − 6 2 is __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar T h e g i v e n e q u a t i o n i s x − 5 3 = y + 4 7 = z − 6 2 H e r e , a → = ( 5 i ^ − 4 j ^ + 6 k ^ ) a n d b → = ( 3 i ^ + 7 j ^ + 2 k ^ ) E q u a t i o n o f t h e l i n e i s r → = a → + b → λ H e n c e , t h e v e c t o r e q u a t i o n o f t h e g i v e n l i n e i s r → = ( 5 i ^ − 4 j ^ + 6 k ^ ) + λ ( 3 i ^ + 7 j ^ + 2 k ^ )

The cartesian equation of the plane r → ^ ⋅ i ^ + j ^ + k ^ = 2 is __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar G i v e n e q u a t i o n r → . ( i ^ + j ^ − k ^ ) = 2 ⇒ ( x i ^ + y j ^ + z k ^ ) . ( i ^ + j ^ − k ^ ) = 2 ⇒ x + y − z = 2 H e n c e , t h e C a r t e s i a n e q u a t i o n o f t h e p l a n e i s x + y − z = 2

Find the position vector of a point A in space such that O A → is inclined at 60º to OX and at 45° to OY and | O A → | = 10 units.

This is a short answer type question as classified in NCERT Exemplar L e t α = 6 0 0 , β = 4 5 0 a n d t h e a n g l e i n c l i n e d t o O Z a x i s b e γ . W e k n o w t h a t c o s 2 α + c o s 2 β + c o s 2 γ = 1 ⇒ c o s 2 6 0 0 + c o s 2 4 5 0 + c o s 2 γ = 1 ⇒ ( 1 2 ) 2 + ( 1 2 ) 2 + c o s 2 γ = 1 ⇒ 1 4 + 1 2 + c o s 2 γ = 1 ⇒ 3 4 + c o s 2 γ = 1 ⇒ c o s 2 γ = 1 − 3 4 = 1 4 ∴ c o s γ = ± 1 2 ⇒ c o s γ = 1 2 ( Rejecting cosγ=−12, since γ<900 ) ∴ O A → = | O A → | ( 1 2 i ^ + 1 2 j ^ + 1 2 k ^ ) = 1 0 ( 1 2 i ^ + 1 2 j ^ + 1 2 k ^ ) = 5 i ^ + 5 2 j ^ + 5 k ^ H e n c e , t h e p o s i t i o n v e c t o r o f A i s ( 5 i ^ + 5 2 j ^ + 5 k ^ ) .

Show that the lines x − 1 2 = y − 2 3 = z − 3 4 and x − 4 5 = y − 1 2 = z intersect. Also, find their point of intersection.

This is a short answer type question as classified in NCERT Exemplar T h e g i v e n e q u a t i o n s a r e x − 1 2 = y − 2 3 = z − 3 4 a n d x − 4 5 = y − 1 2 = z L e t x − 1 2 = y − 2 3 = z − 3 4 = λ ∴ x = 2 λ + 1 , y = 3 λ + 2 a n d z = 4 λ + 3 a n d x − 4 5 = y − 1 2 = z 1 = μ ∴ x = 5 μ + 4 , y = 2 μ + 1 a n d z = μ If the two lines intersect each other at one point, t h e n 2 λ + 1 = 5 μ + 4 ⇒ 2 λ − 5 μ = 3 … ( i ) 3 λ + 2 = 2 μ + 1 ⇒ 3 λ − 2 μ = − 1 … ( i i ) a n d 4 λ + 3 = μ ⇒ 4 λ − μ = − 3 … ( i i i ) S o l v i n g e q n . ( i ) a n d ( i i ) w e g e t 2 λ − 5 μ = 3 ( M u l t i p l y b y 3 ) 3 λ − 2 μ = − 1 ( M u l t i p l y b y 2 ) ⇒ 6 λ − 1 5 μ = 9 6 λ − 4 μ = − 2 ( − ) ( + ) ( + ) _ − 1 1 μ = 1 1 ∴ μ = − 1 P u t t i n g t h e v a l u e o f μ i n e q n . ( i ) w e g e t , 2 λ − 5 ( − 1 ) = 3 ⇒ 2 λ + 5 = 3 ⇒ 2 λ = − 2 ∴ λ = − 1 N o w , p u t t i n g t h e v a l u e o f λ μ i n e q n . ( i i i ) t h e n , 4 ( − 1 ) − ( − 1 ) = − 3 − 4 + 1 = − 3 − 3 = − 3 ( s a t i s f i e d ) ∴ Coordinates of the point of intersection are x = 5 ( − 1 ) + 4 = − 5 + 4 = − 1 y = 2 ( − 1 ) + 1 = − 2 + 1 = − 1 z = − 1 Hence, the given lines intersect each other at (−1,−1,−1).

Find the vector equation of the line which is parallel to the vector 3 i ^ − 2 j ^ + 6 k ^ and which passes through the point (1, –2, 3).

This is a short answer type question as classified in NCERT Exemplar W e k n o w t h a t t h e e q u a t i o n o f l i n e i s r → = a → + b → λ H e r e , a → = i ^ − 2 j ^ + 3 k ^ a n d b → = 3 i ^ − 2 j ^ + 6 k ^ ∴ E q u a t i o n o f l i n e i s r → = ( i ^ − 2 j ^ + 3 k ^ ) + λ ( 3 i ^ − 2 j ^ + 6 k ^ ) ⇒ ( x i ^ + y j ^ + z k ^ ) = ( i ^ − 2 j ^ + 3 k ^ ) + λ ( 3 i ^ − 2 j ^ + 6 k ^ ) ⇒ ( x i ^ + y j ^ + z k ^ ) − ( i ^ − 2 j ^ + 3 k ^ ) = λ ( 3 i ^ − 2 j ^ + 6 k ^ ) ⇒ ( x − 1 ) i ^ + ( y + 2 ) j ^ + ( z − 3 ) k ^ = λ ( 3 i ^ − 2 j ^ + 6 k ^ ) H e n c e , t h e r e q u i r e d e q u a t i o n i s ( x − 1 ) i ^ + ( y + 2 ) j ^ + ( z − 3 ) k ^ = λ ( 3 i ^ − 2 j ^ + 6 k ^ ) .

Find the angle between the lines r → = ( 3 i ^ + 2 j ^ + 6 k ^ ) + λ ( 2 i ^ + j ^ + 6 k ^ ) and r → = ( 2 i ^ + 5 k ^ ) + μ ( 6 i ^ + 3 j ^ + 2 k ^ ) .

H e r e , b 1 → = 2 i ^ + j ^ + 2 k ^ a n d b 2 → = 6 i ^ + 3 j ^ + 2 k ^ ∴ c o s θ = b 1 → b 2 → | b 1 → | | b 2 → | = ( 2 i ^ + j ^ + 2 k ^ ) . ( 6 i ^ + 3 j ^ + 2 k ^ ) ( 2 ) 2 + ( 1 ) 2 + ( 2 ) 2 . ( 6 ) 2 + ( 3 ) 2 + ( 2 ) 2 = 1 2 + 3 + 4 4 + 1 + 4 3 6 + 9 + 4 = 1 9 9 4 9 = 1 9 3 . 7 = 1 9 2 1 ∴ θ = c o s − 1 ( 1 9 2 1 ) H e n c e , t h e r e q u i r e d a n g l e i s c o s − 1 ( 1 9 2 1 ) .

Maths NCERT Exemplar Solutions Class 12th Chapter Eleven: Overview, Questions, Preparation

Updated on Jul 15, 2025 10:48 IST

By Payal Gupta, Retainer

Table of content

Three-Dimensional Geometry Long Answer Type Questions
Three-Dimensional Geometry Short Answer Type Questions
Three-Dimensional Geometry Objective Type Questions
Three-Dimensional Geometry Fill in the blanks Type Questions
Three-Dimensional Geometry True or False Type Questions

Three-Dimensional Geometry Long Answer Type Questions

1. Find the foot of the perpendicular from the point (2, 3, –8) to the line $\frac{4 - x}{2} = \frac{y}{6} = \frac{1 - z}{3} .$ Also, find the perpendicular distance from the given point to the line.

Ans.

\begin{array}{l} G i v e n t h a t \frac{4 - x}{2} + \frac{y}{6} + \frac{1 - z}{3} i s t h e e q u a t i o n o f l i n e \\ \Rightarrow \frac{x - 4}{- 2} + \frac{y}{6} + \frac{z - 1}{- 3} = λ \\ ∴ C o o r d i n a t e s o f a n y point Q o n t h e l i n e a r e \\ x = - 2 λ + 4, y = 6 λ a n d z = - 3 λ + 1 \\ a n d t h e g i v e n point i s P (2, 3, - 8) \\ D i r e c t i o n r a t i o s o f P Q a r e - 2 λ + 4 - 2, 6 λ - 3, - 3 λ + 1 + 8 \\ a n d t h e D' r a t i o s o f t h e g i v e n l i n e a r e - 2, 6, - 3 . \\ I f P Q ⊥ l i n e \\ t h e n - 2 (- 2 λ + 2) + 6 (6 λ - 3) - 3 (- 3 λ + 9) = 0 \\ \Rightarrow 4 λ - 4 + 36 λ - 18 + 9 λ - 27 = 0 \\ \Rightarrow 49 λ - 49 = 0 \Rightarrow λ = 1 \\ ∴ T h e f o o t o f t h e p e r p e n d i c u l a r i s - 2 (1) + 4, 6 (1), - 3 (1) + 1 \\ i . e ., 2, 6, - 2 \\ N o w, distance P Q = \sqrt[]{{(2 - 2)}^{2} + {(3 - 6)}^{2} + {(- 8 + 2)}^{2}} \\ = \sqrt[]{9 + 36} = \sqrt[]{45} = 3 \sqrt[]{5} \\ H e n c e, t h e r e q u i r e d c o o r d i n a t e s o f t h e f o o t o f t h e p e r p e n d i c u l a r a r e 2, 6, - 2 a n d t h e \\ r e q u i r e d distance 3 \sqrt[]{5} u n i t s . \end{array}

2. Find the distance of the point (2, 4, –1) from the line $\frac{x + 5}{1} = \frac{y + 3}{4} = \frac{z - 6}{– 9} .$

Ans. $\begin{array}{l} T h e g i v e n e q u a t i o n o f l i n e i s \\ \frac{x + 5}{1} = \frac{y + 3}{4} = \frac{z - 6}{– 9} = λ a n d a n y point P (2, 4, - 1) \\ L e t Q b e a n y point o n t h e g i v e n l i n e \\ ∴ C o o r d i n a t e s o f Q a r e x = λ - 5, y = 4 λ - 3 a n d z = - 9 λ + 6 \\ a n d t h e g i v e n point i s P (2, 3, - 8) \\ D i r e c t i o n r a t i o s o f P Q a r e λ - 5 - 2, 4 λ - 3 - 4, - 9 λ + 6 + 1 \\ i . e ., λ - 7, 4 λ - 7, - 9 λ + 7 \\ a n d t h e D' r a t i o s o f t h e g i v e n l i n e a r e 1, 4, - 9 . \\ I f P Q ⊥ l i n e \\ t h e n 1 (λ - 7) + 4 (4 λ - 7) - 9 (- 9 λ + 7) = 0 \\ \Rightarrow λ - 7 + 16 λ - 28 + 81 λ - 63 = 0 \\ \Rightarrow 98 λ - 98 = 0 \Rightarrow λ = 1 \\ S o, C o o r d i n a t e s o f Q a r e 1 - 5, 4 \times 1 - 3, - 9 \times 1 + 6 \\ i . e ., - 4, 1, - 3 \\ N o w, distance P Q = \sqrt[]{{(- 4 - 2)}^{2} + {(1 - 4)}^{2} + {(- 3 + 1)}^{2}} \\ = \sqrt[]{{(- 6)}^{2} + {(- 3)}^{2} + {(- 2)}^{2}} = \sqrt[]{36 + 9 + 4} = \sqrt[]{49} = 7 \\ H e n c e, t h e r e q u i r e d distance 7 u n i t s . \end{array}$

Commonly asked questions

Find the foot of the perpendicular from the point (2, 3, –8) to the line $\frac{4 - x}{2} = \frac{y}{6} = \frac{1 - z}{3} .$ Also, find the perpendicular distance from the given point to the line.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t \frac{4 - x}{2} + \frac{y}{6} + \frac{1 - z}{3} i s t h e e q u a t i o n o f l i n e \\ \Rightarrow \frac{x - 4}{- 2} + \frac{y}{6} + \frac{z - 1}{- 3} = λ \\ ∴ C o o r d i n a t e s o f a n y point Q o n t h e l i n e a r e \\ x = - 2 λ + 4, y = 6 λ a n d z = - 3 λ + 1 \\ a n d t h e g i v e n point i s P (2, 3, - 8) \\ D i r e c t i o n r a t i o s o f P Q a r e - 2 λ + 4 - 2, 6 λ - 3, - 3 λ + 1 + 8 \\ a n d t h e D' r a t i o s o f t h e g i v e n l i n e a r e - 2, 6, - 3 . \\ I f P Q ⊥ l i n e \\ t h e n - 2 (- 2 λ + 2) + 6 (6 λ - 3) - 3 (- 3 λ + 9) = 0 \\ \Rightarrow 4 λ - 4 + 36 λ - 18 + 9 λ - 27 = 0 \\ \Rightarrow 49 λ - 49 = 0 \Rightarrow λ = 1 \\ ∴ T h e f o o t o f t h e p e r p e n d i c u l a r i s - 2 (1) + 4, 6 (1), - 3 (1) + 1 \\ i . e ., 2, 6, - 2 \\ N o w, distance P Q = \sqrt[]{{(2 - 2)}^{2} + {(3 - 6)}^{2} + {(- 8 + 2)}^{2}} \\ = \sqrt[]{9 + 36} = \sqrt[]{45} = 3 \sqrt[]{5} \\ H e n c e, t h e r e q u i r e d c o o r d i n a t e s o f t h e f o o t o f t h e p e r p e n d i c u l a r a r e 2, 6, - 2 a n d t h e \\ r e q u i r e d distance 3 \sqrt[]{5} u n i t s . \end{array}$

Find the distance of the point (2, 4, –1) from the line $\frac{x + 5}{1} = \frac{y + 3}{4} = \frac{z - 6}{– 9} .$

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n e q u a t i o n o f l i n e i s \\ \frac{x + 5}{1} = \frac{y + 3}{4} = \frac{z - 6}{– 9} = λ a n d a n y point P (2, 4, - 1) \\ L e t Q b e a n y point o n t h e g i v e n l i n e \\ ∴ C o o r d i n a t e s o f Q a r e x = λ - 5, y = 4 λ - 3 a n d z = - 9 λ + 6 \\ a n d t h e g i v e n point i s P (2, 3, - 8) \\ D i r e c t i o n r a t i o s o f P Q a r e λ - 5 - 2, 4 λ - 3 - 4, - 9 λ + 6 + 1 \\ i . e ., λ - 7, 4 λ - 7, - 9 λ + 7 \\ a n d t h e D' r a t i o s o f t h e g i v e n l i n e a r e 1, 4, - 9 . \\ I f P Q ⊥ l i n e \\ t h e n 1 (λ - 7) + 4 (4 λ - 7) - 9 (- 9 λ + 7) = 0 \\ \Rightarrow λ - 7 + 16 λ - 28 + 81 λ - 63 = 0 \\ \Rightarrow 98 λ - 98 = 0 \Rightarrow λ = 1 \\ S o, C o o r d i n a t e s o f Q a r e 1 - 5, 4 \times 1 - 3, - 9 \times 1 + 6 \\ i . e ., - 4, 1, - 3 \\ N o w, distance P Q = \sqrt[]{{(- 4 - 2)}^{2} + {(1 - 4)}^{2} + {(- 3 + 1)}^{2}} \\ = \sqrt[]{{(- 6)}^{2} + {(- 3)}^{2} + {(- 2)}^{2}} = \sqrt[]{36 + 9 + 4} = \sqrt[]{49} = 7 \\ H e n c e, t h e r e q u i r e d distance 7 u n i t s . \end{array}$

Find the length and the foot of the perpendicular from the point ( $1, \frac{3}{2}, 2$ ) to the plane $2 x - 2 y + 4 z + 5 = 0$ .

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n p l a n e i s 2 x - 2 y + 4 z + 5 = 0 a n d t h e g i v e n points i s (1, \frac{3}{2}, 2) \\ D' r a t i o s o f t h e n o r m a l t o t h e p l a n e a r e 2, - 2, 4 \\ S o, t h e ? e q u a t i o n o f l i n e passing t h r o u g h (1, \frac{3}{2}, 2) a n d w h o s e d' r a t i o s a r e e q u a l t o t h e \\ D' r a t i o s o f t h e n o r m a l t o t h e p l a n e i . e ., 2, - 2, 4 i s \frac{x - 1}{2} = \frac{y - \frac{3}{2}}{- 2} = \frac{z - 2}{4} = λ \\ ∴ A n y point i n t h e p l a n e i s 2 λ + 1, - 2 λ + \frac{3}{2}, 4 λ + 2 \\ Since, t h e point l i e s i n t h e p l a n e, t h e n \\ 2 (2 λ + 1) - 2 (- 2 λ + \frac{3}{2}) + 4 (4 λ + 2) + 5 = 0 \\ \Rightarrow 4 λ + 2 + 4 λ - 3 + 16 λ + 8 + 5 = 0 \\ \Rightarrow 24 λ + 12 = 0 ∴ λ = - \frac{1}{2} \\ S o, t h e c o o r d i n a t e s o f t h e point i n t h e p l a n e a r e \\ 2 (- \frac{1}{2}) + 1, - 2 (- \frac{1}{2}) + \frac{3}{2}, 4 (- \frac{1}{2}) + 2 i . e ., 0, \frac{5}{2}, 0 \\ H e n c e, t h e f o o t o f t h e p e r p e n d i c u l a r i s (0, \frac{5}{2}, 0) a n d t h e \\ r e q u i r e d l e n g t h = \sqrt[]{{(1 - 0)}^{2} + {(\frac{3}{2} - \frac{5}{2})}^{2} + {(2 - 0)}^{2}} \\ = \sqrt[]{1 + 1 + 4} = \sqrt[]{6} u n i t s \end{array}$

Find the equations of the line passing through the point (3, 0, 1) and parallel to the planes $x + 2 y = 0$ and $3 y - z = 0$ .

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n point i s (3, 0, 1) a n d t h e e q u a t i o n o f p l a n e s a r e \\ x + 2 y = 0 \dots (i) \\ a n d 3 y - z = 0 \dots (i i) \\ E q u a t i o n o f a n y l i n e l passing t h r o u g h (3, 0, 1) i s \\ l : \frac{x - 3}{a} = \frac{y - 0}{b} = \frac{z - 1}{c} \\ D i r e c t i o n r a t i o s o f t h e n o r m a l t o t h e p l a n e (i) a n d (i i) a r e (1, 2, 0) a n d (0, 3, - 1) \\ Since, t h e l i n e i s p a r a l l e l t o b o t h t h e p l a n e s . \\ ∴ 1 . a + 2 . b + 0 . c = 0 \Rightarrow a + 2 b + 0 c = 0 \\ a n d 0 . a + 3 . b - 1 . c = 0 \Rightarrow 0 . a + 3 b - c = 0 \\ S o, \frac{a}{- 2 - 0} = \frac{- b}{- 1 - 0} = \frac{c}{3 - 0} = λ \\ ∴ a = - 2 λ, b = λ, c = 3 λ \\ S o, e q u a t i o n o f l i n e i s \\ \frac{x - 3}{- 2 λ} = \frac{y - 0}{λ} = \frac{z - 1}{3 λ} \\ H e n c e, t h e r e q u i r e d e q u a t i o n \frac{x - 3}{- 2} + \frac{y - 0}{1} + \frac{z - 1}{3} \\ o r i n v e c t o r f o r m i s (x - 3) \hat{i} + y \hat{j} + (z - 1) \hat{k} = λ (- 2 \hat{i} + \hat{j} + 3 \hat{k}) \end{array}$

Find the equation of the plane through the points (2, 1, –1) and (–1, 3, 4), and perpendicular to the plane $x - 2 y + 4 z = 10$ .

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} E q u a t i o n o f p l a n e passing t h r o u g h t w o points (x_{1}, y_{1,} z_{1}) a n d (x_{2}, y_{2}, z_{2}) w i t h i t s n o r m a l d' r a t i o s i s \\ a (x - x_{1}) + b (y - y_{1}) + c (z - z_{1}) = 0 \dots (i) \\ I f t h e p l a n e i s passing t h r o u g h t h e g i v e n points (2, 1, - 1) a n d (- 1, 3, 4) t h e n \\ a (x_{2} - x_{1}) + b (y_{2} - y_{1}) + c (z_{2} - z_{1}) = 0 \\ \Rightarrow a (- 1 - 2) + b (3 - 1) + c (4 + 1) = 0 \\ \Rightarrow - 3 a + 2 b + 5 c = 0 \dots (i i) \\ Since, t h e r e q u i r e d p l a n e i s p e r p e n d i c u l a r t o t h e g i v e n p l a n e x - 2 y + 4 z = 10, t h e n \\ 1 . a - 2 . b + 4 . c = 10 \dots (i i i) \\ S o l v i n g (i i) a n d (i i i) w e g e t, \\ \frac{a}{8 + 10} = \frac{- b}{- 12 - 5} = \frac{c}{6 - 2} = λ \\ a = 18 λ, b = 17 λ, c = 4 λ \\ H e n c e, t h e r e q u i r e d p l a n e i s 18 λ (x - 2) + 17 λ (y - 1) + 4 λ (z + 1) = 0 \\ \Rightarrow 18 x - 36 + 17 y - 17 + 4 z + 4 = 0 \\ \Rightarrow 18 x + 17 y + 4 z - 49 = 0 \end{array}$

Find the shortest distance between the lines $\vec{r} = (8 + 3 λ) \hat{i} - (9 + 16 λ) \hat{j} + (10 + 7 λ) \hat{k}$ and $\vec{r} = 15 \hat{i} - 29 \hat{j} + 5 \hat{k} + μ (3 \hat{i} + 8 \hat{j} - 5 \hat{k})$

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n e q u a t i o n s o f l i n e s a r e \\ \vec{r} = (8 + 3 λ) \hat{i} - (9 + 16 λ) \hat{j} + (10 + 7 λ) \hat{k} \dots (i) \\ a n d \vec{r} = 15 \hat{i} - 29 \hat{j} + 5 \hat{k} + μ (3 \hat{i} + 8 \hat{j} - 5 \hat{k}) \dots (i i) \\ E q u a t i o n (i) c a n b e r e - w r i t t e n a s \\ \vec{r} = 8 \hat{i} - 9 \hat{j} + 10 \hat{k} + λ (3 \hat{i} - 16 \hat{j} + 7 \hat{k}) \dots (i i i) \\ H e r e, \vec{a_{1}} = 8 \hat{i} - 9 \hat{j} + 10 \hat{k} a n d \vec{a_{2}} = 15 \hat{i} - 29 \hat{j} + 5 \hat{k} \\ \vec{b_{1}} = 3 \hat{i} - 16 \hat{j} + 7 \hat{k} a n d \vec{b_{2}} = 3 \hat{i} + 8 \hat{j} - 5 \hat{k} \\ \vec{a_{2}} - \vec{a_{1}} = 7 \hat{i} + 38 \hat{j} - 5 \hat{k} \\ \vec{b_{1}} \times \vec{b_{2}} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 3 & - 16 & 7 \\ 3 & 8 & - 5 \end{matrix} | \\ = \hat{i} (80 - 56) - \hat{j} (- 15 - 21) + \hat{k} (24 + 48) \\ = 24 \hat{i} + 36 \hat{j} + 72 \hat{k} \\ ∴ S h o r t e s t distance, S D = | \frac{(\vec{a_{2}} - \vec{a_{1}}) . (\vec{b_{1}} \times \vec{b_{2}})}{| \vec{b_{1}} \times \vec{b_{2}} |} | = | \frac{(7 \hat{i} + 38 \hat{j} - 5 \hat{k}) . (24 \hat{i} + 36 \hat{j} + 72 \hat{k})}{\sqrt[]{{(24)}^{2} + {(36)}^{2} + {(72)}^{2}}} | \\ = | \frac{168 + 1368 - 360}{\sqrt[]{576 + 1296 + 5184}} | = | \frac{168 + 1008}{\sqrt[]{7056}} | = \frac{1176}{84} = 14 u n i t s \\ H e n c e, t h e r e q u i r e d distance i s 14 u n i t s . \end{array}$

Find the equation of the plane which is perpendicular to the plane $5 x + 3 y + 6 z + 8 = 0$ and contains the line of intersection of the planes $x + 2 y + 3 z – 4 = 0$ and $2 x + y – z + 5 = 0$ .

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n p l a n e s a r e \\ P_{1} : 5 x + 3 y + 6 z + 8 = 0 \\ P_{2} : x + 2 y + 3 z - 4 = 0 \\ P_{3} : 2 x + y - z + 5 = 0 \\ E q u a t i o n s o f t h e p l a n e passing t h r o u g h t h e l i n e o f intersection o f P_{2} a n d P_{3} i s \\ (x + 2 y + 3 z - 4) + λ (2 x + y - z + 5) = 0 \\ \Rightarrow (1 + 2 λ) x + (2 + λ) y + (3 - λ) z - 4 + 5 λ = 0 \dots (i) \\ P l a n e (i) i s p e r p e n d i c u l a r t o P_{1}, t h e n \\ 5 (1 + 2 λ) + 3 (2 + λ) + 6 (3 - λ) = 0 \\ \Rightarrow 5 + 10 λ + 6 + 3 λ + 18 - 6 λ = 0 \\ \Rightarrow 7 λ + 29 = 0 \Rightarrow λ = \frac{- 29}{7} \\ P u t t i n g t h e v a l u e o f λ i n e q . (i), w e g e t \\ [1 + 2 (\frac{- 29}{7})] x + [2 - \frac{29}{7}] y + [3 + \frac{29}{7}] z - 4 + 5 (\frac{- 29}{7}) = 0 \\ \Rightarrow \frac{- 15}{7} x - \frac{15}{7} y + \frac{50}{7} z - 4 - \frac{145}{7} = 0 \\ \Rightarrow - 15 x - 15 y + 50 z - 28 - 145 = 0 \\ \Rightarrow - 15 x - 15 y + 50 z - 173 = 0 \Rightarrow 15 x + 15 y - 50 z + 173 = 0 \end{array}$

The plane $a x + b y = 0$ is rotated about its line of intersection with the plane $z = 0$ through an angle $α$ . Prove that the equation of the plane in its new position is $a x + b y \pm \sqrt[]{a^{2} + b^{2}} t a n (α) z = 0 .$

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n p l a n e s a r e \\ a x + b y = 0 \dots (i) \\ z = 0 \dots (i i) \\ E q u a t i o n o f a n y p l a n e passing t h r o u g h t h e l i n e o f intersection o f p l a n e (i) a n d (i i) i s \\ (a x + b y) + k z = 0 \Rightarrow a x + b y + k z = 0 \dots (i i i) \\ D i v i d i n g b o t h s i d e s b y \sqrt[]{a^{2} + b^{2} + k^{2}}, w e g e t \\ \frac{a}{\sqrt[]{a^{2} + b^{2} + k^{2}}} x + \frac{b}{\sqrt[]{a^{2} + b^{2} + k^{2}}} y + \frac{k}{\sqrt[]{a^{2} + b^{2} + k^{2}}} z = 0 \\ ∴ D i r e c t i o n cosines o f t h e n o r m a l t o t h e p l a n e a r e \\ \frac{a}{\sqrt[]{a^{2} + b^{2} + k^{2}}}, \frac{b}{\sqrt[]{a^{2} + b^{2} + k^{2}}}, \frac{k}{\sqrt[]{a^{2} + b^{2} + k^{2}}} \\ a n d t h e d i r e c t i o n cosines o f t h e p l a n e (i) a r e \\ \frac{a}{\sqrt[]{a^{2} + b^{2}}}, \frac{b}{\sqrt[]{a^{2} + b^{2}}}, 0 \\ Since, α i s t h e a n g l e b e t w e e n t h e p l a n e s (i) a n d (i i i), w e g e t \\ c o s α = \frac{a . a + b . b + k . 0}{\sqrt[]{a^{2} + b^{2} + k^{2}} . \sqrt[]{a^{2} + b^{2}}} \\ \Rightarrow c o s α = \frac{a^{2} + b^{2}}{\sqrt[]{a^{2} + b^{2} + k^{2}} . \sqrt[]{a^{2} + b^{2}}} \\ \Rightarrow c o s α = \frac{\sqrt[]{a^{2} + b^{2}}}{\sqrt[]{a^{2} + b^{2} + k^{2}}} \Rightarrow c o s^{2} α = \frac{a^{2} + b^{2}}{a^{2} + b^{2} + k^{2}} \\ \Rightarrow (a^{2} + b^{2} + k^{2}) c o s^{2} α = a^{2} + b^{2} \\ \Rightarrow a^{2} c o s^{2} α + b^{2} c o s^{2} α + k^{2} c o s^{2} α = a^{2} + b^{2} \\ \Rightarrow k^{2} c o s^{2} α = a^{2} - a^{2} c o s^{2} α + b^{2} - b^{2} c o s^{2} α \\ \Rightarrow k^{2} c o s^{2} α = a^{2} (1 - c o s^{2} α) + b^{2} (1 - c o s^{2} α) \\ \Rightarrow k^{2} c o s^{2} α = a^{2} s i n^{2} α + b^{2} s i n^{2} α \\ \Rightarrow k^{2} c o s^{2} α = (a^{2} + b^{2}) s i n^{2} α \\ \Rightarrow k^{2} = (a^{2} + b^{2}) \frac{s i n^{2} α}{c o s^{2} α} \Rightarrow k = \pm \sqrt[]{a^{2} + b^{2}} . t a n α \\ P u t t i n g t h e v a l u e o f k i n e q . (i i i) w e g e t \\ a x + b y \pm (\sqrt[]{a^{2} + b^{2}} . t a n α) z = 0 w h i c h i s t h e r e q u i r e d E q u a t i o n o f p l a n e . \\ H e n c e p r o v e d . \end{array}$

Find the equation of the plane through the intersection of the planes $\vec{r} \cdot (\hat{i} + 3 \hat{j}) - 6 = 0 and \vec{r} \cdot (3 \hat{i} - \hat{j} - 4 \hat{k}) = 0,$ whose perpendicular distance from the origin is unity.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n p l a n e s a r e : \\ \vec{r} . (\hat{i} - 3 \hat{j}) - 6 = 0 \Rightarrow x + 3 y - 6 = 0 \dots (i) \\ a n d \vec{r} . (3 \hat{i} - \hat{j} - 4 \hat{k}) = 0 \Rightarrow 3 x - y - 4 z = 0 \dots (i i) \\ E q u a t i o n o f t h e p l a n e passing t h r o u g h t h e l i n e o f intersection o f p l a n e (i) a n d (i i) i s \\ (x + 3 y - 6) + k (3 x - y - 4 z) = 0 \dots (i i i) \\ (1 + 3 k) x + (3 - k) y - 4 k z - 6 = 0 \\ P e r p e n d i c u l a r distance f r o m o r i g i n \\ \Rightarrow | \frac{- 6}{\sqrt[]{{(1 + 3 k)}^{2} + {(3 - k)}^{2} + {(- 4 k)}^{2}}} | = 1 \\ \Rightarrow \frac{36}{1 + 9 k^{2} + 6 k + 9 + k^{2} - 6 k + 16 k^{2}} = 1 [S q u a r i n g b o t h s i d e s] \\ \Rightarrow \frac{36}{26 k^{2} + 10} = 1 \Rightarrow 26 k^{2} + 10 = 36 \\ \Rightarrow 26 k^{2} = 26 \Rightarrow k^{2} = 1 ∴ k = \pm 1 \\ P u t t i n g t h e v a l u e o f k i n e q . (i i i) w e g e t, \\ (x + 3 y - 6) \pm (3 x - y - 4 z) = 0 \\ \Rightarrow x + 3 y - 6 + 3 x - y - 4 z = 0 a n d x + 3 y - 6 - 3 x + y + 4 z = 0 \\ \Rightarrow 4 x + 2 y - 4 z - 6 = 0 a n d - 2 x + 4 y + 4 z - 6 = 0 \\ H e n c e, t h e r e q u i r e d e q u a t i o n a r e \\ 4 x + 2 y - 4 z - 6 = 0 a n d - 2 x + 4 y + 4 z - 6 = 0 \end{array}$

Show that the points $(\hat{i} - \hat{j} + \hat{k})$ and 3 $(\hat{i} + \hat{j} + \hat{k})$ are equidistant from the plane and lie on opposite sides of it.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n points a r e P (\hat{i} - \hat{j} + 3 \hat{k}) a n d Q (3 \hat{i} + 3 \hat{j} + 3 \hat{k}) a n d t h e p l a n e \vec{r} . (5 \hat{i} + 2 \hat{j} - 7 \hat{k}) + 9 = 0 \\ P e r p e n d i c u l a r distance o f P (\hat{i} - \hat{j} + 3 \hat{k}) f r o m t h e p l a n e \\ \vec{r} . (5 \hat{i} + 2 \hat{j} - 7 \hat{k}) + 9 = | \frac{(\hat{i} - \hat{j} + 3 \hat{k}) . (5 \hat{i} + 2 \hat{j} - 7 \hat{k}) + 9}{\sqrt[]{{(5)}^{2} + {(2)}^{2} + {(- 7)}^{2}}} | \\ = | \frac{5 - 2 - 21 + 9}{\sqrt[]{25 + 4 + 49}} | = | \frac{- 9}{\sqrt[]{78}} | \\ a n d p e r p e n d i c u l a r distance o f Q (3 \hat{i} + 3 \hat{j} + 3 \hat{k}) f r o m t h e p l a n e \\ = | \frac{(3 \hat{i} + 3 \hat{j} + 3 \hat{k}) . (5 \hat{i} + 2 \hat{j} - 7 \hat{k}) + 9}{\sqrt[]{25 + 4 + 49}} | \\ = | \frac{15 + 6 - 21 + 9}{\sqrt[]{78}} | = | \frac{9}{\sqrt[]{78}} | \\ H e n c e, t h e t w o points a r e equidistant f r o m t h e g i v e n p l a n e . \\ O p p o s i t e s i g n s h o w s t h a t t h e y l i e o n e i t h e r s i d e o f t h e p l a n e . \end{array}$

AB = 3 $\hat{i}$ - $\hat{j}$ + $\hat{k}$ and $C D$ = -3 $\hat{i}$ + 2 $\hat{j}$ + 4 $\hat{k}$ are two vectors. The position vectors of the points A and C are 6 $\hat{i}$ + 7 $\hat{j}$ + 4 $\hat{k}$ and -9 $\hat{i}$ + 2 $\hat{j}$ + $\hat{k,}$ respectively. Find the position vector of a point P on the line AB and a point Q on the line CD such that $\vec{P Q}$ is perpendicular to both $\vec{A B}$ and $\vec{C D}$ both.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} P o s i t i o n v e c t o r o f A i s 6 \hat{i} + 7 \hat{j} + 4 \hat{k} a n d \vec{A B} = 3 \hat{i} - \hat{j} + \hat{k} \\ S o, e q u a t i o n o f a n y l i n e passing t h r o u g h A a n d p a r a l l e l t o \vec{A B} \\ \vec{r} = (6 \hat{i} + 7 \hat{j} + 4 \hat{k}) + λ (3 \hat{i} - \hat{j} + \hat{k}) \dots (i) \\ N o w a n y point P o n \vec{A B} = (6 + 3 λ, 7 - λ, 4 + λ) \\ S i m i l a r l y, p o s i t i o n v e c t o r o f C i s - 9 \hat{j} + 2 \hat{k} a n d \vec{C D} = - 3 \hat{i} + 2 \hat{j} + 4 \hat{k} \\ S o, e q u a t i o n o f a n y l i n e passing t h r o u g h C a n d p a r a l l e l t o \vec{C D} i s \\ \vec{r} = (- 9 \hat{j} + 2 \hat{k}) + μ (- 3 \hat{i} + 2 \hat{j} + 4 \hat{k}) \dots (i i) \\ A n y point Q o n \vec{C D} = (- 3 μ, - 9 + 2 μ, 2 + 4 μ) \\ d' r a t i o s o f \vec{P Q} a r e \\ (6 + 3 λ + 3 μ, 7 - λ + 9 - 2 μ, 4 + λ - 2 - 4 μ) \\ \Rightarrow (6 + 3 λ + 3 μ), (16 - λ - 2 μ), (2 + λ - 4 μ) \\ N o w \vec{P Q} i s ⊥ t o e q . (i), t h e n \\ 3 (6 + 3 λ + 3 μ) - 1 (16 - λ - 2 μ) + 1 (2 + λ - 4 μ) = 0 \\ \Rightarrow 18 + 9 λ + 9 μ - 16 + λ + 2 μ + 2 + λ - 4 μ = 0 \\ \Rightarrow 11 λ + 7 μ + 4 = 0 \dots (i i i) \\ \vec{P Q} i s ⊥ t o e q . (i i), t h e n \\ - 3 (6 + 3 λ + 3 μ) + 2 (16 - λ - 2 μ) + 4 (2 + λ - 4 μ) = 0 \\ \Rightarrow - 18 - 9 λ - 9 μ + 32 - 2 λ - 4 μ + 8 + 4 λ - 16 μ = 0 \\ \Rightarrow - 7 λ - 29 μ + 22 = 0 \\ \Rightarrow 7 λ + 29 μ - 22 = 0 \dots (i v) \\ S o l v i n g e q n . (i i i) a n d (i v) w e g e t \\ \Rightarrow 77 λ + 49 μ + 28 = 0 \\ 77 λ + 319 μ - 242 = 0 \\ \underline{(-) (-) (+)} \\ - 270 μ + 270 = 0 ∴ μ = 1 \\ P u t t i n g t h e v a l u e o f μ i n e q n . (i v) w e g e t, \\ 7 λ + 29 - 22 = 0 \Rightarrow λ = - 1 \\ ∴ P o s i t i o n v e c t o r o f P = [6 + 3 (- 1), 7 + 1, 4 - 1] = (3, 8, 3) \\ a n d P o s i t i o n v e c t o r o f Q = [- 3 (1), - 9 + 2 (1), 2 + 4 (1)] = (- 3, - 7, 6) \\ H e n c e, t h e p o s i t i o n v e c t o r o f \\ P = 3 \hat{i} + 8 \hat{j} + 3 \hat{k} a n d Q = - 3 \hat{i} - 7 \hat{j} + 6 \hat{k} \end{array}$

Show that the straight lines whose direction cosines are given by $2 l + 2 m - n = 0 and m n + n l + l m = 0$ are at right angles.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t 2 l + 2 m - n = 0 \dots (i) \\ a n d m n + n l + l m = 0 \dots (i i) \\ Eliminating m f r o m e q . (i) a n d (i i) w e g e t, \\ m = \frac{n - 2 l}{2} [F r o m (i)] \\ \Rightarrow (\frac{n - 2 l}{2}) n + n l + l (\frac{n - 2 l}{2}) = 0 \\ \Rightarrow \frac{n^{2} - 2 n l + 2 n l + n l - 2 l^{2}}{2} = 0 \\ \Rightarrow n^{2} + n l - 2 l^{2} = 0 \\ \Rightarrow n^{2} + 2 n l - n l - 2 l^{2} = 0 \\ \Rightarrow n (n + 2 l) - l (n + 2 l) = 0 \\ \Rightarrow (n - l) (n + 2 l) = 0 \\ \Rightarrow n = - 2 l a n d n = l \\ ∴ m = \frac{- 2 l - 2 l}{2}, m = \frac{l - 2 l}{2} \\ \Rightarrow m = - 2 l, m = \frac{- l}{2} \\ T h e r e f o r e, t h e d i r e c t i o n r a t i o s a r e p r o p o r t i o n a l t o l, - 2 l, - 2 l a n d l, \frac{- l}{2}, l . \\ \Rightarrow 1, - 2, - 2 a n d 2, - 1, 2 \\ I f t h e t w o l i n e s a r e p e r p e n d i c u l a r t o e a c h o t h e r t h e n \\ 1 (2) - 2 (- 1) - 2 \times 2 = 0 \\ 2 + 2 - 4 = 0 \\ 0 = 0 \\ H e n c e, t h e t w o l i n e s a r e p e r p e n d i c u l a r . \end{array}$

If $l_{1}, m_{1}, n_{1}$ ; $l_{2}, m_{2}, n_{2}$ , and $l_{3}, m_{3}, n_{3}$ are the direction cosines of three mutually perpendicular lines, prove that the line whose direction cosines are proportional to $l_{1} + l_{2} + l_{3}$ , $m_{1} + m_{2} + m_{3}$ , $n_{1} + n_{2} + n_{3}$ and makes equal angles with them.

This is a long answer type question as classified in NCERT Exemplar

$\begin{array}{l} L e t \vec{a}, \vec{b}, \vec{c} a n d \vec{d} a r e s u c h t h a t \\ \vec{a} = l_{1} \hat{i} + m_{1} \hat{j} + n_{1} \hat{k} \\ \vec{b} = l_{2} \hat{i} + m_{2} \hat{j} + n_{2} \hat{k} \\ \vec{c} = l_{3} \hat{i} + m_{3} \hat{j} + n_{3} \hat{k} \\ a n d \vec{d} = (l_{1} + l_{2} + l_{3}) \hat{i} + (m_{1} + m_{2} + m_{3}) \hat{j} + (n_{1} + n_{2} + n_{3}) \hat{k} \\ Since t h e g i v e n d' cosines a r e m u t u a l l y p e r p e n d i c u l a r t h e n \\ l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2} = 0 \\ l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3} = 0 \\ l_{1} l_{3} + m_{1} m_{3} + n_{1} n_{3} = 0 \\ L e t α, β a n d γ b e t h e a n g l e s b e t w e e n \vec{a} a n d \vec{d}, \vec{b} a n d \vec{d}, \vec{c} a n d \vec{d} r e s p e c t i v e l y . \\ ∴ c o s α = l_{1} (l_{1} + l_{2} + l_{3}) + m_{1} (m_{1} + m_{2} + m_{3}) + n_{1} (n_{1} + n_{2} + n_{3}) \\ = l_{1}^{2} + l_{1} l_{2} + l_{1} l_{3} + m_{1}^{2} + m_{1} m_{2} + m_{1} m_{3} + n_{1}^{2} + n_{1} n_{2} + n_{1} n_{3} \\ = (l_{1}^{2} + m_{1}^{2} + n_{1}^{2}) + (l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2}) + (l_{1} l_{3} + m_{1} m_{3} + n_{1} n_{3}) \\ = 1 + 0 + 0 = 1 \\ ∴ c o s β = l_{2} (l_{1} + l_{2} + l_{3}) + m_{2} (m_{1} + m_{2} + m_{3}) + n_{2} (n_{1} + n_{2} + n_{3}) \\ = l_{1} l_{2} + l_{2}^{2} + l_{2} l_{3} + m_{1} m_{2} + m_{2}^{2} + m_{2} m_{3} + n_{1} n_{2} + n_{2}^{2} + n_{2} n_{3} \\ = (l_{2}^{2} + m_{2}^{2} + n_{2}^{2}) + (l_{1} l_{2} + m_{1} m_{2} + n_{1} n_{2}) + (l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3}) \\ = 1 + 0 + 0 = 1 \\ S i m i l a r l y, \\ ∴ c o s γ = l_{3} (l_{1} + l_{2} + l_{3}) + m_{3} (m_{1} + m_{2} + m_{3}) + n_{3} (n_{1} + n_{2} + n_{3}) \\ = l_{1} l_{3} + l_{2} l_{3} + l_{3}^{2} + m_{1} m_{3} + m_{2} m_{3} + m_{3}^{2} + n_{1} n_{3} + n_{2} n_{3} + n_{3}^{2} \\ = (l_{3}^{2} + m_{3}^{2} + n_{3}^{2}) + (l_{1} l_{3} + m_{1} m_{3} + n_{1} n_{3}) + (l_{2} l_{3} + m_{2} m_{3} + n_{2} n_{3}) \\ = 1 + 0 + 0 = 1 \\ ∴ c o s α = c o s β = c o s γ = 1 \Rightarrow α = β = γ w h i c h i s t h e r e q u i r e d r e s u l t . \end{array}$

Three-Dimensional Geometry Short Answer Type Questions

1. Find the position vector of a point A in space such that $\vec{O A}$ is inclined at 60º to OX and at 45° to OY and $| \vec{O A} |$ = 10 units.

Ans.

\begin{array}{l} L e t α = 6 0^{0}, β = 4 5^{0} a n d t h e a n g l e i n c l i n e d t o O Z a x i s b e γ . \\ W e k n o w t h a t c o s^{2} α + c o s^{2} β + c o s^{2} γ = 1 \\ \Rightarrow c o s^{2} 6 0^{0} + c o s^{2} 4 5^{0} + c o s^{2} γ = 1 \\ \Rightarrow {(\frac{1}{2})}^{2} + {(\frac{1}{\sqrt[]{2}})}^{2} + c o s^{2} γ = 1 \Rightarrow \frac{1}{4} + \frac{1}{2} + c o s^{2} γ = 1 \\ \Rightarrow \frac{3}{4} + c o s^{2} γ = 1 \Rightarrow c o s^{2} γ = 1 - \frac{3}{4} = \frac{1}{4} \\ ∴ c o s γ = \pm \frac{1}{2} \Rightarrow c o s γ = \frac{1}{2} (Rejecting c o s γ = - \frac{1}{2}, since γ < 9 0^{0}) \\ ∴ \vec{O A} = | \vec{O A} | (\frac{1}{2} \hat{i} + \frac{1}{\sqrt[]{2}} \hat{j} + \frac{1}{2} \hat{k}) = 10 (\frac{1}{2} \hat{i} + \frac{1}{\sqrt[]{2}} \hat{j} + \frac{1}{2} \hat{k}) \\ = 5 \hat{i} + 5 \sqrt[]{2} \hat{j} + 5 \hat{k} \\ H e n c e, t h e p o s i t i o n v e c t o r o f A i s (5 \hat{i} + 5 \sqrt[]{2} \hat{j} + 5 \hat{k}) . \end{array}

2. Find the vector equation of the line which is parallel to the vector $3 \hat{i} - 2 \hat{j} + 6 \hat{k}$ and which passes through the point (1, –2, 3).

Ans. $\begin{array}{l} W e k n o w t h a t t h e e q u a t i o n o f l i n e i s \\ \vec{r} = \vec{a} + \vec{b} λ \\ H e r e, \vec{a} = \hat{i} - 2 \hat{j} + 3 \hat{k} a n d \vec{b} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k} \\ ∴ E q u a t i o n o f l i n e i s \vec{r} = (\hat{i} - 2 \hat{j} + 3 \hat{k}) + λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) = (\hat{i} - 2 \hat{j} + 3 \hat{k}) + λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) - (\hat{i} - 2 \hat{j} + 3 \hat{k}) = λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ \Rightarrow (x - 1) \hat{i} + (y + 2) \hat{j} + (z - 3) \hat{k} = λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s (x - 1) \hat{i} + (y + 2) \hat{j} + (z - 3) \hat{k} = λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) . \end{array}$

Commonly asked questions

Find the position vector of a point A in space such that $\vec{O A}$ is inclined at 60º to OX and at 45° to OY and $| \vec{O A} |$ = 10 units.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} L e t α = 6 0^{0}, β = 4 5^{0} a n d t h e a n g l e i n c l i n e d t o O Z a x i s b e γ . \\ W e k n o w t h a t c o s^{2} α + c o s^{2} β + c o s^{2} γ = 1 \\ \Rightarrow c o s^{2} 6 0^{0} + c o s^{2} 4 5^{0} + c o s^{2} γ = 1 \\ \Rightarrow {(\frac{1}{2})}^{2} + {(\frac{1}{\sqrt[]{2}})}^{2} + c o s^{2} γ = 1 \Rightarrow \frac{1}{4} + \frac{1}{2} + c o s^{2} γ = 1 \\ \Rightarrow \frac{3}{4} + c o s^{2} γ = 1 \Rightarrow c o s^{2} γ = 1 - \frac{3}{4} = \frac{1}{4} \\ ∴ c o s γ = \pm \frac{1}{2} \Rightarrow c o s γ = \frac{1}{2} (Rejecting c o s γ = - \frac{1}{2}, since γ < 9 0^{0}) \\ ∴ \vec{O A} = | \vec{O A} | (\frac{1}{2} \hat{i} + \frac{1}{\sqrt[]{2}} \hat{j} + \frac{1}{2} \hat{k}) = 10 (\frac{1}{2} \hat{i} + \frac{1}{\sqrt[]{2}} \hat{j} + \frac{1}{2} \hat{k}) \\ = 5 \hat{i} + 5 \sqrt[]{2} \hat{j} + 5 \hat{k} \\ H e n c e, t h e p o s i t i o n v e c t o r o f A i s (5 \hat{i} + 5 \sqrt[]{2} \hat{j} + 5 \hat{k}) . \end{array}$

Show that the lines $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4}$ and $\frac{x - 4}{5} = \frac{y - 1}{2} = z$ intersect. Also, find their point of intersection.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n e q u a t i o n s a r e \\ \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} a n d \frac{x - 4}{5} = \frac{y - 1}{2} = z \\ L e t \frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{4} = λ \\ ∴ x = 2 λ + 1, y = 3 λ + 2 a n d z = 4 λ + 3 \\ a n d \frac{x - 4}{5} = \frac{y - 1}{2} = \frac{z}{1} = μ \\ ∴ x = 5 μ + 4, y = 2 μ + 1 a n d z = μ \\ I f t h e t w o l i n e s intersect e a c h o t h e r a t o n e point, \\ t h e n 2 λ + 1 = 5 μ + 4 \Rightarrow 2 λ - 5 μ = 3 \dots (i) \\ 3 λ + 2 = 2 μ + 1 \Rightarrow 3 λ - 2 μ = - 1 \dots (i i) \\ a n d 4 λ + 3 = μ \Rightarrow 4 λ - μ = - 3 \dots (i i i) \\ S o l v i n g e q n . (i) a n d (i i) w e g e t \\ 2 λ - 5 μ = 3 (M u l t i p l y b y 3) \\ 3 λ - 2 μ = - 1 (M u l t i p l y b y 2) \\ \Rightarrow 6 λ - 15 μ = 9 \\ 6 λ - 4 μ = - 2 \\ \underline{(-) (+) (+)} \\ - 11 μ = 11 ∴ μ = - 1 \\ P u t t i n g t h e v a l u e o f μ i n e q n . (i) w e g e t, \\ 2 λ - 5 (- 1) = 3 \\ \Rightarrow 2 λ + 5 = 3 \\ \Rightarrow 2 λ = - 2 ∴ λ = - 1 \\ N o w, p u t t i n g t h e v a l u e o f λ μ i n e q n . (i i i) t h e n, \\ 4 (- 1) - (- 1) = - 3 \\ - 4 + 1 = - 3 - 3 = - 3 (s a t i s f i e d) \\ ∴ C o o r d i n a t e s o f t h e point o f intersection a r e \\ x = 5 (- 1) + 4 = - 5 + 4 = - 1 \\ y = 2 (- 1) + 1 = - 2 + 1 = - 1 \\ z = - 1 \\ H e n c e, t h e g i v e n l i n e s intersect e a c h o t h e r a t (- 1, - 1, - 1) . \end{array}$

Find the vector equation of the line which is parallel to the vector $3 \hat{i} - 2 \hat{j} + 6 \hat{k}$ and which passes through the point (1, –2, 3).

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} W e k n o w t h a t t h e e q u a t i o n o f l i n e i s \\ \vec{r} = \vec{a} + \vec{b} λ \\ H e r e, \vec{a} = \hat{i} - 2 \hat{j} + 3 \hat{k} a n d \vec{b} = 3 \hat{i} - 2 \hat{j} + 6 \hat{k} \\ ∴ E q u a t i o n o f l i n e i s \vec{r} = (\hat{i} - 2 \hat{j} + 3 \hat{k}) + λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) = (\hat{i} - 2 \hat{j} + 3 \hat{k}) + λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) - (\hat{i} - 2 \hat{j} + 3 \hat{k}) = λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ \Rightarrow (x - 1) \hat{i} + (y + 2) \hat{j} + (z - 3) \hat{k} = λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s (x - 1) \hat{i} + (y + 2) \hat{j} + (z - 3) \hat{k} = λ (3 \hat{i} - 2 \hat{j} + 6 \hat{k}) . \end{array}$

Find the angle between the lines $\vec{r} = (3 \hat{i} + 2 \hat{j} + 6 \hat{k}) + λ (2 \hat{i} + \hat{j} + 6 \hat{k})$ and $\vec{r} = (2 \hat{i} + 5 \hat{k}) + μ (6 \hat{i} + 3 \hat{j} + 2 \hat{k}) .$

$\begin{array}{l} H e r e, \vec{b_{1}} = 2 \hat{i} + \hat{j} + 2 \hat{k} a n d \vec{b_{2}} = 6 \hat{i} + 3 \hat{j} + 2 \hat{k} \\ ∴ c o s θ = \frac{\vec{b_{1}} \vec{b_{2}}}{| \vec{b_{1}} | | \vec{b_{2}} |} = \frac{(2 \hat{i} + \hat{j} + 2 \hat{k}) . (6 \hat{i} + 3 \hat{j} + 2 \hat{k})}{\sqrt[]{{(2)}^{2} + {(1)}^{2} + {(2)}^{2}} . \sqrt[]{{(6)}^{2} + {(3)}^{2} + {(2)}^{2}}} \\ = \frac{12 + 3 + 4}{\sqrt[]{4 + 1 + 4} \sqrt[]{36 + 9 + 4}} = \frac{19}{\sqrt[]{9} \sqrt[]{49}} = \frac{19}{3.7} = \frac{19}{21} \\ ∴ θ = c o s^{- 1} (\frac{19}{21}) \\ H e n c e, t h e r e q u i r e d a n g l e i s c o s^{- 1} (\frac{19}{21}) . \end{array}$

Prove that the line through A(0, –1, –1) and B(4, 5, 1) intersects the line through C(3, 9, 4) and D(–4, 4, 4).

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n points a r e A (0, - 1, - 1) a n d B (4, 5, 1) \\ C (3, 9, 4) a n d D (- 4, 4, 4) \\ C a r t e s i a n f o r m o f e q u a t i o n A B i s \\ \frac{x - 0}{4 - 0} = \frac{y + 1}{5 + 1} = \frac{z + 1}{1 + 1} \Rightarrow \frac{x}{4} = \frac{y + 1}{6} = \frac{z + 1}{2} \\ a n d i t s v e c t o r f o r m i s \vec{r} = (- \hat{j} - \hat{k}) + λ (4 \hat{i} + 6 \hat{j} + 2 \hat{k}) \\ S i m i l a r l y, e q u a t i o n o f C D i s \\ \frac{x - 3}{- 4 - 3} = \frac{y - 9}{4 - 9} = \frac{z - 4}{4 - 4} \Rightarrow \frac{x - 3}{- 7} = \frac{y - 9}{- 5} = \frac{z - 4}{0} \\ a n d i t s v e c t o r f o r m i s \vec{r} = (3 \hat{i} + 9 \hat{j} + 4 \hat{k}) + μ (- 7 \hat{i} - 5 \hat{j}) \\ N o w, h e r e \vec{a_{1}} = - \hat{j} - \hat{k}, \vec{b_{1}} = 4 \hat{i} + 6 \hat{j} + 2 \hat{k} \\ a n d \vec{a_{2}} = 3 \hat{i} + 9 \hat{j} + 4 \hat{k}, \vec{b_{2}} = - 7 \hat{i} - 5 \hat{j} \\ S h o r t e s t distance b e t w e e n A B a n d C D \\ S . D . = | \frac{(\vec{a_{2}} - \vec{a_{1}}) (\vec{b_{1}} \times \vec{b_{2}})}{| \vec{b_{1}} \times \vec{b_{2}} |} | \\ \vec{a_{2}} - \vec{a_{1}} = (3 \hat{i} + 9 \hat{j} + 4 \hat{k}) - (- \hat{j} - \hat{k}) = 3 \hat{i} + 10 \hat{j} + 5 \hat{k} \\ \vec{b_{1}} \times \vec{b_{2}} = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 4 & 6 & 2 \\ - 7 & - 5 & 0 \end{matrix} | \\ = \hat{i} (0 + 10) - \hat{j} (0 + 14) + \hat{k} (- 20 + 42) \\ = 10 \hat{i} - 14 \hat{j} + 22 \hat{k} \\ | \vec{b_{1}} \times \vec{b_{2}} | = \sqrt[]{{(10)}^{2} + {(- 14)}^{2} + {(22)}^{2}} = \sqrt[]{100 + 196 + 484} = \sqrt[]{780} \\ ∴ S . D = \frac{(3 \hat{i} + 10 \hat{j} + 5 \hat{k}) . (10 \hat{i} - 14 \hat{j} + 22 \hat{k})}{\sqrt[]{780}} = \frac{30 - 140 + 110}{\sqrt[]{780}} = 0 \\ H e n c e, t h e t w o l i n e s intersect e a c h o t h e r . \end{array}$

Prove that the lines $x = p y + q, z = r y + s$ and $x = p ’ y + q ’, z = r ’ y + s ’$ are perpendicular if $p p ’ + r r ’ + 1 = 0$

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t : x = p y + q \Rightarrow y = \frac{x - q}{p} \\ a n d z = r y + s \Rightarrow y = \frac{z - s}{r} \\ ∴ t h e e q u a t i o n b e c o m e s \\ \frac{x - q}{p} = \frac{y}{1} = \frac{z - s}{r} i n w h i c h d^{'} r a t i o s a r e a_{1} = p, b_{1} = 1, c_{1} = r \\ S i m i l a r l y x = p^{'} y + q^{'} \Rightarrow y = \frac{x - q^{'}}{p^{'}} \\ a n d z = r^{'} y + s^{'} \Rightarrow y = \frac{z - s^{'}}{r^{'}} \\ ∴ t h e e q u a t i o n b e c o m e s \\ \frac{x - q^{'}}{p^{'}} = \frac{y}{1} = \frac{z - s^{'}}{r^{'}} i n w h i c h a_{2} = p^{'}, b_{2} = 1, c_{2} = r^{'} \\ I f t h e l i n e s a r e p e r p e n d i c u l a r t o e a c h o t h e r, t h e n \\ a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2} = 0 \\ p p^{'} + 1.1 + r r^{'} = 0 \\ H e n c e, t h e r e q u i r e d c o n d i t i o n i s p p^{'} + 1.1 + r r^{'} = 0 \end{array}$

Find the equation of a plane which bisects perpendicularly the line joining the points A(2, 3, 4) and B(4, 5, 8) at right angles.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n t h a t A (2, 3, 4) a n d B (4, 5, 8) \\ C o o r d i n a t e s o f m i d - point C a r e (\frac{2 + 4}{2}, \frac{3 + 5}{2}, \frac{4 + 8}{2}) = (3, 4, 6) \\ N o w d i r e c t i o n r a t i o s o f t h e n o r m a l t o t h e p l a n e = d i r e c t i o n r a t i o s o f A B \\ = 4 - 2, 5 - 3, 8 - 4 = (2, 2, 4) \\ E q u a t i o n o f t h e p l a n e i s \\ a (x - x_{1}) + b (y - y_{1}) + c (z - z_{1}) = 0 \\ \Rightarrow 2 (x - 3) + 2 (y - 4) + 4 (z - 6) = 0 \\ \Rightarrow 2 x - 6 + 2 y - 8 + 4 z - 24 = 0 \\ \Rightarrow 2 x + 2 y + 4 z = 38 \\ \Rightarrow x + y + 2 z = 19 \\ H e n c e, t h e r e q u i r e d e q u a t i o n o f p l a n e i s \\ x + y + 2 z = 19 o r \vec{r} (\hat{i} + \hat{j} + 2 \hat{k}) = 19 . \end{array}$

Find the equation of a plane which is at a distance of $3 \sqrt[]{3}$ units from the origin and the normal to which is equally inclined to coordinate axes.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} Since, t h e n o r m a l t o t h e p l a n e i s e q u a l l y i n c l i n e d t o t h e a x i s \\ ∴ c o s α = c o s β = c o s γ \\ \Rightarrow c o s^{2} α + c o s^{2} α + c o s^{2} α = 1 \\ \Rightarrow 3 c o s^{2} α = 1 \Rightarrow c o s α = \frac{1}{\sqrt[]{3}} \\ \Rightarrow c o s α = c o s β = c o s γ = \frac{1}{\sqrt[]{3}} \\ S o, t h e n o r m a l i s \vec{N} = \frac{1}{\sqrt[]{3}} \hat{i} + \frac{1}{\sqrt[]{3}} \hat{j} + \frac{1}{\sqrt[]{3}} \hat{k} \\ ∴ E q u a t i o n o f t h e p l a n e i s \vec{r} . \vec{N} = d \\ \Rightarrow \vec{r} . \frac{\vec{N}}{| \vec{N} |} = d \\ \Rightarrow \frac{\vec{r} . (\frac{1}{\sqrt[]{3}} \hat{i} + \frac{1}{\sqrt[]{3}} \hat{j} + \frac{1}{\sqrt[]{3}} \hat{k})}{1} = 3 \sqrt[]{3} \\ \Rightarrow \vec{r} . (\frac{1}{\sqrt[]{3}} \hat{i} + \frac{1}{\sqrt[]{3}} \hat{j} + \frac{1}{\sqrt[]{3}} \hat{k}) = 3 \sqrt[]{3} \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) . \frac{1}{\sqrt[]{3}} (\hat{i} + \hat{j} + \hat{k}) = 3 \sqrt[]{3} \\ \Rightarrow x + y + z = 3 \sqrt[]{3} . \sqrt[]{3} = 9 \\ H e n c e, t h e r e q u i r e d e q u a t i o n o f p l a n e i s x + y + z = 9 . \end{array}$

If the line drawn from the point (–2, –1, –3) meets a plane at right angles at the point (1, –3, 3), find the equation of the plane.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} D i r e c t i o n r a t i o s o f t h e n o r m a l t o t h e p l a n e a r e \\ = (1 + 2, - 3 + 1, 3 + 3) = (3, - 2, 6) \\ E q u a t i o n o f t h e p l a n e passing t h r o u g h o n e point (x_{1}, y_{1}, z_{1}) i s \\ a (x - x_{1}) + b (y - y_{1}) + c (z - z_{1}) = 0 \\ \Rightarrow 3 (x - 1) - 2 (y + 3) + 6 (z - 3) = 0 \\ \Rightarrow 3 x - 3 - 2 y - 6 + 6 z - 18 = 0 \\ \Rightarrow 3 x - 2 y + 6 z = 27 \\ H e n c e, t h e r e q u i r e d e q u a t i o n o f p l a n e i s 3 x - 2 y + 6 z = 27 \end{array}$

Find the equation of the plane through the points (2, 1, 0), (3, –2, –2), and (3, 1, 7).

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} Since, t h e e q u a t i o n o f t h e p l a n e passing t h r o u g h t h e p o i n t s (x_{1}, y_{1}, z_{1}), (x_{2}, y_{2}, z_{2}) a n d (x_{3}, y_{3}, z_{3}) i s \\ \Rightarrow | \begin{matrix} x - x_{1} & y - y_{1} & z - z_{1} \\ x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \\ x_{3} - x_{1} & y_{3} - y_{1} & z_{3} - z_{1} \end{matrix} | = 0 \\ \Rightarrow | \begin{matrix} x - 2 & y - 1 & z - 0 \\ 3 - 2 & - 2 - 1 & - 2 - 0 \\ 3 - 2 & 1 - 1 & 7 - 0 \end{matrix} | = 0 \\ \Rightarrow | \begin{matrix} x - 2 & y - 1 & z \\ 1 & - 3 & - 2 \\ 1 & 0 & 7 \end{matrix} | = 0 \\ \Rightarrow (x - 2) | \begin{matrix} - 3 & - 2 \\ 0 & 7 \end{matrix} | - (y - 1) | \begin{matrix} 1 & - 2 \\ 1 & 7 \end{matrix} | + z | \begin{matrix} 1 & - 3 \\ 1 & 0 \end{matrix} | = 0 \\ \Rightarrow (x - 2) (- 21) - (y - 1) (7 + 2) + z (3) = 0 \\ \Rightarrow - 21 (x - 2) - 9 (y - 1) + 3 z = 0 \\ \Rightarrow - 21 x + 42 - 9 y + 9 + 3 z = 0 \\ \Rightarrow - 21 x - 9 y + 3 z + 51 = 0 \Rightarrow 7 x + 3 y - z - 17 = 0 \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s 7 x + 3 y - z - 17 = 0 \end{array}$

Find the equations of the two lines through the origin which intersect the line $\frac{x - 3}{2} = \frac{y - 1}{1} = \frac{z}{1}$ at angles of $\frac{π}{3}$ each.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} A n y point o n t h e g i v e n l i n e i s \\ \frac{x - 3}{2} = \frac{y - 3}{1} = \frac{z}{1} = λ \\ \Rightarrow x = 2 λ + 3, y = λ + 3 a n d z = λ \\ L e t i t b e t h e c o o r d i n a t e s o f P \\ ∴ D i r e c t i o n r a t i o s o f O P a r e (2 λ + 3 - 0), (λ + 3 - 0) a n d (λ - 0) \\ \Rightarrow 2 λ + 3, λ + 3, λ \\ B u t t h e d i r e c t i o n s r a t i o s o f t h e l i n e P Q a r e 2, 1, 1 \\ ∴ c o s θ = \frac{a_{1} a_{2} + b_{1} b_{2} + c_{1} c_{2}}{\sqrt[]{a_{1}^{2} + b_{1}^{2} + c_{1}^{2}} \sqrt[]{a_{2}^{2} + b_{2}^{2} + c_{2}^{2}}} \\ \Rightarrow c o s \frac{π}{3} = \frac{2 (2 λ + 3) + 1 (λ + 3) + 1 . λ}{\sqrt[]{{(2)}^{2} + {(1)}^{2} + {(1)}^{2}} . \sqrt[]{{(2 λ + 3)}^{2} + {(λ + 3)}^{2} + {(λ)}^{2}}} \\ \Rightarrow \frac{1}{2} = \frac{4 λ + 6 + λ + 3 + λ}{\sqrt[]{4 λ^{2} + 9 + 12 λ + λ^{2} + 9 + 6 λ + λ^{2}}} \\ \Rightarrow \frac{\sqrt[]{6}}{2} = \frac{6 λ + 9}{\sqrt[]{6 λ^{2} + 18 λ + 18}} = \frac{6 λ + 9}{\sqrt[]{6} \sqrt[]{λ^{2} + 3 λ + 3}} \\ \Rightarrow \frac{6}{2} = \frac{3 (2 λ + 3)}{\sqrt[]{λ^{2} + 3 λ + 3}} \Rightarrow 3 = \frac{3 (2 λ + 3)}{\sqrt[]{λ^{2} + 3 λ + 3}} \\ \Rightarrow 1 = \frac{2 λ + 3}{\sqrt[]{λ^{2} + 3 λ + 3}} \Rightarrow \sqrt[]{λ^{2} + 3 λ + 3} = 2 λ + 3 \\ \Rightarrow λ^{2} + 3 λ + 3 = 4 λ^{2} + 12 λ + 9 (S q u a r i n g b o t h s i d e s) \\ \Rightarrow 3 λ^{2} + 9 λ + 6 = 0 \Rightarrow λ^{2} + 3 λ + 2 = 0 \\ \Rightarrow (λ + 1) (λ + 2) = 0 ∴ λ = - 1, λ = - 2 \\ ∴ D i r e c t i o n s r a t i o s a r e [2 (- 1) + 3, - 1 + 3, - 1] i . e ., 1, 2, - 1 w h e n λ = - 1 a n d \\ [2 (- 2) + 3, - 2 + 3, - 2] i . e ., - 1, 1, - 2 w h e n λ = - 2 . \\ H e n c e, t h e r e q u i r e d e q u a t i o n s a r e \frac{x}{1} = \frac{y}{2} = \frac{z}{- 1} a n d \frac{x}{- 1} = \frac{y}{1} = \frac{z}{- 2} \end{array}$

Find the angle between the lines whose direction cosines are given by the equations $l + m + n = 0, l^{2} + m^{2} - n^{2} = 0 .$

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n e q u a t i o n s a r e \\ l + m + n = 0 \dots (i) \\ l^{2} + m^{2} + n^{2} = 0 \dots (i i) \\ F r o m e q u a t i o n (i) n = - (l + m) \\ P u t t i n g t h e v a l u e o f n i n e q . (i i) w e g e t \\ l^{2} + m^{2} + [- {(l + m)}^{2}] = 0 \\ \Rightarrow l^{2} + m^{2} - l^{2} - m^{2} - 2 l m = 0 \\ \Rightarrow - 2 l m = 0 \\ \Rightarrow l m = 0 \Rightarrow (- m - n) m = 0 [? l = - m - n] \\ \Rightarrow (m + n) m = 0 \Rightarrow m = 0 o r m = - n \\ \Rightarrow l = 0 o r l = - n \\ ∴ D i r e c t i o n c o s i n e s o f t h e t w o l i n e s a r e \\ 0, - n, n a n d - n, 0, n \Rightarrow 0, - 1, 1 a n d - 1, 0, 1 \\ ∴ c o s θ = \frac{(0 \hat{i} - \hat{j} + \hat{k}) . (- \hat{i} + 0 \hat{j} + \hat{k})}{\sqrt[]{{(- 1)}^{2} + {(1)}^{2}} \sqrt[]{{(- 1)}^{2} + {(1)}^{2}}} = \frac{1}{\sqrt[]{2} . \sqrt[]{2}} = \frac{1}{2} \\ ∴ θ = \frac{π}{3} \\ H e n c e, t h e r e q u i r e d a n g l e i s \frac{π}{3} . \end{array}$

If a variable line in two adjacent positions has direction cosines $l, m, n$ and $l + δ l, m + δ m, n + δ n$ ,show that the small angle $δ θ$ between the two positions is given by $δ θ^{2} = δ l^{2} + δ m^{2} + δ n^{2} .$

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n t h a t l, m, n a n d l + δ l, m + δ m, n + δ n a r e t h e d i r e c t i o n c o s i n e s o f a variable \\ l i n e i n t w o p o s i t i o n s \\ ∴ l^{2} + m^{2} + n^{2} = 1 \dots (i) \\ a n d {(l + δ l)}^{2} + {(m + δ m)}^{2} + {(n + δ n)}^{2} = 1 \dots (i i) \\ \Rightarrow l^{2} + δ l^{2} + 2 l . δ l + m^{2} + δ m^{2} + 2 m . δ m + n^{2} + δ n^{2} + 2 n . δ n = 1 \\ \Rightarrow (l^{2} + m^{2} + n^{2}) + (δ l^{2} + δ m^{2} + δ n^{2}) + 2 (l . δ l + m . δ m + n . δ n) = 1 \\ \Rightarrow 1 + (δ l^{2} + δ m^{2} + δ n^{2}) + 2 (l . δ l + m . δ m + n . δ n) = 1 \\ \Rightarrow l . δ l + m . δ m + n . δ n = - \frac{1}{2} (δ l^{2} + δ m^{2} + δ n^{2}) \\ L e t \vec{a} a n d \vec{b} b e t h e u n i t v e c t o r s a l o n g a l i n e w i t h d^{'} c o s i n e s l, m, n a n d (l + δ l), (m + δ m), (n + δ n) \\ ∴ \vec{a} = l \hat{i} + m \hat{j} + n \hat{k} a n d \vec{b} = (l + δ l) \hat{i} + (m + δ m) \hat{j} + (n + δ n) \hat{k} \\ ∴ c o s δ θ = \frac{\vec{a} . \vec{b}}{| \vec{a} | . | \vec{b} |} \\ \Rightarrow c o s δ θ = \frac{(l \hat{i} + m \hat{j} + n \hat{k}) [(l + δ l) \hat{i} + (m + δ m) \hat{j} + (n + δ n) \hat{k}]}{1.1} [? | \vec{a} | = | \vec{b} | = 1] \\ \Rightarrow c o s δ θ = l (l + δ l) + m (m + δ m) + n (n + δ n) \\ \Rightarrow c o s δ θ = l^{2} + l . δ l + m^{2} + m . δ m + n^{2} + n . δ n \\ \Rightarrow c o s δ θ = (l^{2} + m^{2} + n^{2}) + (l . δ l + m . δ m + n . δ n) \\ \Rightarrow c o s δ θ = 1 - \frac{1}{2} (δ l^{2} + δ m^{2} + δ n^{2}) \\ \Rightarrow 1 - c o s δ θ = \frac{1}{2} (δ l^{2} + δ m^{2} + δ n^{2}) \\ \Rightarrow 2 s i n^{2} \frac{δ θ}{2} = \frac{1}{2} (δ l^{2} + δ m^{2} + δ n^{2}) \\ \Rightarrow 4 s i n^{2} \frac{δ θ}{2} = δ l^{2} + δ m^{2} + δ n^{2} \\ \Rightarrow 4 {(\frac{δ θ}{2})}^{2} = δ l^{2} + δ m^{2} + δ n^{2} [? \frac{δ θ}{2} i s v e r y s m a l l s o, s i n \frac{δ θ}{2} = \frac{δ θ}{2}] \\ \Rightarrow {(δ θ)}^{2} = δ l^{2} + δ m^{2} + δ n^{2} H e n c e p r o v e d . \end{array}$

O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of the plane through A at right angles to OA.

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} W e h a v e A (a, b, c) a n d O (0, 0, 0) \\ ∴ d i r e c t i o n r a t i o s o f O A = a - 0, b - 0, c - 0 \\ ∴ d i r e c t i o n c o s i n e s o f l i n e O A = \frac{a}{\sqrt[]{a^{2} + b^{2} + c^{2}}}, \frac{b}{\sqrt[]{a^{2} + b^{2} + c^{2}}}, \frac{c}{\sqrt[]{a^{2} + b^{2} + c^{2}}} \\ N o w, d i r e c t i o n r a t i o s o f t h e n o r m a l t o t h e p l a n e a r e (a, b, c) . \\ ∴ E q u a t i o n o f t h e p l a n e passing t h r o u g h t h e point A (a, b, c) i s \\ a (x - a) + b (y - b) + c (z - c) = 0 \\ \Rightarrow a x - a^{2} + b y - b^{2} + c z - c^{2} = 0 \\ \Rightarrow a x + b y + c z = a^{2} + b^{2} + c^{2} \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s a x + b y + c z = a^{2} + b^{2} + c^{2} . \end{array}$

Two systems of rectangular axes have the same origin. If a plane cuts them at distances a, b, c and a′, b′, c′, respectively, from the origin, prove that $\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} = \frac{1}{a ’^{2}} + \frac{1}{b ’^{2}} + \frac{1}{c ’^{2}} .$

This is a short answer type question as classified in NCERT Exemplar

$\begin{array}{l} L e t O X, O Y, O Z a n d o x, o y, o z b e t w o rectangular s y s t e m s \\ ∴ E q u a t i o n s o f t w o p l a n e s a r e \\ \frac{X}{a}, \frac{Y}{b}, \frac{Z}{c} = 1 \dots (i) a n d \frac{x}{a^{'}}, \frac{y}{b^{'}}, \frac{z}{c^{'}} = 1 \dots (i i) \\ L e n g t h o f p e r p e n d i c u l a r f r o m o r i g i n t o p l a n e (i) i s \\ = \frac{\frac{0}{a} + \frac{0}{b} + \frac{0}{c} - 1}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} = \frac{1}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} \\ L e n g t h o f p e r p e n d i c u l a r f r o m o r i g i n t o p l a n e (i i) i s \\ = \frac{\frac{0}{a^{'}} + \frac{0}{b^{'}} + \frac{0}{c^{'}} - 1}{\sqrt[]{\frac{1}{{a^{'}}^{2}} + \frac{1}{{b^{'}}^{2}} + \frac{1}{{c^{'}}^{2}}}} = \frac{1}{\sqrt[]{\frac{1}{{a^{'}}^{2}} + \frac{1}{{b^{'}}^{2}} + \frac{1}{{c^{'}}^{2}}}} \\ A s p e r t h e c o n d i t i o n o f t h e q u e s t i o n \\ \frac{1}{\sqrt[]{\frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}}}} = \frac{1}{\sqrt[]{\frac{1}{{a^{'}}^{2}} + \frac{1}{{b^{'}}^{2}} + \frac{1}{{c^{'}}^{2}}}} \\ H e n c e, \frac{1}{a^{2}} + \frac{1}{b^{2}} + \frac{1}{c^{2}} = \frac{1}{{a^{'}}^{2}} + \frac{1}{{b^{'}}^{2}} + \frac{1}{{c^{'}}^{2}} \end{array}$

Three-Dimensional Geometry Objective Type Questions

1. The distance of the point $(α, β, γ)$ from the y-axis is

(A) $β$

(B) $γ$

(C) $\sqrt[]{β^{2} + γ^{2}}$

(D) $α^{2} + γ^{2}$

Ans. $\begin{array}{l} T h e g i v e n point i s (α, β, γ) \\ A n y point o n y - a x i s = (0, β, 0) \\ ∴ Required distance = \sqrt[]{{(α - 0)}^{2} + {(β - β)}^{2} + {(δ - 0)}^{2}} \\ = \sqrt[]{α^{2} + γ^{2}} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

2. If the direction cosines of a line are $k, k, k$ , then:

(A) $k > 0$

(B) $0 < k < 1$

(C) $k = 1$

(D) $k = \frac{1}{\sqrt[]{3}}$ or - $\frac{1}{\sqrt[]{3}}$

Ans. $\begin{array}{l} I f l, m, n a r e t h e d i r e c t i o n c o s i n e s o f a l i n e, t h e n \\ l^{2} + m^{2} + n^{2} = 1 \\ S o, k^{2} + k^{2} + k^{2} = 1 \\ \Rightarrow 3 k^{2} = 1 \Rightarrow k = \pm \frac{1}{\sqrt[]{3}} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

Commonly asked questions

The distance of the point $(α, β, γ)$ from the y-axis is

(A) $β$

(B) $γ$

(C) $\sqrt[]{β^{2} + γ^{2}}$

(D) $α^{2} + γ^{2}$

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n point i s (α, β, γ) \\ A n y point o n y - a x i s = (0, β, 0) \\ ∴ Required distance = \sqrt[]{{(α - 0)}^{2} + {(β - β)}^{2} + {(δ - 0)}^{2}} \\ = \sqrt[]{α^{2} + γ^{2}} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

If the direction cosines of a line are $k, k, k$ , then:

(A) $k > 0$

(B) $0 < k < 1$

(C) $k = 1$

(D) $k = \frac{1}{\sqrt[]{3}}$ or - $\frac{1}{\sqrt[]{3}}$

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} I f l, m, n a r e t h e d i r e c t i o n c o s i n e s o f a l i n e, t h e n \\ l^{2} + m^{2} + n^{2} = 1 \\ S o, k^{2} + k^{2} + k^{2} = 1 \\ \Rightarrow 3 k^{2} = 1 \Rightarrow k = \pm \frac{1}{\sqrt[]{3}} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The distance of the plane from the origin is:

(A) 1

(B) 7

(C) $\frac{1}{7}$

(D) None of these

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t \vec{r} . (\frac{2}{7} \hat{i} + \frac{3}{7} \hat{j} - \frac{6}{7} \hat{k}) = 1 \\ S o, t h e distance o f t h e g i v e n p l a n e f r o m t h e o r i g i n i s \\ = | \frac{- 1}{\sqrt[]{{(\frac{2}{7})}^{2} + {(\frac{3}{7})}^{2} + {(\frac{- 6}{7})}^{2}}} | = | \frac{- 1}{\sqrt[]{\frac{4}{49} + \frac{9}{49} + \frac{36}{49}}} | = \frac{1}{1} = 1 \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The sine of the angle between the straight line $\frac{x - 2}{3} = \frac{y - 4}{4} = \frac{z - 5}{5}$ and the plane $2 x - 2 y + z = 5$ is:

(A) $\frac{10}{6 \sqrt[]{5}}$

(B) $\frac{4}{5 \sqrt[]{2}}$

(C) $\frac{2}{3 \sqrt[]{5}}$

(D) $\frac{\sqrt 2}{10}$

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t l : \frac{x - 2}{3} = \frac{y - 3}{4} = \frac{z - 4}{5} \\ a n d P : 2 x - 2 y + z = 5 \\ d' r a t i o s o f t h e l i n e a r e 3, 4, 5 \\ a n d d' r a t i o s o f t h e n o r m a l t o t h e p l a n e a r e 2, - 2, 1 \\ ∴ s i n θ = \frac{3 (2) + 4 (- 2) + 5 (1)}{\sqrt[]{9 + 16 + 25} . \sqrt[]{4 + 4 + 1}} \\ \Rightarrow s i n θ = \frac{6 - 8 + 5}{\sqrt[]{50} . 3} = \frac{3}{5 \sqrt[]{2}} = \frac{\sqrt[]{2}}{10} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The reflection of the point $(α, β, γ)$ in the xy-plane is

(A) $(α, β, 0)$

(B) $(0, 0, γ)$

(C) $(- α, - β, γ)$

(D) $(α, β, - γ)$

This is a Objective Type Questions as classified in NCERT Exemplar

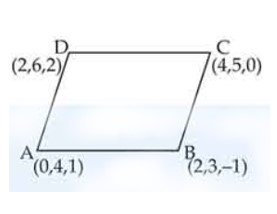
$\begin{array}{l} Reflextion o f point (α, β, γ) i n x y - p l a n e i s (α, β, - γ) \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The area of the quadrilateral ABCD, where A(0, 4, 1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to:

(A) 9 sq. units

(B) 18 sq. units

(C) 27 sq. units

(D) 81 sq. units

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n points a r e A (0, 4, 1), B (2, 3, - 1), C (4, 5, 0) a n d D (2, 6, 2) \\ d' r a t i o s o f A B = 2, - 1, - 2 \\ a n d d' r a t i o s o f D C = 2, - 1, - 2 \\ ∴ A B ? D C \\ S o, ? A B C D i s a parallelogram . \\ \vec{A B} = 2 \hat{i} - \hat{j} + 2 \hat{k} a n d \vec{A D} = 2 \hat{i} + 2 \hat{j} + \hat{k} \\ ∴ A r e a o f parallelogram A B C D = | \vec{A B} \times \vec{A D} | \\ = | \begin{matrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & - 1 & - 2 \\ 2 & 2 & 1 \end{matrix} | \\ = \hat{i} (- 1 + 4) - \hat{j} (2 + 4) + \hat{k} (4 + 2) = 3 \hat{i} - 6 \hat{j} + 6 \hat{k} \\ = \sqrt[]{{(3)}^{2} + {(- 6)}^{2} + {(6)}^{2}} = \sqrt[]{9 + 36 + 36} = \sqrt[]{81} = 9 S q u n i t s \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The locus represented by $x y + y z = 0$ is:

(A) A pair of perpendicular lines

(B) A pair of parallel lines

(C) A pair of parallel planes

(D) A pair of perpendicular planes

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n t h a t x y + y z = 0 \\ y . (x + z) = 0 \\ y = 0 o r x + z = 0 \\ H e r e, y = 0 i s o n e p l a n e a n d x + z = 0 i s a n o t h e r p l a n e . S o, i t i s a p a i r o f p e r p e n d i c u l a r p l a n e s . \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The plane $2 x - 3 y + 6 z - 11 = 0$ makes an angle $s i n^{- 1} (α)$ with the x-axis. The value of $α$ is equal to:

(A) $\frac{\sqrt[]{3}}{2}$

(B) $\frac{\sqrt[]{2}}{3}$

(C) $\frac{2}{7}$

(D) $\frac{3}{7}$

This is a Objective Type Questions as classified in NCERT Exemplar

$\begin{array}{l} D i r e c t i o n r a t i o s o f t h e n o r m a l t o t h e p l a n e 2 x - 3 y + 6 z - 11 = 0 a r e 2, - 3, 6 \\ D i r e c t i o n r a t i o s o f x - a x i s a r e 1, 0, 0 \\ ∴ a n g l e b e t w e e n p l a n e a n d t h e l i n e i s \\ ∴ s i n θ = \frac{2 (1) - 3 (0) + 6 (0)}{\sqrt[]{{(2)}^{2} + {(- 3)}^{2} + {(6)}^{2}} . \sqrt[]{{(1)}^{2} + {(0)}^{2} + {(0)}^{2}}} \\ \Rightarrow s i n θ = \frac{2}{\sqrt[]{4 + 9 + 36}} = \frac{2}{7} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Three-Dimensional Geometry Fill in the blanks Type Questions

1. A plane passes through the points (2, 0, 0), (0, 3, 0), and (0, 0, 4). The equation of the plane is __________.

Ans. $\begin{array}{l} G i v e n points a r e (2, 0, 0), (0, 3, 0) a n d (0, 0, 4) . \\ S o, t h e intercepts c u t s b y t h e p l a n e o n t h e a x e s a r e 2, 3, 4 \\ E q u a t i o n o f t h e p l a n e (intercept f o r m) i s \\ \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 \Rightarrow \frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1 \\ H e n c e, t h e e q u a t i o n o f t h e p l a n e i s \frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1 \end{array}$

2. The direction cosines of the vector $(2 \hat{i} + 2 \hat{j} - \hat{k})$ are __________.

Ans. $\begin{array}{l} L e t \vec{a} = 2 \hat{i} + 2 \hat{j} - \hat{k} \\ d i r e c t i o n r a t i o s o f \vec{a} a r e 2, 2, - 1 \\ ∴ t h e d i r e c t i o n cosines a r e \frac{2}{\sqrt[]{4 + 4 + 1}}, \frac{2}{\sqrt[]{4 + 4 + 1}}, \frac{- 1}{\sqrt[]{4 + 4 + 1}} \\ \Rightarrow \frac{2}{3}, \frac{2}{3}, \frac{- 1}{3} \\ H e n c e, t h e d i r e c t i o n cosines o f t h e g i v e n v e c t o r a r e \frac{2}{3}, \frac{2}{3}, \frac{- 1}{3} . \end{array}$

Commonly asked questions

A plane passes through the points (2, 0, 0), (0, 3, 0), and (0, 0, 4). The equation of the plane is __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n points a r e (2, 0, 0), (0, 3, 0) a n d (0, 0, 4) . \\ S o, t h e intercepts c u t s b y t h e p l a n e o n t h e a x e s a r e 2, 3, 4 \\ E q u a t i o n o f t h e p l a n e (intercept f o r m) i s \\ \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1 \Rightarrow \frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1 \\ H e n c e, t h e e q u a t i o n o f t h e p l a n e i s \frac{x}{2} + \frac{y}{3} + \frac{z}{4} = 1 \end{array}$

The direction cosines of the vector $(2 \hat{i} + 2 \hat{j} - \hat{k})$ are __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} L e t \vec{a} = 2 \hat{i} + 2 \hat{j} - \hat{k} \\ d i r e c t i o n r a t i o s o f \vec{a} a r e 2, 2, - 1 \\ ∴ t h e d i r e c t i o n cosines a r e \frac{2}{\sqrt[]{4 + 4 + 1}}, \frac{2}{\sqrt[]{4 + 4 + 1}}, \frac{- 1}{\sqrt[]{4 + 4 + 1}} \\ \Rightarrow \frac{2}{3}, \frac{2}{3}, \frac{- 1}{3} \\ H e n c e, t h e d i r e c t i o n cosines o f t h e g i v e n v e c t o r a r e \frac{2}{3}, \frac{2}{3}, \frac{- 1}{3} . \end{array}$

The vector equation of the line $\frac{x - 5}{3} = \frac{y + 4}{7} = \frac{z - 6}{2}$ is __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n e q u a t i o n i s \\ \frac{x - 5}{3} = \frac{y + 4}{7} = \frac{z - 6}{2} \\ H e r e, \vec{a} = (5 \hat{i} - 4 \hat{j} + 6 \hat{k}) a n d \vec{b} = (3 \hat{i} + 7 \hat{j} + 2 \hat{k}) \\ E q u a t i o n o f t h e l i n e i s \vec{r} = \vec{a} + \vec{b} λ \\ H e n c e, t h e v e c t o r e q u a t i o n o f t h e g i v e n l i n e i s \\ \vec{r} = (5 \hat{i} - 4 \hat{j} + 6 \hat{k}) + λ (3 \hat{i} + 7 \hat{j} + 2 \hat{k}) \end{array}$

The vector equation of the line through the points (3, 4, –7) and (1, –1, 6) is __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n points a r e (3, 4, - 7) a n d (1, - 1, 6) \\ H e r e, \vec{a} = 3 \hat{i} + 4 \hat{j} - 7 \hat{k} a n d \vec{b} = \hat{i} - \hat{j} + 6 \hat{k} \\ E q u a t i o n o f t h e l i n e i s \vec{r} = \vec{a} + λ (\vec{b} - \vec{a}) \\ \Rightarrow \vec{r} = (3 \hat{i} + 4 \hat{j} - 7 \hat{k}) + λ [(\hat{i} - \hat{j} + 6 \hat{k}) - (3 \hat{i} + 4 \hat{j} - 7 \hat{k})] \\ \Rightarrow \vec{r} = (3 \hat{i} + 4 \hat{j} - 7 \hat{k}) + λ (- 2 \hat{i} + - 5 \hat{j} + 13 \hat{k}) \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) = (3 \hat{i} + 4 \hat{j} - 7 \hat{k}) + λ (- 2 \hat{i} + - 5 \hat{j} + 13 \hat{k}) \\ \Rightarrow (x - 3) \hat{i} + (y - 4) \hat{j} + (z + 7) \hat{k} = λ (- 2 \hat{i} + - 5 \hat{j} + 13 \hat{k}) \\ H e n c e, t h e v e c t o r e q u a t i o n o f t h e l i n e i s \\ (x - 3) \hat{i} + (y - 4) \hat{j} + (z + 7) \hat{k} = λ (- 2 \hat{i} + - 5 \hat{j} + 13 \hat{k}) \end{array}$

The cartesian equation of the plane $\hat{\vec{r}} \cdot \hat{i} + \hat{j} + \hat{k} = 2$ is __________.

This is a Fill in the blanks Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n e q u a t i o n \vec{r} . (\hat{i} + \hat{j} - \hat{k}) = 2 \\ \Rightarrow (x \hat{i} + y \hat{j} + z \hat{k}) . (\hat{i} + \hat{j} - \hat{k}) = 2 \\ \Rightarrow x + y - z = 2 \\ H e n c e, t h e C a r t e s i a n e q u a t i o n o f t h e p l a n e i s x + y - z = 2 \end{array}$

Three-Dimensional Geometry True or False Type Questions

1. The unit vector normal to the plane $x + 2 y + 3 z - 6 = 0$ is $1 / \sqrt 14 \hat{i} + 2 / \sqrt 14 \hat{j} + 3 / \sqrt 14 \hat{k} .$

Ans. $\begin{array}{l} G i v e n p l a n e i s x + 2 y + 3 z - 6 = 0 \\ V e c t o r n o r m a l t o t h e p l a n e \vec{n} = \hat{i} + 2 \hat{j} + 3 \hat{k} \\ ∴ \hat{n} = \frac{\vec{n}}{| \vec{n} |} = \frac{\hat{i} + 2 \hat{j} + 3 \hat{k}}{\sqrt[]{{(1)}^{2} + {(2)}^{2} + {(3)}^{2}}} = \frac{1}{\sqrt[]{14}} \hat{i} + \frac{2}{\sqrt[]{14}} \hat{j} + \frac{3}{\sqrt[]{14}} \hat{k} \\ H e n c e, t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

2. The intercepts made by the plane $2 x - 3 y + 5 z + 4 = 0$ on the coordinate axis are $- 2, \frac{4}{3}, - \frac{4}{5}$ .

Ans. $\begin{array}{l} E q u a t i o n o f t h e p l a n e i s 2 x - 3 y + 5 z + 4 = 0 \\ \Rightarrow 2 x - 3 y + 5 z = - 4 \\ \Rightarrow \frac{2}{- 4} x - \frac{3}{- 4} y + \frac{5}{- 4} z = 1 \\ \Rightarrow \frac{x}{- 2} - \frac{y}{4 / 3} + \frac{z}{- 4 / 5} = 1 \\ S o, t h e r e q u i r e d intercepts a r e - 2, \frac{4}{3} a n d \frac{- 4}{5} \\ H e n c e, t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

Commonly asked questions

The unit vector normal to the plane $x + 2 y + 3 z - 6 = 0$ is $1 / \sqrt 14 \hat{i} + 2 / \sqrt 14 \hat{j} + 3 / \sqrt 14 \hat{k} .$

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} G i v e n p l a n e i s x + 2 y + 3 z - 6 = 0 \\ V e c t o r n o r m a l t o t h e p l a n e \vec{n} = \hat{i} + 2 \hat{j} + 3 \hat{k} \\ ∴ \hat{n} = \frac{\vec{n}}{| \vec{n} |} = \frac{\hat{i} + 2 \hat{j} + 3 \hat{k}}{\sqrt[]{{(1)}^{2} + {(2)}^{2} + {(3)}^{2}}} = \frac{1}{\sqrt[]{14}} \hat{i} + \frac{2}{\sqrt[]{14}} \hat{j} + \frac{3}{\sqrt[]{14}} \hat{k} \\ H e n c e, t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

The intercepts made by the plane $2 x - 3 y + 5 z + 4 = 0$ on the coordinate axis are $- 2, \frac{4}{3}, - \frac{4}{5}$ .

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} E q u a t i o n o f t h e p l a n e i s 2 x - 3 y + 5 z + 4 = 0 \\ \Rightarrow 2 x - 3 y + 5 z = - 4 \\ \Rightarrow \frac{2}{- 4} x - \frac{3}{- 4} y + \frac{5}{- 4} z = 1 \\ \Rightarrow \frac{x}{- 2} - \frac{y}{4 / 3} + \frac{z}{- 4 / 5} = 1 \\ S o, t h e r e q u i r e d intercepts a r e - 2, \frac{4}{3} a n d \frac{- 4}{5} \\ H e n c e, t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

The angle between the line $\vec{r} = (5 \hat{i} + 3 \hat{j} + 7 \hat{k})$ + $λ (2 \hat{i} - \hat{j} + \hat{k})$ and the plane $\vec{r} = \hat{3 i} - 4 \hat{j} - 4 \hat{k}$ + 5 = 0 is $s i n^{- 1} (5 / 2 \sqrt 91)$ . .

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} E q u a t i o n o f l i n e i s \vec{r} = (5 \hat{i} - \hat{j} - 4 \hat{k}) + λ (2 \hat{i} - \hat{j} + \hat{k}) a n d t h e \\ e q u a t i o n o f p l a n e i s \vec{r} . (3 \hat{i} - 4 \hat{j} - \hat{k}) + 5 = 0 \\ H e r e, \vec{b_{1}} = 2 \hat{i} - \hat{j} + \hat{k} a n d \vec{n_{2}} = 3 \hat{i} - 4 \hat{j} - \hat{k} \\ ∴ s i n θ = \frac{\vec{b_{1}} \vec{n_{2}}}{| \vec{b_{1}} | | \vec{n_{2}} |} \\ \Rightarrow s i n θ = \frac{(2 \hat{i} - \hat{j} + \hat{k}) . (3 \hat{i} - 4 \hat{j} - \hat{k})}{\sqrt[]{4 + 4 + 1} \sqrt[]{9 + 16 + 1}} = \frac{6 + 4 - 1}{\sqrt[]{6} \sqrt[]{26}} = \frac{9}{\sqrt[]{6} \sqrt[]{26}} \\ \Rightarrow s i n θ = \frac{9}{2 \sqrt[]{39}} w h i c h i s f a l s e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s F a l s e . \end{array}$

The angle between the planes $\vec{r} \cdot (2 \hat{i} - 3 \hat{j} + \hat{k}) = 1 and \vec{r} \cdot (\hat{i} - \hat{j}) = 4$ is $c o s^{- 1} (\frac{5}{\sqrt 58})$ .

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n p l a n e a r e \vec{r} . (2 \hat{i} - 3 \hat{j} + \hat{k}) = 1 a n d \vec{r} . (\hat{i} - \hat{j}) = 4 \\ H e r e, \vec{b_{1}} = 2 \hat{i} - 3 \hat{j} + \hat{k} a n d \vec{n_{2}} = \hat{i} - \hat{j} \\ S o, c o s θ = \frac{\vec{b_{1}} \vec{n_{2}}}{| \vec{b_{1}} | | \vec{n_{2}} |} \\ \Rightarrow c o s θ = \frac{(2 \hat{i} - 3 \hat{j} + \hat{k}) . (\hat{i} - \hat{j})}{\sqrt[]{4 + 9 + 1} \sqrt[]{1 + 1}} = \frac{2 + 3}{\sqrt[]{14} \sqrt[]{2}} = \frac{5}{\sqrt[]{28}} \\ ∴ θ = c o s^{- 1} (\frac{5}{\sqrt[]{28}}) w h i c h i s f a l s e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s F a l s e . \end{array}$

The line $\vec{r} = \hat{2 i} + \hat{3 j} + \hat{k} + λ (\hat{i} - \hat{j} + \hat{k})$ lies in the plane $\hat{r} \cdot (3 \hat{i} + \hat{j} + \hat{k}) + 2 = 0 .$

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} D i r e c t i o n r a t i o s o f t h e l i n e (\hat{i} - \hat{j} + 2 \hat{k}) \\ D i r e c t i o n r a t i o s o f t h e n o r m a l t o t h e p l a n e a r e (3 \hat{i} + \hat{j} - \hat{k}) \\ S o, (\hat{i} - \hat{j} + 2 \hat{k}) . (3 \hat{i} + \hat{j} - \hat{k}) = 3 - 1 - 2 = 0 \\ T h e r e f o r e, t h e l i n e i s p a r a l l e l t o t h e p l a n e . \\ N o w point t h r o u g h w h i c h t h e l i n e i s passing \to =2 \hat{i} - 3 \hat{j} - \hat{k} \\ I f t h e l i n e l i e s i n t h e p l a n e t h e n \\ (2 \hat{i} - 3 \hat{j} - \hat{k}) . (3 \hat{i} + \hat{j} - \hat{k}) + 2 = 0 \\ 6 - 3 + 1 + 2 \neq 0 \\ S o, t h e l i n e d o e s n o t l i e i n t h e p l a n e . \\ H e n c e, t h e g i v e n s t a t e m e n t i s F a l s e . \end{array}$

The vector equation of the line $\frac{x - 5}{3} = \frac{y - 4}{7} = \frac{z - 6}{2}$ is $\hat{r} = 5 \hat{i} - 4 \hat{j} + 6 \hat{k} + λ (3 \hat{i} + 7 \hat{j} + 2 \hat{k}) .$

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e C a r t e s i a n f o r m o f t h e e q u a t i o n i s \\ \frac{x - 5}{3} = \frac{y + 4}{7} = \frac{z - 6}{2} = λ \\ H e r e, x_{1} = 5, y_{1} = - 4, z_{1} = 6; a = 3, b = 7, c = 2 \\ S o, t h e v e c t o r e q u a t i o n i s \vec{r} = (5 \hat{i} - 4 \hat{j} + 6 \hat{k}) + λ (3 \hat{i} + 7 \hat{j} + 2 \hat{k}) \\ H e n c e, t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

The equation of a line, which is parallel to $2 \hat{i} + \hat{j} + \hat{3 k}$ and passes through the point (5, –2, 4), is $\frac{x - 5}{2} = \frac{y + 2}{- 1} = \frac{z - 4}{3} .$

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} H e r e, x_{1} = 5, y_{1} = - 2, z_{1} = 4; a = 2, b = 1, c = 3 \\ W e k n o w t h a t t h e e q u a t i o n o f l i n e i s \frac{x - x_{1}}{a} = \frac{y - y_{1}}{b} = \frac{z - z_{1}}{c} \\ \Rightarrow \frac{x - 5}{2} = \frac{y + 2}{1} = \frac{z - 4}{3} \\ H e n c e, t h e g i v e n s t a t e m e n t i s F a l s e . \end{array}$

If the foot of the perpendicular drawn from the origin to a plane is (5, –3, –2), then the equation of the plane is $\vec{r} \cdot (5 \hat{i} - 3 \hat{j} + 2 \hat{k}) - 38 .$

This is a True or False Type Questions as classified in NCERT Exemplar

$\begin{array}{l} T h e g i v e n e q u a t i o n o f t h e p l a n e i s \vec{r} . (5 \hat{i} - 3 \hat{j} - 2 \hat{k}) = 38 \\ I f t h e f o o t o f t h e p e r p e n d i c u l a r t o t h i s p l a n e i s \\ (5, - 3, - 2) i . e ., 5 \hat{i} - 3 \hat{j} - 2 \hat{k} t h e n \\ \Rightarrow (5 \hat{i} - 3 \hat{j} - 2 \hat{k}) . (5 \hat{i} - 3 \hat{j} - 2 \hat{k}) = 38 \\ \Rightarrow 25 + 9 + 4 = 38 \\ 38 = 38 (s a t i s f i e d) \\ H e n c e, t h e g i v e n s t a t e m e n t i s T r u e . \end{array}$

Maths NCERT Exemplar Solutions Class 12th Chapter Eleven Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Three Dimensional Geometry

News & Updates

Latest NewsPopular News

Maths NCERT Exemplar Solutions Class 12th Chapter Eleven: Overview, Questions, Preparation

Three-Dimensional Geometry Long Answer Type Questions

Commonly asked questions

Three-Dimensional Geometry Short Answer Type Questions

Commonly asked questions

Three-Dimensional Geometry Objective Type Questions

Commonly asked questions

Three-Dimensional Geometry Fill in the blanks Type Questions

Commonly asked questions

Three-Dimensional Geometry True or False Type Questions

Commonly asked questions

Student Forum

Other Similar chapters for you

News & Updates

TS SSC Exam Time table 2026 Soon @bse.telangana.gov.in; Live Updates on Telangana SSC Board Exam Dates

Uttarakhand Class 10, 12 Exam Dates 2026 Soon @ubse.uk.gov.in! Check Live updates on UK Board Date Sheet 2026

Scope of Fashion Technology through NIFT

TNTET 2025 Answer Key Anytime Soon: Check Expected Release Date

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement