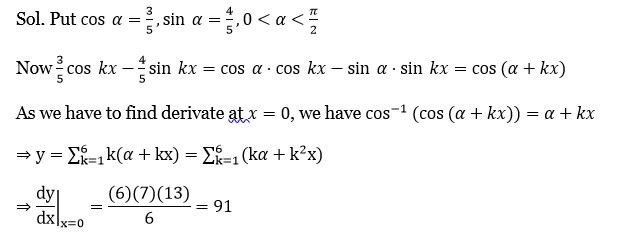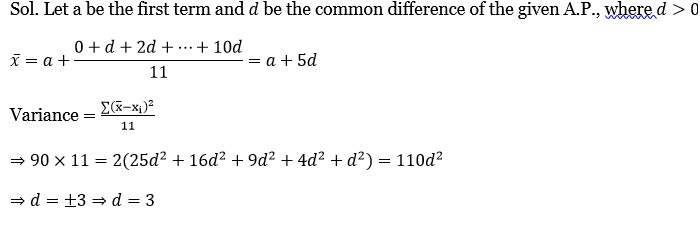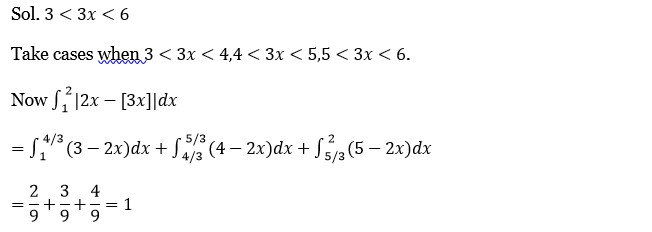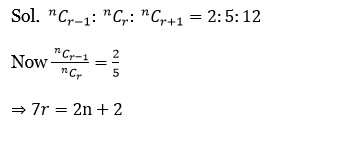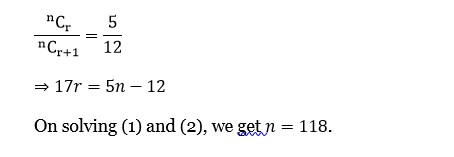- Principle of Mathematical Induction Long Answer Type Questions
- Principle of Mathematical Induction Short Answer Type Questions
- Principle of Mathematical Induction Objective Type Questions
- Jee mains
Principle of Mathematical Induction Long Answer Type Questions
| A sequence is defined by letting and , for all . Show that , for all . |
| A sequence is defined by letting and , for all . Show that , for all . |
Commonly asked questions
A sequence is defined by letting and , for all . Show that , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
A sequence is defined by letting and , for all . Show that , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
A sequence is defined by letting and , for all . Show that , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that, for all :
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Show that
is a natural number, for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that the number of subsets of a set containing distinct elements is , for all .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If y = Σ???? kcos?¹{ (3/5)coskx - (4/5)sinkx }, then dy/dx at x=0 is
Kindly consider the following Image
If the variance of the terms in an increasing A.P. b?,b?,b?,...,b?? is 90, then the common difference of this A.P. is
Kindly consider the following Image
Let [t] denote the greatest integer less than or equal to t. Then the value of ∫?²|2x-[3x]|dx is
Kindly consider the following Image
For a positive integer n, (1+x/2)? is expanded in increasing powers of x. If three consecutive coefficients in this expansion are in the ratio 2:5:12, then n is equal to
Kindly consider the following Image
Let the position vectors of points 'A' and 'B' be i+j+k and 2i+j+3k, respectively. A point 'P' divides the line segment AB internally in the ratio λ:1(λ>0). If O is the origin and OB.OP - 3|OA×OP|² = 6, then λ is equal to
Kindly consider the following Image
Principle of Mathematical Induction Short Answer Type Questions
| Give an example of a statement which is true for all but , , and are not true. Justify your answer. |
| Give an example of a statement which is true for all . Justify your answer. |
Commonly asked questions
Give an example of a statement which is true for all but , , and are not true. Justify your answer.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Give an example of a statement which is true for all . Justify your answer.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
For any natural numbers is divisible by x-y where x and y are any integers with x≠y.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
is divisible by 3, for each natural number .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
is divisible by 7, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
is divisible by 3, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
is divisible by 8, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
For any natural numbers is divisible by 5.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
is divisible by 6, for each natural number .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
is divisible by 6, for each natural number .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
, for all natural numbers .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Principle of Mathematical Induction Objective Type Questions
| If is divisible by 9 for all , then the least positive integral value of is: (a) 5 (b) 3 (c) 7 (d) 1 |
| For all , is divisible by: (a) 9 (b) 17 (c) 23 (d) 25 |
Commonly asked questions
If is divisible by 9 for all , then the least positive integral value of is:
(a) 5
(b) 3
(c) 7
(d) 1
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
For all , is divisible by:
(a) 19
(b) 17
(c) 23
(d) 25
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If is divisible by , then the least positive integral value of is:
(a) 1
(b) 2
(c) 3
(d) 4
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If , , then is true for all ____.
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Let be a statement and let P(k + 1) for some natural number . Then is true for all .
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Jee mains
Jee mains
Maths NCERT Exemplar Solutions Class 11th Chapter Four Exam