- Straight Limes Short Answer Type Questions
- Straight Limes Long Answer Type Questions
- Straight Limes Objective Type Questions
- Straight Limes Fill in the Blank
- Straight Limes True or False Type Questions
- JEE MAINS 26th February 2021 First Shift
- JEE Mains 2025
Straight Limes Short Answer Type Questions
| Find the equation of the straight line which passes through the point (1, –2) and cuts off equal intercepts from axes. |
| Sol:
|
| Find the equation of the line passing through the point (5, 2) and perpendicular to the line joining the points (2, 3) and (3, –1). |
| Sol:
|
Commonly asked questions
Find the equation of the straight line which passes through the point (1, –2) and cuts off equal intercepts from axes.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If the intercept of a line between the coordinate axes is divided by the point (–5, 4) in the ratio 1: 2, then find the equation of the line.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of a straight line on which the length of perpendicular from the origin is four units and the line makes an angle of 120° with the positive direction of the x-axis.
(Hint: Use normal form, where ω = 30°.)
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the line passing through the point (5, 2) and perpendicular to the line joining the points (2, 3) and (3, –1).
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the angle between the lines y = (2 – 3)(x + 5) and y = (2 + 3)(x – 7).
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the lines which passes through the point (3, 4) and cuts off intercepts from the coordinate axes such that their sum is 14.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the points on the line x + y = 4 which lie at a unit distance from the line 4x + 3y = 10.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Show that the tangent of an angle between the lines x/a + y/b = 1 and x/a − y/b = 1 is 2ab / (a² − b²).
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of lines passing through (1, 2) and making an angle 30° with the y-axis.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the line passing through the point of intersection of 2x + y = 5 and x + 3y + 8 = 0 and parallel to the line 3x + 4y = 7.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
For what values of a and b the intercepts cut off on the coordinate axes by the line ax + by + 8 = 0 are equal in length but opposite in signs to those cut off by the line 2x – 3y + 6 = 0 on the axes.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of one of the sides of an isosceles right-angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2, 2).
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Straight Limes Long Answer Type Questions
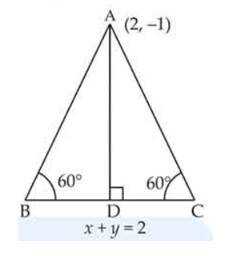
| If the equation of the base of an equilateral triangle is x + y = 2 and the vertex is (2, –1), then find the length of the side of the triangle. (Hint: Find the length of the perpendicular (p) from (2, –1) to the line and use p = l sin 60°, where l is the length of the side of the triangle.) |
| Sol:
|
| A variable line passes through a fixed-point P. The algebraic sum of the perpendiculars drawn from the points (2, 0), (0, 2), and (1, 1) on the line is zero. Find the coordinates of the point P. (Hint: Let the slope of the line be m. Then the equation of the line passing through the fixed-point P (x₁, y₁) is y – y ₁ = m (x – x₁). Taking the algebraic sum of perpendicular distances equal to zero, we get y – 1 = m (x – 1). Thus (x₁, y₁) is (1, 1). |
| Sol:
|
Commonly asked questions
If the equation of the base of an equilateral triangle is x + y = 2 and the vertex is (2, –1), then find the length of the side of the triangle.
(Hint: Find the length of the perpendicular (p) from (2, –1) to the line and use p = l sin 60°, where l is the length of the side of the triangle.)
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
A straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point.
(Hint: 1/a+1/b=1, where a + b =” constant” =1/k (say). This implies that a + b = k. Line passes through the fixed point (k, k).)
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If the sum of the distances of a moving point in a plane from the axes is 1, then find the locus of the point.
(Hint: Given that x + y = 1, which gives four sides of a square.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
P1, P2 are points on either of the two lines y – 3x = 2 at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P?, P? on the bisector of the angle between the given lines.
(Hint: Lines are y = x + 2 and y = – x + 2 according as x ≥ 0 or x < 0
Y-axis is the bisector of the angles between the lines. P?, P? are the points on these lines at a distance of 5 units from the point of intersection of these lines which have a point on y-axis as the common foot of perpendiculars from these points. The y-coordinate of the foot of the perpendicular is given by 2 + 5 cos30°.)
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If p is the length of perpendicular from the origin on the line =1 and are in A.P., then show that =0.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
A variable line passes through a fixed-point P. The algebraic sum of the perpendiculars drawn from the points (2, 0), (0, 2), and (1, 1) on the line is zero. Find the coordinates of the point P.
(Hint: Let the slope of the line be m. Then the equation of the line passing through the fixed-point P (x?, y?) is y – y ? = m (x – x?). Taking the algebraic sum of perpendicular distances equal to zero, we get y – 1 = m (x – 1). Thus (x?, y?) is (1, 1).
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
In what direction should a line be drawn through the point (1, 2) so that its point of intersection with the line x + y = 4 is at a distance √5 from the given point?
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the equation of the line which passes through the point (–4, 3), and the portion of the line intercepted between the axes is divided internally in the ratio 5: 3 by this point.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
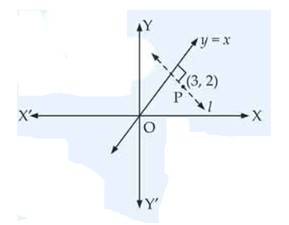
Find the equations of the lines through the point of intersection of the lines x – y + 1 = 0 and 2x – 3y + 5 = 0 and whose distance from the point (3, 2) is √5.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Straight Limes Objective Type Questions
| A line cutting off intercept –3 from the y-axis and the tangent at angle θ to the x-axis is tanθ = , its equation is (a) 5y-3x+15=0 (b) 3y-5x+15=0 (c) 5y-3x-15=0 (d) None of these |
| Sol:
|
| Slope of a line which cuts off intercepts of equal lengths on the axes is (a) -1 (b) -0 (c) 2 (d) 3 |
| Sol:
|
Commonly asked questions
A line cutting off intercept –3 from the y-axis and the tangent at angle θ to the x-axis is tanθ = , its equation is
(a) 5y-3x+15=0
(b) 3y-5x+15=0
(c) 5y-3x-15=0
(d) None of these
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Slope of a line which cuts off intercepts of equal lengths on the axes is
(a) -1
(b) -0
(c) 2
(d) 3
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The equation of the straight line passing through the point (3, 2) and perpendicular to the line y=x is
(a) X-y=5
(b) X+y=5
(c) X+y=1
(d) X-y=1
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The equation of the line passing through the point (1, 2) and perpendicular to the line x+y+1=0 is
(a) Y-x+1=0
(b) Y-x-1=0
(c) Y-x+2=0
(d) Y-x-2=0
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The tangent of angle between the lines whose intercepts on the axes are (a,-b) and (b,-a), respectively, is
(a)
(b)
(c)
(d) None of these
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If the line passes through the points (2, –3) and (4, –5), then (a, b) is
(a) (1, 1)
(b) (–1, 1)
(c) (1, –1)
(d) (–1, –1)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The distance of the point of intersection of the lines 2x – 3y + 5 = 0 and 3x + 4y = 0 from the line 5x – 2y = 0 is
(a)
(b)
(c)
(d) None of these
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The equations of the lines which pass through the point (3, –2) and are inclined at 60° to the line 3x + y = 1 is
(a)
(b)
(c)
(d) None of these
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The equations of the lines passing through the point (1, 0) and at a distance from the origin, are
(a)
(b)
(c)
(d) None of these
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The distance between the lines and is
(a)
(b)
(c)
(d) 0
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The coordinates of the foot of the perpendicular from the point (2, 3) on the line is given by
(a)
(b)
(c)
(d)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If the coordinates of the middle point of the portion of a line intercepted between the coordinate axes is (3, 2), then the equation of the line will be
(a) 2x + 3y = 12
(b) 3x + 2y = 12
(c) 4x – 3y = 6
(d) 5x – 2y = 10
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is
(a) y + 2 = x + 1
(b) y + 2 = 3 (x + 1)
(c) y – 2 = 3 (x – 1)
(d) y – 2 = x – 1
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Equations of diagonals of the square formed by the lines x = 0, y = 0, x = 1, and y = 1 are
(a) y = x, y + x = 1
(b) y = x, x + y = 2
(c) 2y = x, y + x =
(d) y = 2x, y + 2x = 1
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
For specifying a straight line, how many geometrical parameters should be known?
(a) 1
(b) 2
(c) 4
(d) 3
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The point (4, 1) undergoes the following two successive transformations:
i. Reflection about the line y = x
ii. Translation through a distance 2 units along the positive x-axis
Then the final coordinates of the point are
(a) (4, 3)
(b) (3, 4)
(c) (1, 4)
(d)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A point equidistant from the lines 4x + 3y + 10 = 0, 5x – 12y + 26 = 0, and 7x + 24y – 50 = 0 is
(a) (1, –1)
(b) (1, 1)
(c) (0, 0)
(d) (0, 1)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A line passes through (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is
(a)
(b)
(c) 1
(d)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The ratio in which the line 3x + 4y + 2 = 0 divides the distance between the lines 3x + 4y + 5 = 0 and 3x + 4y – 5 = 0 is
(a) 1 : 2
(b) 3 : 7
(c) 2 : 3
(d) 2 : 5
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
One vertex of the equilateral triangle with centroid at the origin and one side as x + y – 2 = 0 is
(a) (–1, –1)
(b) (2, 2)
(c) (–2, –2)
(d) (2, –2)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Straight Limes Fill in the Blank
| If a, b, c are in A.P., then the straight lines ax + by + c = 0 will always pass through ____. |
| Sol:
|
| The line which cuts off equal intercepts from the axes and passes through the point (1, –2) is ____. |
| Sol:
|
Commonly asked questions
If a, b, c are in A.P., then the straight lines ax + by + c = 0 will always pass through ____.
This is a Fill in the Blank Type Questions as classified in NCERT Exemplar
Sol:
The line which cuts off equal intercepts from the axes and passes through the point (1, –2) is ____.
This is a Fill in the Blank Type Questions as classified in NCERT Exemplar
Sol:
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ____.
This is a Fill in the Blank Type Questions as classified in NCERT Exemplar
Sol:
The points (3, 4) and (2, –6) are situated on the ____ of the line 3x – 4y – 8 = 0.
This is a Fill in the Blank Type Questions as classified in NCERT Exemplar
Sol:
A point moves so that the square of its distance from the point (3, –2) is numerically equal to its distance from the line 5x – 12y = 3. The equation of its locus is ____.
This is a Fill in the Blank Type Questions as classified in NCERT Exemplar
Sol:
Locus of the midpoints of the portion of the line intercepted between the axes is ____.
This is a Fill in the Blank Type Questions as classified in NCERT Exemplar
Sol:
Straight Limes True or False Type Questions
| If the vertices of a triangle have integral coordinates, then the triangle cannot be equilateral. |
| Sol:
|
| The points A(–2, 1), B(0, 5), C(–1, 2) are collinear. |
| Sol:
|
Commonly asked questions
If the vertices of a triangle have integral coordinates, then the triangle cannot be equilateral.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The points A(–2, 1), B(0, 5), C(–1, 2) are collinear.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
Equation of the line passing through the point and perpendicular to the line is .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The straight line 5x + 4y = 0 passes through the point of intersection of the straight lines x + 2y – 10 = 0 and 2x + y + 5 = 0.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The vertex of an equilateral triangle is (2, 3) and the equation of the opposite side is x + y = 2. Then the other two sides are .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The equation of the line joining the point (3, 5) to the point of intersection of the lines 4x + y – 1 = 0 and 7x – 3y – 35 = 0 is equidistant from the points (0, 0) and (8, 34).
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The line moves in such a way that , where c is a constant. The locus of the foot of the perpendicular from the origin on the given line is .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The lines and are concurrent if a, b, c are in G.P.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The line joining the points (3, –4) and (–2, 6) is perpendicular to the line joining the points (–3, 6) and (9, –18).
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
Match the following:
Column C1 Column C2
(a) The coordinates of the points P and Q on the (i)
line , which are at a distance of 2 units
from the line are
(b) The coordinates of the point on the (ii)
line , which is at a unit distance
from the line .
(c) The coordinates of the point on the line (iii)
joining A(–2, 5) and B(3, 1) such that
are
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The value of , if the lines are
Column C1 Column C2
i. Parallel to y-axis is (i)
ii. Perpendicular to is (ii)
iii. passes through (1, 2) is (iii)
iv. parallel to x-axis is (iv)
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
The equation of the line through the intersection of the lines and and
Column C1Column C2
through the point (2, 1) is (i)
perpendicular to the line is (ii)
parallel to the line is (iii)
equally inclined to the axes is (iv)
Sol:
JEE MAINS 26th February 2021 First Shift
JEE MAINS 26th February 2021 First Shift
Commonly asked questions
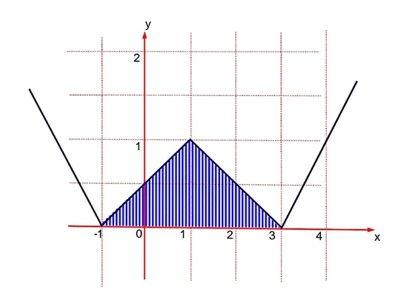
The area bounded by the lines y = is-----------.
Information missing. The question was droppedby NTA.
Area bounded region =
If the number of solutions of the given equation when x is------.
Hence, cos x = 1 x = 0 one solution
The number of solution of the log4 (x-1) = log2 (x-3) is------------.
also x – 1 > 0 and x – 3 > 0
x > 1 & x > 3
Hence, x = 5 possible. Only one solution.
If y = y(x) is the solution of the equation esin y then is equal to----------.
Put esin y = t
Put sin x = u, cos xdx = du
Let be a point on the plane which passes which through the point (4, 2, 2). If the plane is perpendicular to the line joining the points (2, 21, 29) and (1, 16, 23), then is equal to----------.
Let
Given
The number of integral values of ‘k’ for which the equation 3sinx + 4cos x = k + 1 has a solution, k R is------------.
total number of integral values of k is 11.
The sum of 162th power of the roots of the equation -------------.
Sum of 162th power of roots =
Let m, n N and gcd (2, n) = 1. If 30 = n. 2m, then n + m is equal to--------.
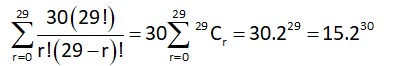
The difference between degree and order of a differential equation that represents the family of curves given by y2 = a --------------.
2yy1 = a
Hence, degree – order = 3 – 1 = 2
The value of the integral -----------.
=2 =
JEE Mains 2025
JEE Mains 2025
Maths NCERT Exemplar Solutions Class 11th Chapter Ten Exam