
- Trigonometric Functions Short Answer Type Questions
- Trigonometric Functions Long Answer Type Questions
- Trigonometric Functions Objective Type Questions
- Trigonometric Functions Fill in the blanks Type Questions
- Trigonometric Functions True or False Type Questions
- JEE Mains 2020
Trigonometric Functions Short Answer Type Questions
| 1. Prove that |
| Sol:
|
| 2. If then prove that [Hint: Express |
| Sol:
|
Commonly asked questions
Prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If then prove that
[Hint: Express
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If , then prove that
[Hint: Express and apply componendo and dividendo.]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , where lies between and , find the value of .
[Hint: Express as .]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
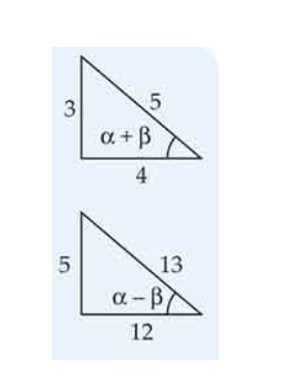
If , then find the value of
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , then show that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the value of .
[Hint: Use .]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , then prove that
[Hint: Use and ., then use ]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If , , then show that
[Hint: Use .]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , then prove that
[Hint: Use .]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If then show that
[Hint: Use Componendo and Dividendo.]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If then show that
[Hint: Express the given equation as .]
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If , then find the general value of .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the most general value of satisfying the equation
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If , then find the general value of .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If , where , then find the value of .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If where , then find the value of .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Trigonometric Functions Long Answer Type Questions
| 1. If and , then prove that Hint: Express cos cos (( ) )] |
| Sol:
|
| 2. If , then prove that tan [Hint: Express .]and apply componendo and dividendo.] |
| Sol:
|
Commonly asked questions
If and , then prove that
Hint: Express cos cos (( ) )]
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If , then prove that tan
[Hint: Express .]and apply componendo and dividendo.]
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the value of the expression
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If has and as its roots, then prove that
[Hint: Use the identities for and = ]
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If lies in the first quadrant and , then find the value of
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the value of the expression
Hint : Simplify the expression to 2 (
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the general solution of the equation
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the general solution of the equation
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the general solution of the equation
[Hint: Put . ]
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Trigonometric Functions Objective Type Questions
| Choose the correct answer from the given four options in each of the Exercises 30 to 59: 1. If , then is equal to: (a) 1 (b) 4 (c) 2 (d) None of these |
| Sol:
|
| 2. If , then: (a) (b) (c) (d) f(x) [Hint: A.M ≥ G.M.] |
|
Sol:
|
Commonly asked questions
Choose the correct answer from the given four options in each of the Exercises 30 to 59:
If , then is equal to:
(a) 1
(b) 4
(c) 2
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If , then:
(a)
(b)
(c)
(d) f(x)
[Hint: A.M ≥ G.M.]
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If and , then the value of is:
(a)
(b)
(c) 0
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
Which of the following is not correct?
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exempar
Sol:
The value of is:
(a) 0
(b) 1
(c) 2
(d) Not defined
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is:
(a) 1
(b)
(c)
(d) 2
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is:
(a)
(b) 0
(c) 1
(d) -1
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If and lies in the third quadrant, then the value of is:
(a)
(b)
(c)
(d)
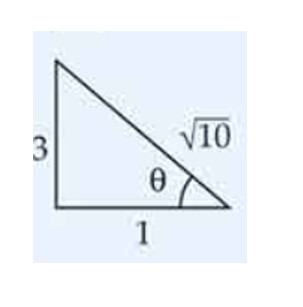
The value of is equal to:
(a)
(b)
(c)
(d) 1
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
Which of the following is correct?
(a)
(b)
(c)
(d)
Hint 1 radian =
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If and , then is equal to:
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The minimum value of is:
(a) 5
(b) 9
(c) 7
(d) 3
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of tan 3A -tan2A-tanA is equal to
(a) tan3Atan2AtanA
(b) -tan3Atan2AtanA
(c) tanAtan2A-tan2Atan3A-tan3AtanA
(d) None of these
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is:
(a)
(b)
(c) 1
(d) 0
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is:
(a)
(b)
(c)
(d) Not defined
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
is equal to:
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is:
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If and , then is equal to:
(a) 1
(b) 2
(c) 3
(d) 4
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is:
(a)
(b)
(c)
(d) 1
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is equal to:
(a) 1
(b) 0
(c)
(d) 1
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If , then the value of is:
(a) 1
(b)
(c) 0
(d) -1
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If , then the value of is:
(a) 1
(b) 2
(c) -2
(d) Not defined
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If and lies in the third quadrant, then the value of is:
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
Number of solutions of the equation lying in the interval is:
(a) 0
(b) 1
(c) 2
(d) 3
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
The value of is given by:
(a) 1
(b) -1
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If lies in the second quadrant and , then the value of is equal to:
(a)
(b)
(c)
(d) None
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
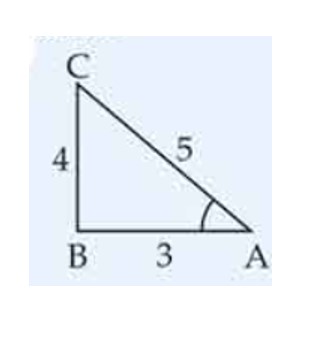
The value of is:
(a)
(b)
(c)
(d)
Hint : Use of
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If , , then is equal to:
(a)
(b)
(c)
(d)
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If , then is equal to:
(a) a
(b) b
(c)
(d) None
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
If , then is:
(a) An acute angle
(b) A right angle
(c) An obtuse angle
(d) Not possible
This is an Objective Type Questions as classified in NCERT Exemplar
Sol:
Trigonometric Functions Fill in the blanks Type Questions
| 1. The value of is ___. |
| Sol:
|
| 2. If , then the numerical value of is ___. |
| Sol:
|
Commonly asked questions
The value of is ___.
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
If , then the numerical value of is ___.
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
If , then is ___.
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
If , then:
i. ___
ii. ___
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
In a triangle with , the equation whose roots are and is ___.
Hint :If , then ___.
This is a Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
___.
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
Given , the values of lie in the interval ___.
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
The maximum distance of a point on the graph of the function from the -axis is ___.
This is an Fill in the blanks Type Questions as classified in NCERT Exemplar
Sol:
Trigonometric Functions True or False Type Questions
| 1. If , then . |
| Sol:
|
| 2. The equality holds for some real value of . |
| Sol:
|
Commonly asked questions
If , then .
This is an True or False Type Questions as classified in NCERT Exemplar
Sol:
The equality holds for some real value of .
This is an True or False Type Questions as classified in NCERT Exemplar
Sol:
is greater than .
This is an True or False Type Questions as classified in NCERT Exemplar
Sol:
.
This is an True or False Type Questions as classified in NCERT Exemplar
Sol:
One value of which satisfies the equation lies between and .
This is an True or False Type Questions as classified in NCERT Exemplar
Sol:
If , then .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If , then .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If , then .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
Match the following items under column to their correct answers under column :
i. (i)
ii. (ii)
iii. (iii)
iv. (iv)
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
JEE Mains 2020
JEE Mains 2020
Maths NCERT Exemplar Solutions Class 11th Chapter Three Exam
