- Continuity and Differentiability Questions and Answers
- JEE Mains Solutions 2022,29th june , Maths, first shift
- JEE Mains 2022
- JEE Mains 2022
Continuity and Differentiability Questions and Answers
| Q1. Find the values of and so that is differentiable at . |
| Sol:
|
| Q2. If , prove that (i) (ii) . |
| Sol:
|
| Q3. If and , prove that |
| Sol:
|
Q4. 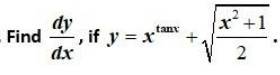 |
| Sol: |
Commonly asked questions
Find the values of and so that is differentiable at .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If , prove that
(i)
(ii)
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , prove that
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
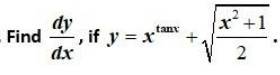
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

Examine the continuity of the function
at
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find which of the functions in Exercises 2 to 10 is continuous or discontinuous at the indicated points:
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at ,
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at ,
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at ,
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at ,
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the value of in each of the Exercises 11 to 14 so that the function is continuous at the indicated point:
at
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
at
Kindly go through the solution
Sol:
Prove that the function defined by remains discontinuous at , regardless of the choice of .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the values of and such that the function defined by
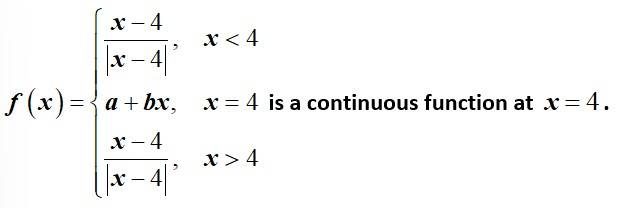
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Given the function . Find the points of discontinuity of the composite function
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find all points of discontinuity of the function where
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Show that the function is continuous at .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Examine the differentiability of , where is defined by
at .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Examine the differentiability of , where is defined by
at
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Examine the differentiability of , where is defined by
at
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Show that is continuous but not differentiable at .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A function satisfies the equation for all , where . Suppose that the function is differentiable at and .
Prove that .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Differentiate each of the following w.r.t. (Exercises 25 to 43):
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
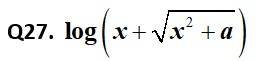
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
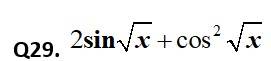
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
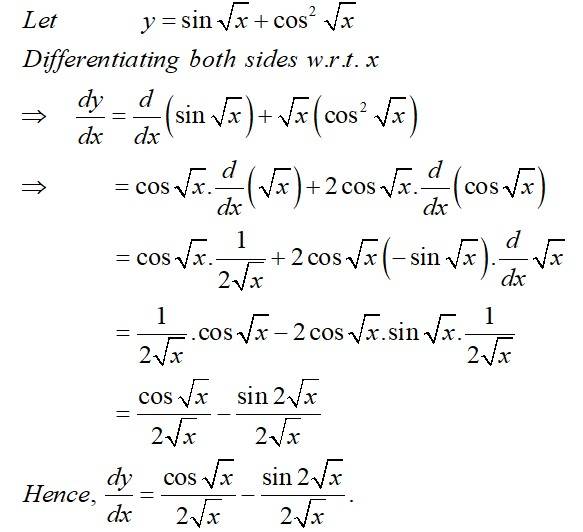
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following

This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
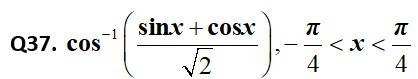
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
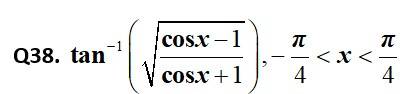
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
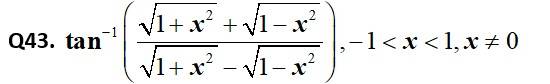
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:


Find of each of the functions expressed in parametric form in Exercises from 44 to 48.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

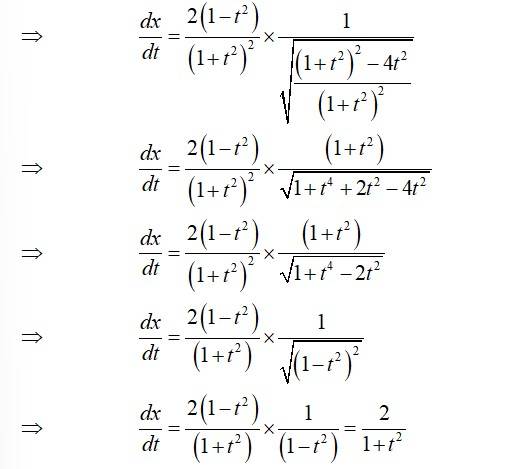
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If and , show that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If , find at .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Differentiate w.r.t. .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
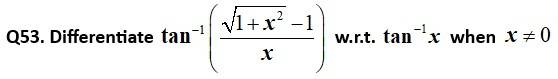
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Find when and are connected by the relation given in each of the Exercises 54 to 57.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
If , then show that .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
If , prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
If , prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
If , show that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
If , prove that
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
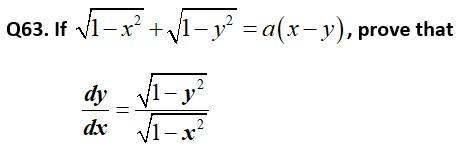
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:


Kindly consider the following
If , find in terms of alone.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Verify Rolle's theorem for each of the functions in Exercises 65 to 69.
in
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
in
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
in
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
in .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
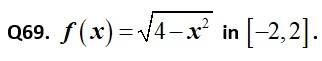
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Discuss the applicability of Rolle’s theorem on the function given by
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the points on the curve in , where the tangent is parallel to the x-axis.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Using Rolle’s theorem, find the point on the curve , , where the tangent is parallel to the x-axis.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Verify the Mean Value Theorem for each of the functions given in Exercises 73 to 76.
in .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
in .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Kindly consider the following
in .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
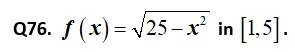
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

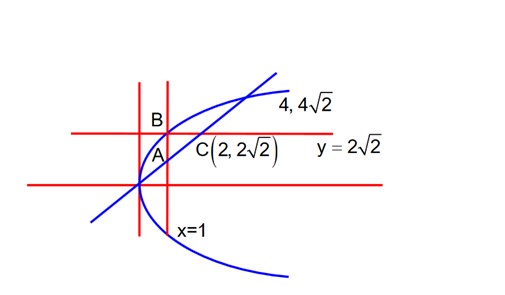
Find a point on the curve , where the tangent is parallel to the chord joining the points and .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Using the Mean Value Theorem, prove that there is a point on the curve between the points and , where the tangent is parallel to the chord . Also, find that point.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Choose the correct answer from given four options in each of the Exercises from 83 to 96.
If and , then which of the following can be a discontinuous function:
(A)
(B)
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
The function is
(A) Discontinuous at only one point
(B) Discontinuous at exactly two points
(C) Discontinuous at exactly three points
(D) None of these
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
The set of points where the function is differentiable is
(A) R
(B) R
(C)
(D) None of these
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
The function is discontinuous on the set
(A)
(B)
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
The function is
(A) Continuous everywhere but not differentiable at
(B) Continuous and differentiable everywhere
(C) Not continuous at
(D) None of these
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
If , where , then the value of the function at , so that the function is continuous at , is
(A) 0
(B) -1
(C) 1
(D) None of these
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
If is continuous at , then
(A)
(B)
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
Let . Then
(A) is everywhere differentiable
(B) is everywhere continuous but not differentiable at .
(C) is everywhere continuous but not differentiable at .
(D) None of these
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
If , then is equal to
(A)
(B)
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
If , then is equal to
(A)
(B)
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
![]()
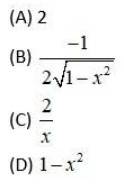
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:

If , then is
(A)
(B)
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
The value of in Rolle's theorem for the function in the interval is
(A) 1
(B) -1
(C)
(D)
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:
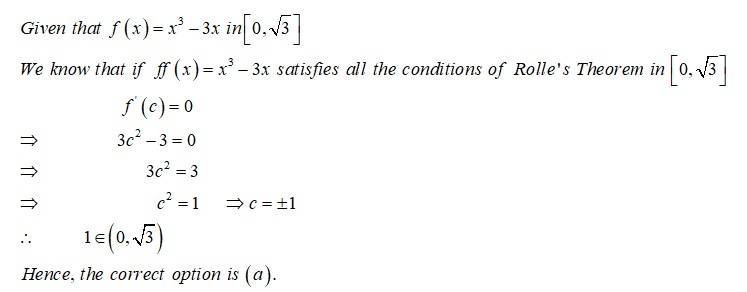
For the function , , the value of for the Mean Value Theorem is
(A) 1
(B) 3
(C) 2
(D) None of these
This is an Objective Answer Type Questions as classified in NCERT Exemplar
Sol:

An example of a function which is continuous everywhere but fails to be differentiable exactly at two points is __________.
This is a Fill in the Blanks Type questions as classified in NCERT Exemplar
Sol:
Derivative of w.r.t. is __________.
This is a Fill in the Blanks Type questions as classified in NCERT Exemplar
Sol:
If , then __________.
This is a Fill in the Blanks Type questions as classified in NCERT Exemplar
Sol:

Kindly consider the following
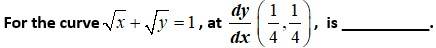
This is a Fill in the Blanks Type questions as classified in NCERT Exemplar
Sol:

State True or False for the statements in each of the Exercises 102 to 106:
Rolle’s theorem is applicable for the function in .
This is a True or False Type questions as classified in NCERT Exemplar
Sol:
If is continuous on its domain , then is also continuous on .
This is a True or False Type questions as classified in NCERT Exemplar
Sol:
The composition of two continuous functions is a continuous function.
This is a True or False Type questions as classified in NCERT Exemplar
Sol:
Trigonometric and inverse-trigonometric functions are differentiable in their respective domains.
This is a True or False Type questions as classified in NCERT Exemplar
Sol:
If is continuous at , then and are separately continuous at x=a.
This is a True or False Type questions as classified in NCERT Exemplar
Sol:
JEE Mains Solutions 2022,29th june , Maths, first shift
JEE Mains Solutions 2022,29th june , Maths, first shift
Commonly asked questions
The probability that a randomly chosen 2 × 2 matrix with all the entries from the set of first 10 primes, is singular, is equal to:
Set of first 10 prime numbers
= {2,3,5,7,11,13,17,19,23,29,31}
So sample space = 104.
Favourable cases
So required probability
Let the solution curve of the differential equation
Then y(2) is equal to:
Put y =
differentiable worst = x
V +
apply variable separable method
Given y(1) = 3 C = 8
Now at x = 2
y2 + 64 = (32 – y)2
y = 15
If the mirror image of the point (2, 4,7) in the plane 3x – y + 4z = 2 is (a, b, c), then 2a + b + 2c is equal to:
Image of pt (2,4,7) in the plane 3x – y + 4z = 2 is
Let
Now according to the question
(a, b, c) =
Now
=
= 28 + 22 [Use ]
= 6
Let f : R R be a function defined by:
where [t] is the greatest integer less than or equal to t. Let me be the number of points where f is not differentiable and Then the ordered pair (m, I) is equal to:
Draw g(t) = t3 – 3t
g’(t) = 3(t2 – 1)
g(1) is maximum in (-2, 2)
So, maximum (t3 – 3t) =
=
I =
again rewrite the f(x)
So f(x) is not differentiable at x = 2, 3, 4, 5
so m = 4
Let be three vectors. If the projection of then the value of + is equal to:
So = 1
The area enclosed by y2 = 8x and y = that lies outside the triangle formed by y = x = 1, is equal to:
Area of
=
now required area
If the system of linear equations
2x + y – z = 7
x – 3y + 2z = 1
x + 4y + where
has infinitely many solutions, then is equal to:
and
Let a and b be the roots of the equation x2 + (2i – 1) = 0. Then, the value of is equal to:
x2 = 1 – 2i
so 2 = 1 – 2i = 2
8 = 8
now
Let be such that is a tautology. Then is equal to:
=
=
=
=
now
pq
TTTTT
TFFFT
FTFTT
FFFTT
So,
Let A = be a square matrix of order 3 such that aij = 2ji, for all I, j = 1, 2, 3. Then, the matrix is equal to:
A2 = 3A
A3 = 3A2
A3 = 32A
A4 = 33A
An = 3n-1A
now, A2 + A3 +….+A10
= 3A + 32 A +….. + 39A
= 3A (1 + 3 +….+ 38
Let a set A = A1 A2 …. Ak, where Ai Aj = for Define the reaction R from A to A by R = Then, R is:
Use aRb = a is related to b, belongs to A iff a belongs to A.
In simple terms, aRb is true if both a & b belongs to the same set.
For reflexive
aRa, a
For symmetric
Let aRb be true
Þ a & b belongs to the same set.
Þ b & a also belongs to the same set
Þ bRa will be true
For transitive
Let aRb and bRc be true.
aRb Þ a, b belongs to the same set
bRc Þ b, c belongs to the same set
Þ (a, c) belongs to the same set
Þ so aRc will be true.
So R is an equivalence relation.
Let be a sequence such that a0 = a1 = 0 and an+2 = 2an+1 – an + 1 for all Then, is equal to:
a2 = 1
a3 = 3
a4 = 6
So for n
Let S =
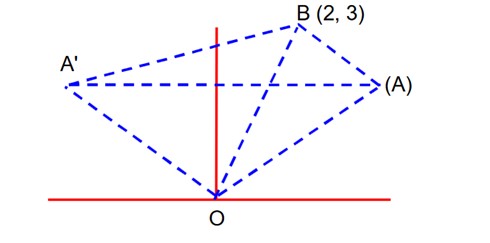
The distance between the two points A and A’ which lie on y = 2 such that both the line segments AB and A’B (where B is the point (2, 3)) subtend angle at the origin, is equal to:
Let A, A’ be (, 2) AB and A’B subtends angle at (0, 0) slope of OA =
slope of OB =
now distance between A’A, (10, 2) &
A wire of length 22m is to be cut into two pieces. One of the pieces is to be made into a square and the other into an equilateral triangle. Then, the length of the side of the equilateral triangle, so that the combined area of the square and the equilateral triangle is minimum, is:
Let perimeter of is x and that of square is 22 – x
now area
for maximum or minimum,
x
now side of a
The domain of the function
Case 1: 1
4x2 – 1
So x
If the constant term in the expansion of where is an odd integer, then the value of k is equal to:
General term
Now for constant term 3 + 2 …………..(i)
…………(ii)
From equation (i) & (ii)
= 1, = 3, = 6
Constant term
where [t] denotes greatest integer less than or equal to t, is equal to:
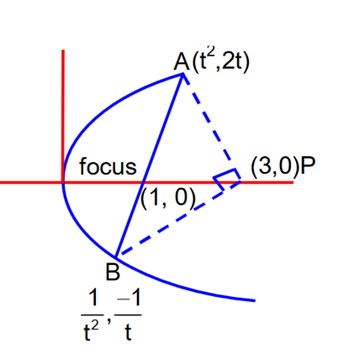
Let PQ be a focal chord of the parabola y2 = 4x such that it subtends an angle of at the point (3, 0). Let the line segment PQ be also a focal chord of the ellipse E: If e is the eccentricity of the ellipse E, then the value of is equal to:
M1 M2 = 1
t = 1
So, A (1, 2) and B (1, 2) they must be end pts of focal chord.
Length of latus rectum
b2 = 2a and ae = 1
Eccentricity of ellipse (Horizontal)
b2 = a2 (1 – e2)
2a = a2 (1 – e2)
2 =
e2 + 2e – 1 = 0
now
Let the tangent to the circle C1 : x2 + y2 = 2 at the point M(1, 1) intersect the circle + at two distinct points A and B. If the tangents to C2 at the points A and B intersect at N, then the area of the triangle ANB is equal to:
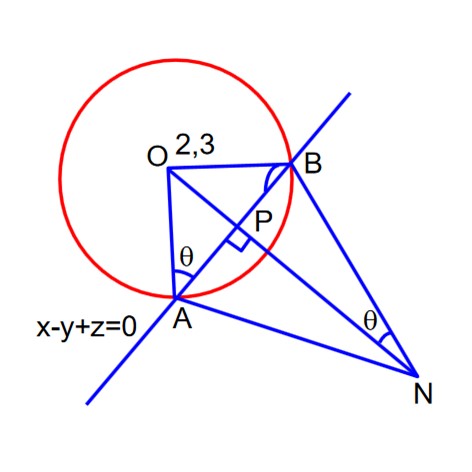
Tangent to C1 at (-1, 1) is T = 0
x(-1) + 4(1) = 2
-x + y = 2
find OP by dropping from (3, 2) to centre
OP =
AP =
area of
AN =
sin =
Let the mean and the variance of 5 observations respectively. If the mean and variance of the first 4 observation are and a respectively, then (4a + x5) is equal to:
and
x5 = 10
Variance
and
49 + 49 +
49
4a + 149 = 154
4a = 5
now 4a + x5 = 15
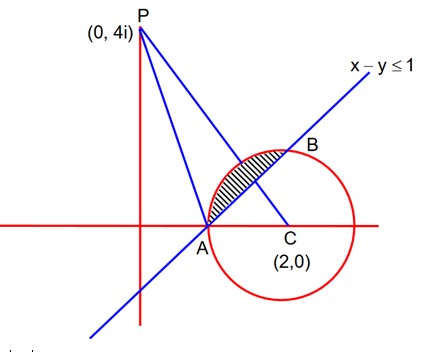
Let S = attains minimum and maximum values, respectively, at If where and are integers, then the value of + is equal to……………
Let z = x + iy
(x – 2)2 + y2
x – y
PD will be least as CP – r = DP, general pts on circle with centre (2, 0) is (2 + r cos, 0 + r sin )
here r = 1, (2 + cos , sin ) now slope of CP is
tan = 2
so D point will be will be the greatest. A(1, 0)
now
now
= 30, = 4
+ = 26
Let y = y(x) be the solution of the differential equation
2cos4 x – cos2x =
now IF =
Solution:
at
at
tan-1 a + tan-1
cot-1a = tan-1
tan-1
2 =
Let d be the distance between the foot of perpendiculars of the points P(1, 2, -1) and Q(2, -1, 3) on the plane -x + y + z = 1. Then d2 is equal to…………..
Let
1 2 > 0 as both pt.lies on same side
now
P2 =
as P1 = P2 so distance between foot of perpendicular will be same as distance between the points
d =
=
The number of elements in the set
is…………….
3cos22θ + 6cos2θ -
Þ cos2θ = 0,
Draw y = cos2θ, y = 0 and y = find the pt. of intersection.
The number of solutions of the equation 2θ - cos2θ + = 0 in R is equal to………..
Draw y = cos2x and y = 2x +
is equal to……………..
Let and for all x, y R, then the value of is equal to………….
f (x) = (c + 1)x2 + (1 – c2)x + 2k
Let be a hyperbola such that the sum of lengths of the transverse and the conjugate axes is If the eccentricity H is then the value of a2 + b2 is equal to………….
Given 2a + 2b =
4b2 = 7a2
b =
Let be a plane. Let P2 be another plane which passes through the points . If the direction ratios of the line of intersection of P1 and P2 be 16, , then the value of + is equal to……………
2x + y – 3z = 4
now line lying in both the planes have DR.
So direction ratio’s a : b : c = 16 : 13 : 15
f(0) = 0
c = 3/2
now
now
Let b1 b2 b3 b4 be a 4-element permutation with for such that either b1, b2, b3 are consecutive integers or b2, b3, b4 are consecutive integers. Then the number of such permutations b1 b2 b3 b4 is equal to……………
Three consecutive integers belong to 98 sets and four consecutive integers belongs to 97 sets.
Þ Number of permutations of b1 b2 b3 b4 = number of permutations when b1 b2 b3 are consecutive + number of permutations when b2, b3, b4 are consecutive – b1 b2 b3 b4 are consecutive = 98 * 97 * 98 * 97 – 97 = 18915
JEE Mains 2022
JEE Mains 2022
JEE Mains 2022
JEE Mains 2022
Commonly asked questions
Consider a matrix A = , where , , are three distinct natural numbers.
If then the number of such 3 – tuples (, , ) is…………
Kindly consider the following figure
The number of functions f, from the set A = to the set B = such that f(x) (x – 3)2 + 1, for every x A, is…………
A = {1, 2, 3, ……, 9}
for set B,
total number of such function = 2 × 1 × 1 × 1 × 2 × 3 × 4 × 5 × 6 = 2 × 6! = 1440
Let for the 9th term in the binomial expansion of , in the increasing powers of 6x, to be the greatest for x , the least value of n is n0. If k is the ratio of the coefficient of x6 to the coefficient of x3, then k + n0 is equal to:
Kindly consider the following figure
tn = n
A water tank has the shape of a right circular cone with axis vertical and vertex downwards. Its semi-vertical angle is Water is poured in it a constant rate of 6 cubic meter per hour. The rate (in square meter per hour), at which the wet curved surface area of the tank is increasing, when the depth of water in the tank is 4 meters, is………..
CSA =
For the curve C : the value of at the point (a, a), a > 0, on C, is equal to………..
Find a, α
zx differentiate the curve
……. (i)
differentiate equation (i)
Let f(x) = where [t] denotes the greatest integer t. Then is equal to………..
Use [x + n] = n + [x], where
Let f be a differentiable function satisfying f(x) = x > 0 and f(1) = . If y = f(x) passes through the point (a, 6), then a is equal to………….
Substitute
differentiate using leibneitz rule
f (1) =
A common tangent T to the curves and C2 = does not pass through the fourth quadrant. If T touches C1 at (x1, y1) and C2 at (x2, y2), then is equal to………
Common tangents
So, 4m2 + 9 = 42 m2 – 13 Þ m =
So tangent
y = 2x + 5 does not pass through 4th quadrant compare this tangent with T = 0 to get pt. of intersection
Let be three non-coplanar vectors such that and If then a is equal to…….
Data contradiction.
Maths NCERT Exemplar Solutions Class 12th Chapter Five Exam