Solve: (dydx)+xy=x(sinx+logx) .

This is a Long Answer Type Questions as classified in NCERT Exemplar Sol: T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s y + d d x ( x y ) = x ( s i n x + l o g x ) ⇒ y + x . d y d x + y = x ( s i n x + l o g x ) ⇒ x d y d x = x ( s i n x + l o g x ) − 2 y ⇒ d y d x = ( s i n x + l o g x ) − 2 y x ⇒ d y d x + 2 x y = ( s i n x + l o g x ) H e r e , P = 2 x a n d Q = ( s i n x + l o g x ) I n t e g r a t i n g f a c t o r I . F = e ∫ P d x = e ∫ 2 x . d x = e 2 l o g x = e l o g x 2 = x 2 ∴ S o l u t i o n o f t h e e q u a t i o n i s y × I . F . = ∫ Q × I . F . d x + c ⇒ y . x 2 = ∫ ( s i n x + l o g x ) x 2 d x + c … ( 1 ) L e t I = ∫ ( s i n x + l o g x ) x 2 d x = ∫ x 2 I s i n x I I d x + ∫ x 2 I I l o g x I d x = [ x 2 . ∫ s i n x d x − ∫ ( D ( x 2 ) . ∫ s i n x d x ) d x ] + [ l o g x . ∫ x 2 d x − ∫ ( D ( l o g x ) . ∫ x 2 d x ) d x ] = [ x 2 ( − c o s x ) − 2 ∫ − x c o s x d x ] + [ l o g x . x 3 3 − ∫ 1 x . x 3 3 d x ] = [ − x 2 c o s x + 2 ( x s i n x − ∫ 1 . s i n x d x ) ] + [ x 3 3 l o g x − 1 3 ∫ x 2 d x ] = − x 2 c o s x + 2 x s i n x + 2 c o s x + x 3 3 l o g x − 1 9 x 3 N o w f r o m e q ( 1 ) w e g e t , y . x 2 = − x 2 c o s x + 2 x s i n x + 2 c o s x + x 3 3 l o g x − 1 9 x 3 + c ∴ y = − c o s x + 2 s i n x x + 2 c o s x x 2 + x l o g x 3 − 1 9 x + c . x − 2 H e n c e , t h e r e q u i r e d s o l u t i o n i s y = − c o s x + 2 s i n x x + 2 c o s x x 2 + x l o g x 3 − 1 9 x + c . x − 2

Solve: dydx=cos(x+y)+sin(x+y) . [Hint: Substitute x+y=z ]

This is a Long Answer Type Questions as classified in NCERT Exemplar Sol: G i v e n t h a t d y d x = c o s ( x + y ) + s i n ( x + y ) P u t x + y = v , o n d i f f e r e n t i a t i n g w . r . t . x , w e g e t , 1 + d y d x = d v d x ∴ d y d x = d v d x − 1 ∴ d v d x − 1 = c o s v + s i n v ⇒ d v d x = c o s v + s i n v + 1 ⇒ d v c o s v + s i n v + 1 = d x I n t e g r a t i n g b o t h s i d e s , w e h a v e ∫ d v c o s v + s i n v + 1 = ∫ 1 . d x ⇒ ∫ d v ( 1 − t a n 2 v 2 1 + t a n 2 v 2 + 2 t a n v 2 1 + t a n 2 v 2 + 1 ) = ∫ 1 . d x ⇒ ∫ 1 + t a n 2 v 2 ( 1 − t a n 2 v 2 + 2 t a n v 2 + 1 ) d v = ∫ 1 . d x ⇒ ∫ s e c 2 v 2 2 + 2 t a n v 2 d v = ∫ 1 . d x P u t 2 + 2 t a n v 2 = t 2 . 1 2 s e c 2 v 2 d v = d t ⇒ s e c 2 v 2 d v = d t ⇒ ∫ d t 2 = ∫ 1 . d x ⇒ l o g | t | = x + c ⇒ l o g | 2 + 2 t a n v 2 | = x + c ⇒ l o g | 2 + 2 t a n ( x + y 2 ) | = x + c ⇒ l o g 2 [ 1 + t a n ( x + y 2 ) ] = x + c ⇒ l o g 2 + l o g [ 1 + t a n ( x + y 2 ) ] = x + c ⇒ l o g [ 1 + t a n ( x + y 2 ) ] = x + c − l o g 2 H e n c e , t h e r e q u i r e d s o l u t i o n i s l o g [ 1 + t a n ( x + y 2 ) ] = x + K [ c − l o g 2 = K ]

Find the general solution of dydx−3y=sin 2x

This is a Long Answer Type Questions as classified in NCERT Exemplar Sol: G i v e n e q u a t i o n i s d y d x − 3 y = s i n 2 x H e r e , P = − 3 a n d Q = s i n 2 x I n t e g r a t i n g f a c t o r I . F = e ∫ P d x = e ∫ − 3 . d x = e − 3 x ∴ S o l u t i o n o f t h e e q u a t i o n i s y × I . F . = ∫ Q × I . F . d x + c ⇒ y . e − 3 x = ∫ s i n 2 x . e − 3 x d x + c L e t I = ∫ s i n 2 x I . e − 3 x I I d x ⇒ I = s i n 2 x . ∫ e − 3 x d x − ∫ ( D ( s i n 2 x ) . ∫ e − 3 x d x ) d x ⇒ I = s i n 2 x . e − 3 x − 3 − ∫ 2 c o s 2 x . e − 3 x − 3 d x ⇒ I = e − 3 x − 3 s i n 2 x + 2 3 ∫ c o s 2 x I . e − 3 x I I d x ⇒ I = e − 3 x − 3 s i n 2 x + 2 3 [ c o s 2 x . ∫ e − 3 x d x − ∫ ( D ( c o s 2 x ) . ∫ e − 3 x d x ) d x ] ⇒ I = e − 3 x − 3 s i n 2 x + 2 3 [ c o s 2 x . e − 3 x − 3 − ∫ 2 s i n 2 x . e − 3 x − 3 d x ] ⇒ I = e − 3 x − 3 s i n 2 x − 2 9 c o s 2 x . e − 3 x − 4 9 ∫ s i n 2 x . e − 3 x d x ⇒ I = e − 3 x − 3 s i n 2 x − 2 9 c o s 2 x . e − 3 x − 4 9 I ⇒ I + 4 9 I = e − 3 x − 3 s i n 2 x − 2 9 e − 3 x c o s 2 x ⇒ 1 3 9 I = − 1 9 [ 3 e − 3 x s i n 2 x + 2 e − 3 x c o s 2 x ] ⇒ I = − 1 1 3 e − 3 x [ 3 s i n 2 x + 2 c o s 2 x ] ∴ T h e e q u a t i o n b e c o m e s ⇒ y . e − 3 x = − 1 1 3 e − 3 x [ 3 s i n 2 x + 2 c o s 2 x ] + c ∴ y = − 1 1 3 [ 3 s i n 2 x + 2 c o s 2 x ] + c . e 3 x H e n c e , t h e r e q u i r e d s o l u t i o n i s y = − [ 3 s i n 2 x + 2 c o s 2 x 1 3 ] + c . e 3 x

Let R be a relation from the set {1,2,3,.....,60} to itself such that R = {(a,b):b=pq} where p, q ≥ 3 are prime numbers. Then, the number of elements in R is:

R = { (a, b): b = pq, where p, q ≥3 are prime} ⇒60×11=660 p, q ∈ {3, 5, 7, 11, 13, 17, 19, 23, 29, 3, 37, 41, 43, 47, 53, 59} total 16 p, q ∈ {3, 5, 7, 11, 13, 17, 19} {3, 5, 7, 11, 13, 17, 19} 7 + 3 + 1 = 11

If z = 2 + 3 i, then z5 + (z¯)5 is equal to:

z5+ (z¯)5 = (2+3i)5+ (2−3i)5 =2 (32−720+810)=244

1(20−a)(40−a)+1(40−a)(60−a)+...+1(180−a)(200−a)=1256, then the maximum value of a is:

1(20−a)(40−a)+1(40−a)(60−a)+1(60−a)(80−a)+.....+1(180−a)(200−a)=1256 LHS = 120(120−a−140−a)+120(140−a−160−a)+...+120(1180−a−1200−a) =120(120−a−1200−a)=120.180(20−a)(200−a) ⇒a2−220a+4000−2304=0⇒a2220a+1696=0 a=220±2048=2122

If limx→0αex+βe−x+γsinxxsin2x=23, where α,β,γ∈R, then which of the following is NOT correct?

limx→0αex+βe−x+γsinxxsin2x =limx→0αex+βe−x+γsinxx3 ⇒α+β=0, α−β+γ=0, α+β2=0, α6−β6−γ6=23 ⇒β=−αγ=−2αα−β−γ=4⇒α+α+2α=4⇒γ=1 α=1, β=−1, γ=−2

Maths NCERT Exemplar Solutions Class 12th Chapter Nine: Overview, Questions, Preparation

Q: Let A and B be two 3 × 3 non-zero real matrices such that AB is a zero matrix. Then

A3×3, B3×3&AB=0 ≠0≠0⇒|A|=0 &|B|=0 only .

Updated on Jul 11, 2025 15:09 IST

By Vishal Baghel, Executive Content Operations

Table of content

Differential Equations Questions and Answers
JEE Mains Solution 2022

Differential Equations Questions and Answers

Q1.Solve: $(\frac{d y}{d x}) + x y = x (s i n x + l o g x)$ .

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s y + \frac{d}{d x} (x y) = x (s i n x + l o g x) \\ \Rightarrow y + x . \frac{d y}{d x} + y = x (s i n x + l o g x) \\ \Rightarrow x \frac{d y}{d x} = x (s i n x + l o g x) - 2 y \\ \Rightarrow \frac{d y}{d x} = (s i n x + l o g x) - \frac{2 y}{x} \\ \Rightarrow \frac{d y}{d x} + \frac{2}{x} y = (s i n x + l o g x) \\ H e r e, P = \frac{2}{x} a n d Q = (s i n x + l o g x) \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int \frac{2}{x} . d x} = e^{2 l o g x} = e^{l o g x^{2}} = x^{2} \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y . x^{2} = \int (s i n x + l o g x) x^{2} d x + c \dots (1) \\ L e t I = \int (s i n x + l o g x) x^{2} d x \\ = \int \underset{I}{x^{2}} \underset{I I}{s i n x} d x + \int \underset{I I}{x^{2}} \underset{I}{l o g x} d x \\ = [x^{2} . \int s i n x d x - \int (D (x^{2}) . \int s i n x d x) d x] + [l o g x . \int x^{2} d x - \int (D (l o g x) . \int x^{2} d x) d x] \\ = [x^{2} (- c o s x) - 2 \int - x c o s x d x] + [l o g x . \frac{x^{3}}{3} - \int \frac{1}{x} . \frac{x^{3}}{3} d x] \\ = [- x^{2} c o s x + 2 (x s i n x - \int 1 . s i n x d x)] + [\frac{x^{3}}{3} l o g x - \frac{1}{3} \int x^{2} d x] \\ = - x^{2} c o s x + 2 x s i n x + 2 c o s x + \frac{x^{3}}{3} l o g x - \frac{1}{9} x^{3} \\ N o w f r o m e q (1) w e g e t, \\ y . x^{2} = - x^{2} c o s x + 2 x s i n x + 2 c o s x + \frac{x^{3}}{3} l o g x - \frac{1}{9} x^{3} + c \\ ∴ y = - c o s x + \frac{2 s i n x}{x} + \frac{2 c o s x}{x^{2}} + \frac{x l o g x}{3} - \frac{1}{9} x + c . x^{- 2} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s \\ y = - c o s x + \frac{2 s i n x}{x} + \frac{2 c o s x}{x^{2}} + \frac{x l o g x}{3} - \frac{1}{9} x + c . x^{- 2} \end{array}$

Q2.Find the general solution of $(1 + t a n y) (d x- d y) + 2 x d y = 0$ .

Sol:

$\begin{array}{l} G i v e n t h a t (1 + t a n y) (d x - d y) + 2 x d y = 0 \\ \Rightarrow (1 + t a n y) d x - (1 + t a n y) d y + 2 x d y = 0 \\ \Rightarrow (1 + t a n y) d x - (1 + t a n y - 2 x) d y = 0 \\ \Rightarrow (1 + t a n y) \frac{d x}{d y} = (1 + t a n y - 2 x) \Rightarrow \frac{d x}{d y} = \frac{1 + t a n y - 2 x}{1 + t a n y} \\ \Rightarrow \frac{d x}{d y} = 1 - \frac{2 x}{1 + t a n y} \Rightarrow \frac{d x}{d y} + \frac{2 x}{1 + t a n y} = 1 \\ H e r e, P = \frac{2}{1 + t a n y} a n d Q = 1 \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d y} = e^{\int \frac{2}{1 + t a n y} . d y} = e^{\int \frac{2 c o s y}{s i n y + c o s y} . d y} \\ = e^{\int \frac{s i n y + c o s y - s i n y + c o s y}{s i n y + c o s y} . d y} = e^{\int (1 + \frac{c o s y - s i n y}{s i n y + c o s y}) . d y} \\ = e^{\int 1 . d y} . e^{\int \frac{c o s y - s i n y}{s i n y + c o s y} . d y} = e^{y} . e^{l o g (s i n y + c o s y)} = e^{y} . (s i n y + c o s y) \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ x \times I . F . = \int Q \times I . F . d y + c \\ \Rightarrow x . e^{y} . (s i n y + c o s y) = \int 1 . e^{y} . (s i n y + c o s y) d y + c \\ \Rightarrow x . e^{y} . (s i n y + c o s y) = e^{y} . s i n y + c [∵ \int e^{x} [f (x) + f^{'} (x)] d x = e^{x} f (x) + c] \\ \Rightarrow x (s i n y + c o s y) = s i n y + c . e^{- y} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s x (s i n y + c o s y) = s i n y + c . e^{- y} \end{array}$

Q3.Solve: $\frac{d y}{d x} = c o s (x + y) + s i n (x + y)$ . [Hint: Substitute $x + y = z$ ]

Sol:

$\begin{array}{l} G i v e n t h a t \frac{d y}{d x} = c o s (x + y) + s i n (x + y) \\ P u t x + y = v, o n d i f f e r e n t i a t i n g w . r . t . x, w e g e t, \\ 1 + \frac{d y}{d x} = \frac{d v}{d x} \\ ∴ \frac{d y}{d x} = \frac{d v}{d x} - 1 \\ ∴ \frac{d v}{d x} - 1 = c o s v + s i n v \\ \Rightarrow \frac{d v}{d x} = c o s v + s i n v + 1 \\ \Rightarrow \frac{d v}{c o s v + s i n v + 1} = d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int \frac{d v}{c o s v + s i n v + 1} = \int 1 . d x \\ \Rightarrow \int \frac{d v}{(\frac{1 - t a n^{2} \frac{v}{2}}{1 + t a n^{2} \frac{v}{2}} + \frac{2 t a n \frac{v}{2}}{1 + t a n^{2} \frac{v}{2}} + 1)} = \int 1 . d x \\ \Rightarrow \int \frac{1 + t a n^{2} \frac{v}{2}}{(1 - t a n^{2} \frac{v}{2} + 2 t a n \frac{v}{2} + 1)} d v = \int 1 . d x \\ \Rightarrow \int \frac{s e c^{2} \frac{v}{2}}{2 + 2 t a n \frac{v}{2}} d v = \int 1 . d x \\ P u t 2 + 2 t a n \frac{v}{2} = t \\ 2 . \frac{1}{2} s e c^{2} \frac{v}{2} d v = d t \Rightarrow s e c^{2} \frac{v}{2} d v = d t \\ \Rightarrow \int \frac{d t}{2} = \int 1 . d x \\ \Rightarrow l o g | t | = x + c \\ \Rightarrow l o g | 2 + 2 t a n \frac{v}{2} | = x + c \\ \Rightarrow l o g | 2 + 2 t a n (\frac{x + y}{2}) | = x + c \\ \Rightarrow l o g 2 [1 + t a n (\frac{x + y}{2})] = x + c \\ \Rightarrow l o g 2 + l o g [1 + t a n (\frac{x + y}{2})] = x + c \\ \Rightarrow l o g [1 + t a n (\frac{x + y}{2})] = x + c - l o g 2 \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s l o g [1 + t a n (\frac{x + y}{2})] = x + K [c - l o g 2 = K] \end{array}$

Q4.Find the general solution of $\frac{d y}{d x} - 3 y = s i n 2 x$ .

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s \frac{d y}{d x} - 3 y = s i n 2 x \\ H e r e, P = - 3 a n d Q = s i n 2 x \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int - 3 . d x} = e^{- 3 x} \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y . e^{- 3 x} = \int s i n 2 x . e^{- 3 x} d x + c \\ L e t I = \int \underset{I}{s i n 2 x} . \underset{I I}{e^{- 3 x}} d x \\ \Rightarrow I = s i n 2 x . \int e^{- 3 x} d x - \int (D (s i n 2 x) . \int e^{- 3 x} d x) d x \\ \Rightarrow I = s i n 2 x . \frac{e^{- 3 x}}{- 3} - \int 2 c o s 2 x . \frac{e^{- 3 x}}{- 3} d x \\ \Rightarrow I = \frac{e^{- 3 x}}{- 3} s i n 2 x + \frac{2}{3} \int \underset{I}{c o s 2 x} . \underset{I I}{e^{- 3 x}} d x \\ \Rightarrow I = \frac{e^{- 3 x}}{- 3} s i n 2 x + \frac{2}{3} [c o s 2 x . \int e^{- 3 x} d x - \int (D (c o s 2 x) . \int e^{- 3 x} d x) d x] \\ \Rightarrow I = \frac{e^{- 3 x}}{- 3} s i n 2 x + \frac{2}{3} [c o s 2 x . \frac{e^{- 3 x}}{- 3} - \int 2 s i n 2 x . \frac{e^{- 3 x}}{- 3} d x] \\ \Rightarrow I = \frac{e^{- 3 x}}{- 3} s i n 2 x - \frac{2}{9} c o s 2 x . e^{- 3 x} - \frac{4}{9} \int s i n 2 x . e^{- 3 x} d x \\ \Rightarrow I = \frac{e^{- 3 x}}{- 3} s i n 2 x - \frac{2}{9} c o s 2 x . e^{- 3 x} - \frac{4}{9} I \\ \Rightarrow I + \frac{4}{9} I = \frac{e^{- 3 x}}{- 3} s i n 2 x - \frac{2}{9} e^{- 3 x} c o s 2 x \\ \Rightarrow \frac{13}{9} I = - \frac{1}{9} [3 e^{- 3 x} s i n 2 x + 2 e^{- 3 x} c o s 2 x] \\ \Rightarrow I = - \frac{1}{13} e^{- 3 x} [3 s i n 2 x + 2 c o s 2 x] \\ ∴ T h e e q u a t i o n b e c o m e s \\ \Rightarrow y . e^{- 3 x} = - \frac{1}{13} e^{- 3 x} [3 s i n 2 x + 2 c o s 2 x] + c \\ ∴ y = - \frac{1}{13} [3 s i n 2 x + 2 c o s 2 x] + c . e^{3 x} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s y = - [\frac{3 s i n 2 x + 2 c o s 2 x}{13}] + c . e^{3 x} \end{array}$

Commonly asked questions

Solve: $(\frac{d y}{d x}) + x y = x (s i n x + l o g x)$ .

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

Find the general solution of $(1 + t a n y) (d x- d y) + 2 x d y = 0$ .

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t (1 + t a n y) (d x - d y) + 2 x d y = 0 \\ \Rightarrow (1 + t a n y) d x - (1 + t a n y) d y + 2 x d y = 0 \\ \Rightarrow (1 + t a n y) d x - (1 + t a n y - 2 x) d y = 0 \\ \Rightarrow (1 + t a n y) \frac{d x}{d y} = (1 + t a n y - 2 x) \Rightarrow \frac{d x}{d y} = \frac{1 + t a n y - 2 x}{1 + t a n y} \\ \Rightarrow \frac{d x}{d y} = 1 - \frac{2 x}{1 + t a n y} \Rightarrow \frac{d x}{d y} + \frac{2 x}{1 + t a n y} = 1 \\ H e r e, P = \frac{2}{1 + t a n y} a n d Q = 1 \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d y} = e^{\int \frac{2}{1 + t a n y} . d y} = e^{\int \frac{2 c o s y}{s i n y + c o s y} . d y} \\ = e^{\int \frac{s i n y + c o s y - s i n y + c o s y}{s i n y + c o s y} . d y} = e^{\int (1 + \frac{c o s y - s i n y}{s i n y + c o s y}) . d y} \\ = e^{\int 1 . d y} . e^{\int \frac{c o s y - s i n y}{s i n y + c o s y} . d y} = e^{y} . e^{l o g (s i n y + c o s y)} = e^{y} . (s i n y + c o s y) \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ x \times I . F . = \int Q \times I . F . d y + c \\ \Rightarrow x . e^{y} . (s i n y + c o s y) = \int 1 . e^{y} . (s i n y + c o s y) d y + c \\ \Rightarrow x . e^{y} . (s i n y + c o s y) = e^{y} . s i n y + c [? \int e^{x} [f (x) + f^{'} (x)] d x = e^{x} f (x) + c] \\ \Rightarrow x (s i n y + c o s y) = s i n y + c . e^{- y} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s x (s i n y + c o s y) = s i n y + c . e^{- y} \end{array}$

Solve: $\frac{d y}{d x} = c o s (x + y) + s i n (x + y)$ . [Hint: Substitute $x + y = z$ ]

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

Find the general solution of $\frac{d y}{d x} - 3 y = s i n 2 x$

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

Find the equation of a curve passing through $(2, 1)$ if the slope of the tangent to the curve at any point $(x, y)$ is $\frac{x^{2} + y^{2}}{2 x y} .$

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t t h e s l o p e o f tangent t o a c u r v e a t (x, y) i s \\ \frac{d y}{d x} = \frac{x^{2} + y^{2}}{2 x y} \\ I t i s a homogeneous d i f f e r e n t i a l e q u a t i o n \\ S o, p u t y = v x \Rightarrow \frac{d y}{d x} = v + x . \frac{d v}{d x} \\ \Rightarrow v + x . \frac{d v}{d x} = \frac{x^{2} + v^{2} x^{2}}{2 x . v x} \\ \Rightarrow v + x . \frac{d v}{d x} = \frac{1 + v^{2}}{2 v} \\ \Rightarrow x . \frac{d v}{d x} = \frac{1 + v^{2}}{2 v} - v \Rightarrow x . \frac{d v}{d x} = \frac{1 + v^{2} - 2 v^{2}}{2 v} \\ \Rightarrow x . \frac{d v}{d x} = \frac{1 - v^{2}}{2 v} \Rightarrow \frac{2 v}{1 - v^{2}} d v = \frac{d x}{x} \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int \frac{2 v}{1 - v^{2}} d v = \int \frac{d x}{x} \\ \Rightarrow - l o g | 1 - v^{2} | = l o g x + l o g c \\ \Rightarrow - l o g | 1 - \frac{y^{2}}{x^{2}} | = l o g x + l o g c \Rightarrow - l o g | \frac{x^{2} - y^{2}}{x^{2}} | = l o g x + l o g c \\ \Rightarrow l o g | \frac{x^{2}}{x^{2} - y^{2}} | = l o g | x c | \Rightarrow \frac{x^{2}}{x^{2} - y^{2}} = x c \\ Since, t h e c u r v e i s passing t h r o u g h t h e point (2, 1) \\ ∴ \frac{{(2)}^{2}}{{(2)}^{2} - {(1)}^{2}} = 2 c \Rightarrow \frac{4}{3} = 2 c \Rightarrow c = \frac{2}{3} \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s \frac{x^{2}}{x^{2} - y^{2}} = \frac{2}{3} x \Rightarrow 2 (x^{2} - y^{2}) = 3 x \end{array}$

Find the equation of the curve through the point $(1, 0)$ if the slope of the tangent to the curve at any point $(x, y)$ is $\frac{y - 1}{x (x + 2)} .$

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t t h e s l o p e o f tangent t o a c u r v e a t (x, y) i s \\ \frac{d y}{d x} = \frac{y - 1}{x^{2} + x} \Rightarrow \frac{d y}{y - 1} = \frac{d x}{x^{2} + x} \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int \frac{d y}{y - 1} = \int \frac{d x}{x^{2} + x} \\ \Rightarrow \int \frac{d y}{y - 1} = \int \frac{d x}{x^{2} + x + \frac{1}{4} - \frac{1}{4}} [M a k i n g p e r f e c t s q u a r e] \\ \Rightarrow \int \frac{d y}{y - 1} = \int \frac{d x}{{(x + \frac{1}{2})}^{2} - {(\frac{1}{2})}^{2}} \\ \Rightarrow l o g | y - 1 | = \frac{1}{2 \times \frac{1}{2}} l o g | \frac{x + \frac{1}{2} - \frac{1}{2}}{x + \frac{1}{2} + \frac{1}{2}} | + l o g c \\ \Rightarrow l o g | y - 1 | = l o g | \frac{x}{x + 1} | + l o g c \\ \Rightarrow l o g | y - 1 | = l o g | c (\frac{x}{x + 1}) | \\ ∴ y - 1 = \frac{c x}{x + 1} \Rightarrow (y - 1) (x + 1) = c x \\ Since, t h e l i n e i s passing t h r o u g h t h e point (1, 0), t h e n \\ (0 - 1) (1 + 1) = c (1) \Rightarrow c = 2 \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s (y - 1) (x + 1) = 2 x . \end{array}$

Find the equation of a curve passing through the origin if the slope of the tangent to the curve at any point $(x, y)$ is equal to the square of the difference of the abscissa and ordinate of the point.

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} H e r e, s l o p e o f t h e o f t h e c u r v e = \frac{d y}{d x} \\ a n d t h e d i f f e r e n c e b e t w e e n t h e a b s c i s s a a n d o r d i n a t e = x - y . \\ ∴ A s p e r t h e c o n d i t i o n, \frac{d y}{d x} = {(x - y)}^{2} \\ P u t x - y = v \\ 1 - \frac{d y}{d x} = \frac{d v}{d x} \\ ∴ \frac{d y}{d x} = 1 - \frac{d v}{d x} \\ ∴ t h e e q u a t i o n b e c o m e s \\ 1 - \frac{d v}{d x} = v^{2} \Rightarrow \frac{d v}{d x} = 1 - v^{2} \Rightarrow \frac{d v}{1 - v^{2}} = d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{d v}{1 - v^{2}} = \int d x \\ \Rightarrow \frac{1}{2} l o g | \frac{1 + v}{1 - v} | = x + c \Rightarrow \frac{1}{2} l o g | \frac{1 + x - y}{1 - x + y} | = x + c \dots (1) \\ Since, t h e c u r v e i s t h r o u g h (0, 0), t h e n \\ \Rightarrow \frac{1}{2} l o g | \frac{1 + 0 - 0}{1 - 0 + 0} | = 0 + c \Rightarrow c = 0 \\ ∴ O n p u t t i n g c = 0 i n e q . (1) w e g e t \\ \frac{1}{2} l o g | \frac{1 + x - y}{1 - x + y} | = x \Rightarrow l o g | \frac{1 + x - y}{1 - x + y} | = 2 x \\ ∴ \frac{1 + x - y}{1 - x + y} = e^{2 x} \\ \Rightarrow (1 + x - y) = e^{2 x} (1 - x + y) \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s (1 + x - y) = e^{2 x} (1 - x + y) . \end{array}$

Find the equation of a curve passing through the point $(1, 1)$ . If the tangent drawn at any point $P (x, y)$ on the curve meets the coordinate axes at $A$ and $B$ such that $P$ is the midpoint of $A B$ .

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

Solve: $x \frac{d y}{d x} = y (l o g y - l o g x + 1) .$

This is a Long Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n t h a t x \frac{d y}{d x} = y (l o g y - l o g x + 1) \\ \Rightarrow x \frac{d y}{d x} = y [l o g (\frac{y}{x}) + 1] \\ \Rightarrow \frac{d y}{d x} = \frac{y}{x} [l o g (\frac{y}{x}) + 1] \\ Since, i t i s a d i f f e r e n t i a l e q u a t i o n \\ S o, p u t y = v x \Rightarrow \frac{d y}{d x} = v + x . \frac{d v}{d x} \\ \Rightarrow v + x . \frac{d v}{d x} = \frac{v x}{x} [l o g (\frac{v x}{x}) + 1] \\ \Rightarrow v + x . \frac{d v}{d x} = v [l o g v + 1] \\ \Rightarrow x . \frac{d v}{d x} = v [l o g v + 1] - v \Rightarrow x . \frac{d v}{d x} = v [l o g v + 1 - 1] \\ \Rightarrow x . \frac{d v}{d x} = v . l o g v \Rightarrow \frac{d v}{v l o g v} = \frac{d x}{x} \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int \frac{d v}{v l o g v} = \int \frac{d x}{x} \\ P u t l o g v = t o n L . H . S . \\ \Rightarrow \frac{1}{v} d v = d t \\ ∴ \int \frac{d t}{t} = \int \frac{d x}{x} \\ \Rightarrow l o g | t | = l o g | x | + l o g c \\ \Rightarrow l o g | l o g v | = l o g x c \Rightarrow l o g v = x c \\ \Rightarrow l o g (\frac{y}{x}) = x c \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s l o g (\frac{y}{x}) = x c . \end{array}$

Find the solution of $\frac{d y}{d x} = 2^{y - x}$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} = 2^{y - x} \Rightarrow \frac{d y}{d x} = \frac{2^{y}}{2^{x}} \\ S e p a r a t i n g t h e v a r i a b l e s, w e g e t \\ \frac{d y}{2^{y}} = \frac{d x}{2^{x}} \Rightarrow 2^{- y} d y = 2^{- x} d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int 2^{- y} d y = \int 2^{- x} d x \\ \frac{- 2^{- y}}{l o g 2} = \frac{- 2^{- x}}{l o g 2} + c \Rightarrow - 2^{- y} = - 2^{- x} + c l o g 2 \\ \Rightarrow - 2^{- y} + 2^{- x} = c l o g 2 \\ \Rightarrow 2^{- x} - 2^{- y} = k [w h e r e c l o g 2 = k] \end{array}$

Find the differential equation of all non-vertical lines in a plane.

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} E q u a t i o n o f a l l n o n v e r t i c a l l i n e s a r e y = m x + c \\ D i f f e r e n t i a t i n g w i t h r e s p e c t t o x, w e g e t \frac{d y}{d x} = m \\ A g a i n d i f f e r e n t i a t i n g w . r . t . x w e h a v e \frac{d^{2} y}{d x^{2}} = 0 \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s \frac{d^{2} y}{d x^{2}} = 0 . \end{array}$

Given that $\frac{d y}{d x} = e^{- 2 y}$ and $y = 0$ when $x = 5$ . Find the value of $x$ when $y = 3$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s \frac{d y}{d x} = e^{- 2 y} \\ \Rightarrow \frac{d y}{e^{- 2 y}} = d x \Rightarrow e^{2 y} . d y = d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int e^{2 y} . d y = \int d x \Rightarrow \frac{1}{2} e^{2 y} = x + c \\ P u t y = 0 a n d x = 5 \\ \Rightarrow \frac{1}{2} e^{2 y} = 5 + c \Rightarrow c = \frac{1}{2} - 5 = - \frac{9}{2} \\ ∴ T h e e q u a t i o n b e c o m e s \frac{1}{2} e^{2 y} = x - \frac{9}{2} \\ N o w p u t t i n g y = 3, w e g e t \\ \frac{1}{2} e^{6} = x - \frac{9}{2} \Rightarrow x = \frac{1}{2} e^{6} + \frac{9}{2} \\ H e n c e, t h e r e q u i r e d v a l u e o f x = \frac{1}{2} (e^{6} + 9) . \end{array}$

Solve the differential equation $(x^{2} - 1) \frac{d y}{d x} + 2 x y = \frac{1}{x^{2} - 1}$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s (x^{2} - 1) \frac{d y}{d x} + 2 x y = \frac{1}{x^{2} - 1} \\ D i v i n d i n g b y (x^{2} - 1), w e g e t \\ \frac{d y}{d x} + \frac{x y}{x^{2} - 1} \Rightarrow \frac{1}{{(x^{2} - 1)}^{2}} \\ I t i s a l i n e a r d i f f e r e n t i a l e q u a t i o n o f f i r s t o r d e r a n d f i r s t degree . \\ ∴ P = \frac{2 x}{x^{2} - 1} a n d Q = \frac{1}{{(x^{2} - 1)}^{2}} \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int \frac{2 x}{x^{2} - 1} d x} = e^{l o g (x^{2} - 1)} = (x^{2} - 1) \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q . I . F . d x + c \\ \Rightarrow y (x^{2} - 1) = \int \frac{1}{x^{2} - 1} d x + c \Rightarrow y (x^{2} - 1) = \frac{1}{2} l o g | \frac{x - 1}{x + 1} | + c \\ H e n c e, t h e r e q u i r e d v a l u e i s y (x^{2} - 1) = \frac{1}{2} l o g | \frac{x - 1}{x + 1} | + c . \end{array}$

Solve the differential equation $\frac{d y}{d x} + 2 x y = y$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s \frac{d y}{d x} + 2 x y = y \\ \Rightarrow \frac{d y}{d x} = y - 2 x y \Rightarrow \frac{d y}{d x} = y (1 - 2 x) \Rightarrow \frac{d y}{y} = (1 - 2 x) d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ \int \frac{d y}{y} = \int (1 - 2 x) d x \Rightarrow l o g y = x - 2 . \frac{x^{2}}{2} + c \\ \Rightarrow l o g y = x - x^{2} + l o g c \Rightarrow l o g y - l o g c = x - x^{2} \\ \Rightarrow l o g \frac{y}{c} = x - x^{2} \Rightarrow \frac{y}{c} = e^{x - x^{2}} \\ ∴ y = c . e^{x - x^{2}} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s y = c . e^{x - x^{2}} . \end{array}$

Find the general solution of $\frac{d y}{d x} + a y = e^{m x}$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \frac{d y}{d x} + a y = e^{m x} \\ ∴ P = a a n d Q = e^{m x} \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int a . d x} = e^{a x} \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q . I . F . d x + c \\ \Rightarrow y . e^{a x} = \int e^{m x} . e^{a x} d x + c \Rightarrow y . e^{a x} = \int e^{(m + a) x} d x + c \\ \Rightarrow y . e^{a x} = \frac{e^{(m + a) x}}{(m + a)} + c \Rightarrow y = \frac{e^{(m + a) x}}{(m + a)} . e^{- a x} + c . e^{- a x} \\ ∴ y = \frac{e^{m x}}{(m + a)} + c . e^{- a x} \\ H e n c e, t h e r e q u i r e d v a l u e i s y = \frac{e^{m x}}{(m + a)} + c . e^{- a x} . \end{array}$

Solve the differential equation $\frac{d y}{d x} + 1 + y = e^{x + y}$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s \frac{d y}{d x} + 1 = e^{x + y} \\ P u t x + y = t \\ ∴ 1 + \frac{d y}{d x} = \frac{d t}{d x} \\ ∴ \frac{d t}{d x} = e^{t} \Rightarrow \frac{d t}{e^{t}} = d x \Rightarrow e^{- t} d t = d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int e^{- t} d t = \int d x \Rightarrow - e^{- t} = x + c \\ - e^{- (x + y)} = x + c \Rightarrow \frac{- 1}{e^{(x + y)}} x + c \Rightarrow (x + c) . e^{(x + y)} = - 1 \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s (x + c) . e^{(x + y)} + 1 = 0 . \end{array}$

Solve: $y d x - x d y = x^{2} y d x$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s y d x - x d y = x^{2} y d x \\ \Rightarrow y d x - x^{2} y d x = x d y \\ \Rightarrow y (1 - x^{2}) d x = x d y \\ \Rightarrow (\frac{1 - x^{2}}{x}) d x = \frac{d y}{y} \Rightarrow (\frac{1}{x} - x) d x = \frac{d y}{y} \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int (\frac{1}{x} - x) d x = \int \frac{d y}{y} \Rightarrow l o g x - \frac{x^{2}}{2} = l o g y + l o g c \\ \Rightarrow l o g x - \frac{x^{2}}{2} = l o g y c \Rightarrow l o g x - l o g y c = \frac{x^{2}}{2} \\ \Rightarrow l o g \frac{x}{y c} = \frac{x^{2}}{2} \Rightarrow \frac{x}{y c} = e^{\frac{x^{2}}{2}} \Rightarrow \frac{y c}{x} = e^{\frac{- x^{2}}{2}} \\ \Rightarrow y c = x e^{\frac{- x^{2}}{2}} \Rightarrow y = \frac{1}{c} . x e^{\frac{- x^{2}}{2}} \Rightarrow y = k x e^{\frac{- x^{2}}{2}} [? k = \frac{1}{c}] \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s k x e^{\frac{- x^{2}}{2}} . \end{array}$

Solve the differential equation $\frac{d y}{d x} = 1 + x + y^{2} + x y^{2}$ , when $y = 0$ , $x = 0$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s \frac{d y}{d x} = 1 + x + y^{2} + x y^{2} \\ \Rightarrow \frac{d y}{d x} = 1 (1 + x) + y^{2} (1 + x) \\ \Rightarrow \frac{d y}{d x} = (1 + x) (1 + y^{2}) \Rightarrow \frac{d y}{1 + y^{2}} \Rightarrow (1 + x) d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{d y}{1 + y^{2}} = \int (1 + x) d x \Rightarrow t a n^{- 1} y = x + \frac{x^{2}}{2} + c \\ P u t x = 0 a n d y = 0, w e g e t t a n^{- 1} (0) = 0 + 0 + c \Rightarrow c = 0 \\ ∴ t a n^{- 1} y = x + \frac{x^{2}}{2} y = t a n (x + \frac{x^{2}}{2}) \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s y = t a n (x + \frac{x^{2}}{2}) . \end{array}$

Find the general solution of $(x + 2 y^{3}) \frac{d y}{d x} = y$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s (x + 2 y^{3}) \frac{d y}{d x} = y \\ \Rightarrow \frac{d y}{d x} = \frac{y}{x + 2 y^{3}} \Rightarrow \frac{d x}{d y} = \frac{x + 2 y^{3}}{y} \\ \Rightarrow \frac{d x}{d y} = \frac{x}{y} + \frac{2 y^{3}}{y} \Rightarrow \frac{d x}{d y} - \frac{x}{y} = 2 y^{2} \\ ∴ P = - \frac{1}{y} a n d Q = 2 y^{2} \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int - \frac{1}{y} . d x} = e^{- l o g y} = e^{l o g \frac{1}{y}} = \frac{1}{y} \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ x \times I . F . = \int Q . I . F . d y + c \\ \Rightarrow x . \frac{1}{y} = \int 2 y^{2} . \frac{1}{y} d y + c \Rightarrow \frac{x}{y} = 2 \int y d y + c \\ \Rightarrow \frac{x}{y} = 2 . \frac{y^{2}}{2} + c \Rightarrow \frac{x}{y} = y^{2} + c \\ ∴ x = y^{3} + c y = y (y^{2} + c) \\ H e n c e, t h e r e q u i r e d v a l u e i s x = y (y^{2} + c) . \end{array}$

If $y (x)$ is a solution of $(\frac{2 + s i n x}{1 + y}) \frac{d y}{d x} + y = - c o s x$ and $y (0) = 1$ , then find the value of $y (\frac{π}{2})$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s (\frac{2 + s i n x}{1 + y}) \frac{d y}{d x} = - c o s x \\ \Rightarrow (\frac{2 + s i n x}{c o s x}) \frac{d y}{d x} = - (1 + y) \Rightarrow \frac{d y}{(1 + y)} = - (\frac{c o s x}{2 + s i n x}) d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{d y}{(1 + y)} = - \int (\frac{c o s x}{2 + s i n x}) d x \\ \Rightarrow l o g | 1 + y | = - l o g | 2 + s i n x | + l o g c \\ \Rightarrow l o g | 1 + y | + l o g | 2 + s i n x | = l o g c \\ \Rightarrow l o g (1 + y) (2 + s i n x) = l o g c \\ \Rightarrow (1 + y) (2 + s i n x) = c \\ P u t x = 0 a n d y = 1, w e g e t \\ \Rightarrow (1 + 1) (2 + s i n 0) = c \Rightarrow c = 4 \\ ∴ e q u a t i o n i s (1 + y) (2 + s i n x) = 4 \\ N o w p u t x = \frac{π}{2} \\ ∴ (1 + y) (2 + s i n \frac{π}{2}) = 4 \Rightarrow (1 + y) (2 + 1) = 4 \\ \Rightarrow 1 + y = \frac{4}{3} \Rightarrow y = \frac{4}{3} - 1 = \frac{1}{3} \\ S o, y (\frac{π}{2}) = \frac{1}{3} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s y (\frac{π}{2}) = \frac{1}{3} . \end{array}$

If $y (t)$ is a solution of $(1 + t) \frac{d y}{d t} - t y = 1$ and $y (0) = - 1$ , then show that $y (1) = - \frac{1}{2}$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s (1 + t) \frac{d y}{d t} - t y = 1 \\ \Rightarrow \frac{d y}{d t} - (\frac{t}{1 + t}) y = \frac{1}{1 + t} \\ ∴ P = - \frac{t}{1 + t} a n d Q = \frac{1}{1 + t} \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d t} = e^{\int - \frac{t}{1 + t} . d t} = e^{- \int \frac{1 + t - 1}{1 + t} . d t} \\ = e^{- \int (1 - \frac{1}{1 + t}) . d t} = e^{- [t - l o g (1 + t)]} \\ = e^{- t + l o g (1 + t)} = e^{- t} . e^{l o g (1 + t)} = e^{- t} (1 + t) \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q . I . F . d t + c \\ \Rightarrow y . e^{- t} (1 + t) = \int \frac{1}{(1 + t)} . e^{- t} (1 + t) d t + c \\ \Rightarrow y . e^{- t} (1 + t) = \int e^{- t} d t + c \\ \Rightarrow y . e^{- t} (1 + t) = - e^{- t} + c \\ P u t t = 0 a n d y = - 1 [? y (0) = - 1] \\ \Rightarrow - 1 . e^{0} . 1 = - e^{0} + c \\ \Rightarrow - 1 = - 1 + c \Rightarrow c = 0 \\ S o t h e e q u a t i o n b e c o m e s \\ ∴ y . e^{- t} (1 + 1) = - e^{- t} \\ \Rightarrow 2 y = - 1 \Rightarrow y = - \frac{1}{2} \\ H e n c e, y (1) = - \frac{1}{2} i s v e r i f i e d . \end{array}$

Form the differential equation having $y = {(s i n^{- 1} x)}^{2} + A c o s^{- 1} x + B$ , where $A$ and $B$ are arbitrary constants, as its general solution.

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

Form the differential equation of all circles which pass through the origin and whose centers lie on the y-axis.

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

Find the equation of a curve passing through the origin and satisfying the differential equation $(1 + x^{2}) \frac{d y}{d x} + 2 x y = 4 x^{2} .$

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s (1 + x^{2}) \frac{d y}{d x} + 2 x y = 4 x^{2} \\ \Rightarrow \frac{d y}{d x} + \frac{2 x}{1 + x^{2}} . y = \frac{4 x^{2}}{1 + x^{2}} \\ ∴ P = \frac{2 x}{1 + x^{2}} a n d Q = \frac{4 x^{2}}{1 + x^{2}} \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int \frac{2 x}{1 + x^{2}} . d x} = e^{l o g (1 + x^{2})} = 1 + x^{2} \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y . (1 + x^{2}) = \int \frac{4 x^{2}}{1 + x^{2}} \times (1 + x^{2}) d x + c \\ \Rightarrow y . (1 + x^{2}) = \int 4 x^{2} d x + c \\ \Rightarrow y . (1 + x^{2}) = \frac{4}{3} x^{3} + c \dots (i) \\ Since t h e c u r v e i s passing t h r o u g h i . e ., (0, 0) \\ P u t y = 0 a n d x = 0 i n e q n . (i) \\ \Rightarrow 0 (1 + 0) = \frac{4}{3} {(0)}^{3} + c \Rightarrow c = 0 \\ S o t h e e q u a t i o n b e c o m e s \\ ∴ y (1 + x^{2}) = \frac{4}{3} x^{3} \Rightarrow y = \frac{4 x^{3}}{3 (1 + x^{2})} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s y = \frac{4 x^{3}}{3 (1 + x^{2})} . \end{array}$

Solve: $x^{2} \frac{d y}{d x} = x^{2} + x y + y^{2} .$

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s x^{2} \frac{d y}{d x} = x^{2} + x y + y^{2} \\ \Rightarrow \frac{d y}{d x} = \frac{x^{2} + x y + y^{2}}{x^{2}} \\ P u t y = v x [? I t i s a homogeneous d i f f e r e n t i a l e q u a t i o n] \\ ∴ \frac{d y}{d x} = v + x . \frac{d v}{d x} \\ ∴ v + x . \frac{d v}{d x} = \frac{x^{2} + v x^{2} + v^{2} x^{2}}{x^{2}} \\ \Rightarrow v + x . \frac{d v}{d x} = \frac{x^{2} (1 + v + v^{2})}{x^{2}} \\ \Rightarrow v + x . \frac{d v}{d x} = 1 + v + v^{2} \\ \Rightarrow x . \frac{d v}{d x} = 1 + v + v^{2} - v \\ \Rightarrow x . \frac{d v}{d x} = 1 + v^{2} \Rightarrow \frac{d v}{1 + v^{2}} = \frac{d x}{x} \\ I n t e g r a t i n g b o t h s i d e s w e g e t \\ \int \frac{d v}{1 + v^{2}} = \int \frac{d x}{x} \\ \Rightarrow t a n^{- 1} v = l o g x + c \Rightarrow t a n^{- 1} (\frac{y}{x}) = l o g x + c \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s t a n^{- 1} (\frac{y}{x}) = l o g | x | + c . \end{array}$

Find the general solution of the differential equation $(1 + y^{2}) + (x - e^{t a n^{- 1} y}) \frac{d y}{d x} = 0 .$

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s (1 + y^{2}) + (x - e^{t a n^{- 1} y}) \frac{d y}{d x} = 0 \\ \Rightarrow (x - e^{t a n^{- 1} y}) \frac{d y}{d x} = - (1 + y^{2}) \Rightarrow \frac{d y}{d x} = \frac{- (1 + y^{2})}{x - e^{t a n^{- 1} y}} \\ \Rightarrow \frac{d x}{d y} = \frac{x - e^{t a n^{- 1} y}}{- (1 + y^{2})} \Rightarrow \frac{d x}{d y} = - \frac{x}{(1 + y^{2})} + \frac{e^{t a n^{- 1} y}}{1 + y^{2}} \\ \Rightarrow \frac{d x}{d y} + \frac{x}{(1 + y^{2})} = \frac{e^{t a n^{- 1} y}}{1 + y^{2}} \\ ∴ P = \frac{1}{1 + y^{2}} a n d Q = \frac{e^{t a n^{- 1} y}}{1 + y^{2}} \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d y} = e^{\int \frac{1}{1 + y^{2}} . d y} = e^{t a n^{- 1} y} \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ x \times I . F . = \int Q \times I . F . d y + c \\ \Rightarrow y . e^{t a n^{- 1} y} = \int \frac{e^{t a n^{- 1} y}}{1 + y^{2}} . e^{t a n^{- 1} y} d y + c \\ P u t e^{t a n^{- 1} y} = t \\ ∴ e^{t a n^{- 1} y} . \frac{1}{1 + y^{2}} d y = d t \\ ∴ x . e^{t a n^{- 1} y} = \int t . d t + c \\ \Rightarrow x . e^{t a n^{- 1} y} = \frac{1}{2} t^{2} + c \\ \Rightarrow x . e^{t a n^{- 1} y} = \frac{1}{2} {(e^{t a n^{- 1} y})}^{2} + c \Rightarrow x = \frac{1}{2} (e^{t a n^{- 1} y}) + \frac{c}{e^{t a n^{- 1} y}} \\ \Rightarrow 2 x = e^{t a n^{- 1} y} + \frac{2 c}{e^{t a n^{- 1} y}} \\ \Rightarrow 2 x . e^{t a n^{- 1} y} = {(e^{t a n^{- 1} y})}^{2} + 2 c \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s 2 x . e^{t a n^{- 1} y} = {(e^{t a n^{- 1} y})}^{2} + 2 c . \end{array}$

Find the general solution of $y^{2} d x + (x^{2} - x y + y^{2}) d y = 0$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s y^{2} d x + (x^{2} - x y + y^{2}) d y = 0 \\ \Rightarrow \frac{d x}{d y} = - \frac{x^{2} - x y + y^{2}}{y^{2}} \\ P u t x = v y [? I t i s a homogeneous d i f f e r e n t i a l e q u a t i o n] \\ ∴ \frac{d x}{d y} = v + y . \frac{d v}{d y} \\ ∴ v + y . \frac{d v}{d y} = - (\frac{y^{2} - v y^{2} + v^{2} y^{2}}{y^{2}}) \\ \Rightarrow v + y . \frac{d v}{d y} = - \frac{y^{2} (1 - v + v^{2})}{y^{2}} \\ \Rightarrow v + y . \frac{d v}{d y} = (- 1 + v - v^{2}) \\ \Rightarrow y . \frac{d v}{d y} = - 1 + v - v^{2} - v \\ \Rightarrow y . \frac{d v}{d y} = - 1 - v^{2} \Rightarrow \frac{d v}{v^{2} + 1} = - \frac{d y}{y} \\ I n t e g r a t i n g b o t h s i d e s w e g e t \\ \int \frac{d v}{v^{2} + 1} = - \int \frac{d y}{y} \\ \Rightarrow t a n^{- 1} v = - l o g y + c \Rightarrow t a n^{- 1} (\frac{x}{y}) + l o g y = c \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s t a n^{- 1} (\frac{x}{y}) + l o g y = c . \end{array}$

Solve: $(x + y) (d x - d y) = d x + d y$ .Hint: Substitute $x + y = z$ after separating $d x$ and $d y$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \\ (x + y) (d x - d y) = d x + d y \\ \Rightarrow (x + y) d x - (x + y) d y = d x + d y \\ \Rightarrow - (x + y) d y - d y = d x - (x + y) d x \\ \Rightarrow - (x + y + 1) d y = - (x + y - 1) d x \\ \Rightarrow \frac{d y}{d x} = \frac{x + y - 1}{x + y + 1} \\ P u t x + y = z \\ ∴ 1 + \frac{d y}{d x} = \frac{d z}{d x} \\ \Rightarrow \frac{d y}{d x} = \frac{d z}{d x} - 1 \\ S o, \frac{d z}{d x} - 1 = \frac{z - 1}{z + 1} \\ \Rightarrow \frac{d z}{d x} = \frac{z - 1}{z + 1} \Rightarrow \frac{d z}{d x} = \frac{z - 1 + z + 1}{z + 1} \\ \Rightarrow \frac{d z}{d x} = \frac{2 z}{z + 1} \Rightarrow \frac{z + 1}{z} d z = 2 . d x \\ I n t e g r a t i n g b o t h s i d e s w e g e t \\ \int \frac{z + 1}{z} d z = 2 \int d x \\ \Rightarrow \int (1 + \frac{1}{z}) d z = 2 \int d x \\ \Rightarrow z + l o g | z | = 2 x + l o g | c | \\ \Rightarrow x + y + l o g | x + y | = 2 x + l o g | c | \\ \Rightarrow y + l o g | x + y | = x + l o g | c | \\ \Rightarrow l o g | x + y | = x - y + l o g | c | \\ \Rightarrow l o g | x + y | - l o g | c | = (x - y) \\ \Rightarrow l o g | \frac{x + y}{c} | = (x - y) \\ \Rightarrow \frac{x + y}{c} = e^{x - y} \\ ∴ x + y = c . e^{x - y} \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s x + y = c . \end{array}$

Solve: $2 (y + 3) - x y \frac{d y}{d x} = 0,$ given that $y (1) = - 2$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \\ 2 (y + 3) - x y . \frac{d y}{d x} = 0 \\ \Rightarrow x y . \frac{d y}{d x} = 2 y + 6 \\ \Rightarrow (\frac{y}{2 y + 6}) d y = \frac{d x}{x} \\ \Rightarrow \frac{1}{2} (\frac{y}{y + 3}) d y = \frac{d x}{x} \\ I n t e g r a t i n g b o t h s i d e s w e g e t \\ \frac{1}{2} \int \frac{y}{y + 3} . d y = \int \frac{d x}{x} \\ \Rightarrow \frac{1}{2} \int (1 - \frac{3}{y + 3}) d y = \int \frac{d x}{x} \\ \Rightarrow \frac{1}{2} \int 1 . d y - \frac{3}{2} \int \frac{1}{y + 3} d y = \int \frac{d x}{x} \\ \Rightarrow \frac{1}{2} y - \frac{3}{2} l o g | y + 3 | = l o g x + c \\ P u t x = 1, y = - 2 \\ \Rightarrow \frac{1}{2} (- 2) - \frac{3}{2} l o g | - 2 + 3 | = l o g (1) + c \\ \Rightarrow - 1 - \frac{3}{2} l o g (1) = l o g (1) + c \\ \Rightarrow - 1 - 0 = 0 + c [? l o g (1) = 0] \\ ∴ c = - 1 \\ ∴ e q u a t i o n i s \\ \frac{1}{2} y - \frac{3}{2} l o g | y + 3 | = l o g x - 1 \\ \Rightarrow y - 3 l o g | y + 3 | = 2 l o g x - 2 \\ \Rightarrow y - l o g | {(y + 3)}^{3} | = l o g x^{2} - 2 \\ \Rightarrow l o g | {(y + 3)}^{3} | + l o g x^{2} = y + 2 \\ \Rightarrow l o g | x^{2} {(y + 3)}^{3} | = y + 2 \\ \Rightarrow x^{2} {(y + 3)}^{3} = e^{y + 2} \\ H e n c e, t h e r e q u i r e d s o l \end{array}$

Solve the differential equation $d y = c o s x (2 - y c o s e c x),$ given that $y = 2$ when $x = \frac{π}{2}$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s d y = c o s x (2 - y c o s e c x) d x \\ \Rightarrow \frac{d y}{d x} = c o s x (2 - y c o s e c x) \\ \Rightarrow \frac{d y}{d x} = 2 c o s x - y c o s x . c o s e c x \\ \Rightarrow \frac{d y}{d x} = 2 c o s x - y c o t x \\ \Rightarrow \frac{d y}{d x} + y c o t x = 2 c o s x \\ ∴ P = c o t x a n d Q = 2 c o s x \\ I n t e g r a t i n g f a c t o r I . F = e^{\int P d x} = e^{\int c o t x . d x} = e^{l o g s i n x} = s i n x \\ ∴ S o l u t i o n o f t h e e q u a t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y . s i n x = \int 2 c o s x . s i n x d x + c \\ \Rightarrow y . s i n x = \int s i n 2 x d x + c \Rightarrow y . s i n x = - \frac{1}{2} c o s 2 x + c \\ P u t x = \frac{π}{2} a n d y = 2, w e g e t \\ 2 . s i n \frac{π}{2} = - \frac{1}{2} c o s 2 . \frac{π}{2} + c \\ \Rightarrow 2 (1) = - \frac{1}{2} c o s π + c \Rightarrow 2 = - \frac{1}{2} (- 1) + c \\ \Rightarrow 2 = \frac{1}{2} + c \Rightarrow c = 2 - \frac{1}{2} = \frac{3}{2} \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s y s i n x = - \frac{1}{2} c o s 2 x + \frac{3}{2} . \end{array}$

Form the differential equation by eliminating $A$ and $B$ in $A x^{2} + B y^{2} = 1$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s A x^{2} + B y^{2} = 1 \\ D i f f e r e n t i a t i n g w . r . t . x, w e g e t \\ \Rightarrow 2 A . x + 2 B y \frac{d y}{d x} = 0 \\ \Rightarrow A . x + B y \frac{d y}{d x} = 0 \\ \Rightarrow B y . \frac{d y}{d x} = - A x \Rightarrow \frac{y}{x} . \frac{d y}{d x} = - \frac{A}{B} \\ D i f f e r e n t i a t i n g b o t h s i d e s a g a i n w . r . t . x, w e h a v e \\ \frac{y}{x} . \frac{d^{2} y}{d x^{2}} + \frac{d y}{d x} (\frac{x . \frac{d y}{d x} - y . 1}{x^{2}}) = 0 \\ \Rightarrow \frac{y x^{2}}{x} . \frac{d^{2} y}{d x^{2}} + x . {(\frac{d y}{d x})}^{2} - y . \frac{d y}{d x} = 0 \\ \Rightarrow x y . \frac{d^{2} y}{d x^{2}} + x . {(\frac{d y}{d x})}^{2} - y . \frac{d y}{d x} = 0 \\ \Rightarrow x y . y^{''} + x . {(y^{'})}^{2} - y . y^{'} = 0 \\ H e n c e, t h e r e q u i r e d e q u a t i o n i s x y . y^{''} + x . {(y^{'})}^{2} - y . y^{'} = 0 \end{array}$

Solve the differential equation $(1 + y^{2}) t a n^{- 1} x d x + 2 y (1 + x^{2}) d y = 0 .$

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \\ (1 + y^{2}) t a n^{- 1} x d x + 2 y (1 + x^{2}) d y = 0 \\ \Rightarrow 2 y (1 + x^{2}) d y = - (1 + y^{2}) . t a n^{- 1} x . d x \\ \Rightarrow \frac{2 y}{1 + y^{2}} d y = - \frac{t a n^{- 1} x}{1 + x^{2}} . d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{2 y}{1 + y^{2}} d y = - \int \frac{t a n^{- 1} x}{1 + x^{2}} . d x \\ \Rightarrow l o g | 1 + y^{2} | = - \frac{1}{2} {(t a n^{- 1} x)}^{2} + c \\ \Rightarrow \frac{1}{2} {(t a n^{- 1} x)}^{2} + l o g | 1 + y^{2} | = c \\ H e n c e, t h e r e q u i r e d s o l u t i o n i s \frac{1}{2} {(t a n^{- 1} x)}^{2} + l o g | 1 + y^{2} | = c . \end{array}$

Find the differential equation of the system of concentric circles with center $(1, 2)$ .

This is a Short Answer Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} F a m i l y o f c o n c e n t r i c c i r c l e s w i t h c e n t r e (1, 2) a n d r a d i u s' r' i s \\ {(x - 1)}^{2} + {(y - 2)}^{2} = r^{2} \\ D i f f e r e n t i a t i n g b o t h s i d e s w . r . t . x, w e g e t \\ 2 (x - 1) + 2 (y - 2) \frac{d y}{d x} = 0 \\ \Rightarrow (x - 1) + (y - 2) \frac{d y}{d x} = 0 \\ W h i c h i s t h e r e q u i r e d e q u a t i o n . \end{array}$

Choose the correct answer from the given four options in each of the Exercises from 1 to 42 (M.C.Q)

Q1.The degree of the differential equation ${(\frac{d^{2} y}{d x^{2}})}^{2} + {(\frac{d y}{d x})}^{2} = x s i n x (\frac{d y}{d x})$ is:

(A) 1

(B) 2

(C) 3

(D) Not defined

This is a Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e degree o f g i v e n d i f f e r e n t i a l e q u a t i o n i s n o t d e f i n e d b e c a u s e t h e v a l u e o f \\ s i n (\frac{d y}{d x}) o n expansionwillbeincreasing p o w e r o f (\frac{d y}{d x}) . \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The degree of the differential equation ${[1 + {(\frac{d y}{d x})}^{2}]}^{\frac{3}{2}} = \frac{d^{2} y}{d x^{2}}$ is

(A) 4

(B) $\frac{3}{2}$

(C) Not defined

(D) 2

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ {[1 + {(\frac{d y}{d x})}^{2}]}^{3 / 2} = (\frac{d^{2} y}{d x^{2}}) \\ S q u a r i n g b o t h s i d e s, w e h a v e \\ {[1 + {(\frac{d y}{d x})}^{2}]}^{3} = {(\frac{d^{2} y}{d x^{2}})}^{2} \\ S o, t h e degree o f t h e g i v e n d i f f e r e n t i a l e q u a t i o n i s 2 . \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The order and degree of the differential equation $\frac{d^{2} y}{d x^{2}} + {(\frac{d y}{d x})}^{\frac{1}{4}} + x^{\frac{1}{5}} = 0$ respectively, are

(A) 2 and not defined

(B) 2 and 2

(C) 2 and 3

(D) 3 and 3

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d^{2} y}{d x^{2}} + {(\frac{d y}{d x})}^{\frac{1}{4}} + x^{\frac{1}{5}} = 0 \\ \Rightarrow \frac{d^{2} y}{d x^{2}} + {(\frac{d y}{d x})}^{\frac{1}{4}} = - x^{\frac{1}{5}} \\ Since, t h e o f \frac{d y}{d x} i s i n f r a c t i o n . \\ S o, t h e degree o f t h e g i v e n d i f f e r e n t i a l e q u a t i o n i s n o t d e f i n e d a s t h e o r d e r i s 2 . \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

If $y = e^{- x} (A c o s x + B s i n x)$ , then $y$ is a solution of

(A) $\frac{d^{2} y}{d x^{2}} + 2 \frac{d y}{d x} = 0$

(B) $\frac{d^{2} y}{d x^{2}} - 2 \frac{d y}{d x} + 2 y = 0$

(C) $\frac{d^{2} y}{d x^{2}} + 2 \frac{d y}{d x} + 2 y = 0$

(D) $\frac{d^{2} y}{d x^{2}} + 2 y = 0$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s y = e^{- x} (A c o s x + B s i n x) \\ d i f f e r e n t i a t i n g b o t h s i d e s, w . r . t . x, w e g e t \\ \frac{d y}{d x} = e^{- x} (- A s i n x + B c o s x) - e^{- x} (A c o s x + B s i n x) \\ \frac{d y}{d x} = e^{- x} (- A s i n x + B c o s x) - y \\ A g a i n d i f f e r e n t i a t i n g b o t h s i d e s, w . r . t . x, w e g e t \\ \frac{d^{2} y}{d x^{2}} = e^{- x} (- A c o s x - B s i n x) - e^{- x} (- A s i n x + B c o s x) - \frac{d y}{d x} \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - e^{- x} (A c o s x + B s i n x) - [\frac{d y}{d x} + y] - \frac{d y}{d x} \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - y - \frac{d y}{d x} - y - \frac{d y}{d x} \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - 2 \frac{d y}{d x} - 2 y \Rightarrow \frac{d^{2} y}{d x^{2}} + 2 \frac{d y}{d x} + 2 y = 0 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The differential equation for $y = A c o s α x + B s i n α x$ , where A and B are arbitrary constants, is

(A) $\frac{d^{2} y}{d x^{2}} - α^{2} y = 0$

(B) $\frac{d^{2} y}{d x^{2}} + α^{2} y = 0$

(C) $\frac{d^{2} y}{d x^{2}} + α y = 0$

(D) $\frac{d^{2} y}{d x^{2}} - α y = 0$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s y = A c o s α x + B s i n α x \\ d i f f e r e n t i a t i n g b o t h s i d e s, w . r . t . x, w e g e t \\ \frac{d y}{d x} = - A s i n α x . α + B c o s α x . α \\ \frac{d y}{d x} = - A α s i n α x + B α c o s α x \\ A g a i n d i f f e r e n t i a t i n g b o t h s i d e s, w . r . t . x, w e g e t \\ \frac{d^{2} y}{d x^{2}} = - A α^{2} c o s α x - B α^{2} s i n α x \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - α^{2} (A c o s α x + B s i n α x) \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - α^{2} y \\ \Rightarrow \frac{d^{2} y}{d x^{2}} + α^{2} y = 0 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Solution of the differential equation $x d y - y d x = 0$ represents:

(A) A rectangular hyperbola

(B) A parabola whose vertex is at the origin

(C) A straight line passing through the origin

(D) A circle whose center is at the origin

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \\ x d y - y d x = 0 \\ \Rightarrow \frac{d y}{d x} = \frac{y}{x} \Rightarrow \frac{d y}{y} = \frac{d x}{x} \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{d y}{y} = \int \frac{d x}{x} \\ \Rightarrow l o g y = l o g x + l o g c \\ \Rightarrow l o g y = l o g x c \\ \Rightarrow y = x c w h i c h i s a s t r a i g h t l i n e passing t h r o u g h t h e o r i g i n . \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Integrating factor of the differential equation $c o s x \frac{d y}{d x} + y s i n x = 1$ is:

(A) $cosx$

(B) $tanx$

(C) $secx$

(D) $sinx$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n d i f f e r e n t i a l e q u a t i o n i s \\ c o s x . \frac{d y}{d x} + y s i n x = 1 \\ \Rightarrow \frac{d y}{d x} + \frac{s i n x}{c o s x} y = \frac{1}{c o s x} \Rightarrow \frac{d y}{d x} + t a n x y = s e c x \\ H e r e, P = t a n x a n d Q = s e c x \\ I n t e g r a t i n g f a c t o r = e^{\int P d x} = e^{\int t a n x d x} = e^{l o g s e c x} = s e c x \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

$S o l u t i o n o f t h e d i f f e r e n t i a l e q u a t i o n t a n y s e c^{2} x d x + t a n x s e c^{2} y d y = 0$ is:

(A) $tanx + tany = k$

(B) $tanx -tan y = k$

(C) $\frac{tanx}{tany} = k$

(D) $tanx \cdot tany = k$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ t a n y s e c^{2} x d x + t a n x s e c^{2} y d y = 0 \\ \Rightarrow t a n x s e c^{2} y d y = - t a n y s e c^{2} x d x \\ \Rightarrow \frac{s e c^{2} y}{t a n y} . d y = \frac{- s e c^{2} x}{t a n x} . d x \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \Rightarrow \int \frac{s e c^{2} y}{t a n y} . d y = \int \frac{- s e c^{2} x}{t a n x} . d x \\ \Rightarrow l o g | t a n y | = - l o g | t a n x | + l o g c \\ \Rightarrow l o g | t a n y | + l o g | t a n x | = l o g c \\ \Rightarrow l o g | t a n x . t a n y | = l o g c \\ \Rightarrow t a n x . t a n y = k [? l o g c = k] \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

Family $y = A x + A^{3}$ of curves is represented by the differential equation of degree:

(A) 1

(B) 2

(C) 3

(D) 4

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} G i v e n e q u a t i o n i s y = A x + A^{3} \\ D i f f e r e n t i a t i n g b o t h s i d e s, w e g e t \\ \frac{d y}{d x} = A w h i c h h a s degree 1 . \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

Integrating factor of $x \frac{d y}{d x} - y = x^{4} - 3 x$ is:

(A) $x$

(B) $logx$

(C) $\frac{1}{x}$

(D) $- x$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ x \frac{d y}{d x} - y = x^{4} - 3 x \\ \frac{d y}{d x} - \frac{y}{x} = x^{3} - 3 \\ H e r e, P = - \frac{1}{x} a n d Q = x^{3} - 3 \\ S o, integrating f a c t o r = e^{\int P d x} = e^{\int - \frac{1}{x} d x} = e^{- l o g x} = e^{l o g \frac{1}{x}} = \frac{1}{x} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

Solution of $\frac{d y}{d x} - y = 1, y (0) = 1$ is given by

(A) $x y = - e^{x}$

(B) $x y = - e^{- x}$

(C) $x y = - 1$

(D) $y = 2 e^{x} - 1$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} - y = 1 \\ H e r e, P = - 1 a n d Q = 1 \\ S o, integrating f a c t o r = e^{\int P d x} = e^{\int - 1 d x} = e^{- x} \\ S o, t h e s o l u t i o n i s \\ y \times I . F = \int Q \times I . F . d x + c \\ \Rightarrow y \times e^{- x} = \int 1 . e^{- x} . d x + c \\ \Rightarrow y . e^{- x} = - e^{- x} + c \\ P u t x = 0, y = 1 \\ \Rightarrow 1 . e^{0} = - e^{0} + c \\ \Rightarrow 1 = - 1 + c ∴ c = 2 \\ S o, t h e e q u a t i o n i s y . e^{- x} = - e^{- x} + 2 \\ \Rightarrow y = - 1 + 2 e^{x} = 2 e^{x} - 1 \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The number of solutions of $\frac{d y}{d x} + \frac{y + 1}{x - 1} = 1$ when $y (1) = 2$ is:

(A) None

(B) One

(C) Two

(D) Infinite

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} = \frac{y + 1}{x - 1} \\ \Rightarrow \frac{d y}{y + 1} = \frac{d x}{x - 1} \\ integrating b o t h s i d e s, w e g e t \\ \int \frac{d y}{y + 1} = \int \frac{d x}{x - 1} \\ \Rightarrow l o g (y + 1) = l o g (x - 1) + l o g c \\ \Rightarrow l o g (y + 1) - l o g (x - 1) = l o g c \\ \Rightarrow l o g | \frac{y + 1}{x - 1} | = l o g c \\ \Rightarrow \frac{y + 1}{x - 1} = c \\ P u t x = 1 a n d y = 2 \\ \Rightarrow \frac{2 + 1}{1 - 1} = c ∴ c = \infty \\ \Rightarrow \frac{y + 1}{x - 1} = \frac{1}{0} \Rightarrow x - 1 = 0 \\ \Rightarrow x = 1 \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Which of the following is a second-order differential equation?

(A) ${(y^{'})}^{2} + x = y^{2}$

(B) $y^{'} y^{'} + y = sinx$

(C) $y^{'} + {(y^{'})}^{2} + y = 0$

(D) $y^{'} = y^{2}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} second o r d e r d i f f e r e n t i a l e q u a t i o n i s y^{'} y^{''} + y = s i n x \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

Integrating factor of the differential equation $(1 - x^{2}) \frac{d y}{d x} - x y = 1$

(A) $- x$

(B) $x + 1$

(C) $1 - x^{2}$

(D) $log(1 - x^{2})$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol: $\begin{array}{l} \end{array}$

$t a n^{- 1} x + t a n^{- 1} y = c$ is the general solution of the differential equation:

(A) $\frac{d y}{d x} + \frac{1 + y^{2}}{1 + x^{2}}$

(B) $\frac{d y}{d x} + \frac{1 + x^{2}}{1 + y^{2}}$

(C) $(1 + x^{2}) d y + (1 + y^{2}) d x = 0$
(D) $(1 + x^{2}) d x + (1 + y^{2}) d y = 0$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n e q u a t i o n i s t a n^{- 1} x + t a n^{- 1} y = c \\ D i f f e r e n t i a t i n g w . r . t . x, w e h a v e \\ \Rightarrow \frac{1}{1 + x^{2}} + \frac{1}{1 + y^{2}} . \frac{d y}{d x} = 0 \\ \Rightarrow (\frac{1}{1 + y^{2}}) \frac{d y}{d x} = - (\frac{1}{1 + x^{2}}) \\ \Rightarrow \frac{d y}{d x} = - (\frac{1 + y^{2}}{1 + x^{2}}) \\ \Rightarrow (1 + x^{2}) d y = - (1 + y^{2}) d x \\ \Rightarrow (1 + x^{2}) d y + (1 + y^{2}) d x = 0 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The differential equation $y \frac{d y}{d x} + x = c$ represents:

(A) Family of hyperbolas

(B) Family of parabolas

(C) Family of ellipses

(D) Family of circles

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n D i f f e r e n t i a l e q u a t i o n i s y \frac{d y}{d x} + x = c \\ \Rightarrow y \frac{d y}{d x} = c - x y d y = (c - x) d x \\ ∴ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \Rightarrow \int y d y = \int (c - x) d x \\ \Rightarrow \frac{y^{2}}{2} = c x - \frac{x^{2}}{2} + k \\ \Rightarrow \frac{x^{2}}{2} + \frac{y^{2}}{2} - c x = k \\ \Rightarrow x^{2} + y^{2} - 2 c x = 2 k w h i c h i s a f a m i l y o f c i r c l e s . \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The general solution of $e^{x} c o s y d x - e^{x} s i n y d y = 0$ is:

(A) $e^{x} cosy = k$

(B) $e^{x} siny = k$

(C) $e^{x} = k cos y$

(D) $e^{x} = ksin y$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n D i f f e r e n t i a l e q u a t i o n i s e^{x} c o s y d x - e^{x} s i n y d y = 0 \\ \Rightarrow e^{x} (c o s y d x - s i n y d y) = 0 \\ \Rightarrow c o s y d x - s i n y d y = 0 [? e^{x} \neq 0] \\ \Rightarrow s i n y d y = c o s y d x \\ \Rightarrow \frac{s i n y}{c o s y} d y = d x \\ ∴ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \Rightarrow \int \frac{s i n y}{c o s y} d y = \int d x \\ \Rightarrow - l o g | c o s y | = x + l o g k \Rightarrow l o g \frac{1}{c o s y} - l o g k = x \\ \Rightarrow l o g (\frac{1}{k c o s y}) = x \Rightarrow \frac{1}{k c o s y} = e^{x} \\ \Rightarrow \frac{1}{k} = e^{x} c o s y \Rightarrow e^{x} c o s y = c [? c = \frac{1}{k}] \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The degree of the differential equation $\frac{d^{2} y}{d x^{2}} {(\frac{d y}{d x})}^{3} + 6 y^{5} = 0$ is:

(A) 1

(B) 2

(C) 3

(D) 5

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e degree o f t h e g i v e n D i f f e r e n t i a l e q u a t i o n i s 1 a s t h e p o w e r o f t h e h i g h e s t o r d e r i s 1 . \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The solution of $\frac{d y}{d x} + y = x e^{- x}, y (0) = 0$ is:

(A) $y = e^{x} (x - 1)$

(B) $y = x e^{- x}$

(C) $y = x e^{- x} + 1$

(D) $y = (x + 1) e^{- x}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} + y = e^{- x} \\ since i t i s l i n e a r d i f f e r e n t i a l e q u a t i o n \\ ∴ P = 1 a n d Q = e^{- x} \\ ∴ I . F . = e^{\int 1 . d x} = e^{x} \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \Rightarrow y \times e^{x} = \int e^{- x} . e^{x} d x + c \\ \Rightarrow y \times e^{x} = \int 1 . d x + c \Rightarrow y . e^{x} = x + c \\ P u t x = 0, y = 0, w e h a v e 0 = 0 + c ∴ c = 0 \\ S o, t h e s o l u t i o n i s y . e^{x} = x \Rightarrow y = x . e^{- x} \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The integrating factor of the differential equation $\frac{d y}{d x} + y t a n x - s e c x = 0$ is:

(A) Cos $x$

(B) $Secx$

(C) $e^{cosx}$

(D) $e^{secx}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

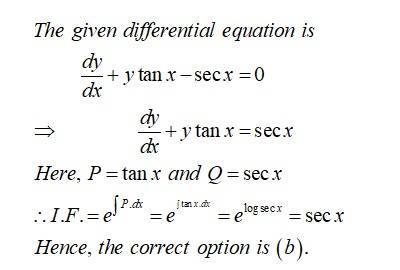
The solution of the differential equation $\frac{d y}{d x} + \frac{1 + y^{2}}{1 + x^{2}}$ is:

(A) $y =tan^{- 1} x$

(B) $y - x = k (1 + x y)$

(C) $x =tan^{- 1} y$

(D) $tan(x y) = k$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} = \frac{1 + y^{2}}{1 + x^{2}} \\ \Rightarrow \frac{d y}{1 + y^{2}} = \frac{d x}{1 + x^{2}} \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{d y}{1 + y^{2}} = \int \frac{d x}{1 + x^{2}} \\ \Rightarrow t a n^{- 1} y = t a n^{- 1} x + c \Rightarrow t a n^{- 1} y - t a n^{- 1} x = c \\ \Rightarrow t a n^{- 1} (\frac{y - x}{1 + x y}) = c \Rightarrow \frac{y - x}{1 + x y} = t a n c \\ \Rightarrow \frac{y - x}{1 + x y} = k [? k = t a n c] \\ \Rightarrow y - x = k (1 + x y) \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The integrating factor of the differential equation $\frac{d y}{d x} + y = \frac{1 + y}{x}$ is:

(A) $x / e^{x^{x}}$

(B) $e^{x} / x$

(C) $x e^{x}$

(D) $e^{x}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$y = A e^{m x} + B e^{- m x}$ satisfies which of the following differential equations?

(A) $\frac{d y}{d x} + m y = 0$

(B) $\frac{d y}{d x} - m y = 0$

(C) $\frac{d^{2} y}{d x^{2}} - m^{2} y = 0$

(D) $\frac{d^{2} y}{d x^{2}} + m^{2} y = 0$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n e q u a t i o n i s y = a e^{m x} + b e^{- m x} \\ O n, d i f f e r e n t i a t i o n, w e g e t \\ \frac{d y}{d x} = a . m e^{m x} - b . m e^{- m x} \\ A g a i n d i f f e r e n t i a t i n g w . r . t x, w e h a v e \\ \frac{d^{2} y}{d x^{2}} = a m^{2} e^{m x} + b m^{2} e^{- m x} \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = m^{2} (a e^{m x} + b e^{- m x}) \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = m^{2} y \Rightarrow \frac{d^{2} y}{d x^{2}} - m^{2} y = 0 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The solution of the differential equation $c o s x s i n y d x + s i n x c o s y d y = 0$ is:

(A) $\frac{Sinx}{Siny} = c$

(B) $sinxsin y = c$

(C) $sinx + siny = c$

(D) $cosx cos y = c$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ c o s x s i n y d x + s i n x c o s y d y = 0 \\ \Rightarrow s i n x c o s y d y = - c o s x s i n y d x \\ \Rightarrow \frac{c o s y}{s i n y} d y = - \frac{c o s x}{s i n x} d x \Rightarrow c o t y d y = - c o t x d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int c o t y d y = - \int c o t x d x \\ \Rightarrow l o g | s i n y | = - l o g | s i n x | + l o g c \\ \Rightarrow l o g | s i n y | + l o g | s i n x | = l o g c \\ \Rightarrow l o g | s i n y . s i n x | = l o g c \\ \Rightarrow s i n x . s i n y = c \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The solution of $\frac{d y}{d x} + y = e^{x}$ is:

(A) $y = e^{x} / x + k / x$

(B) $y = x e^{x} + c x$

(C) $y = x e^{x} + k$

(D) $x = \frac{e^{y}}{y} + \frac{k}{y}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s x \frac{d y}{d x} + y = e^{x} \\ \Rightarrow \frac{d y}{d x} + \frac{y}{x} = \frac{e^{x}}{x} \\ H e r e, P = \frac{1}{x} a n d Q = \frac{e^{x}}{x} \\ ∴ I n t e g r a t i n g f a c t o r I . F . = e^{\int P . d x} = e^{\int \frac{1}{x} . d x} = e^{l o g | x |} = x \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + k \Rightarrow y \times x = \int \frac{e^{x}}{x} . x d x + k \\ \Rightarrow y \times x = \int e^{x} d x + k \Rightarrow y \times x = e^{x} + k \\ ∴ y = \frac{e^{x}}{x} + \frac{k}{x} \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The differential equation of the family of curves $x^{2} + y^{2} - 2 a y = 0,$ where a is an arbitrary constant, is:

(A) $(x^{2} - y^{2}) \frac{d y}{d x} = 2 x y$

(B) $2 (x^{2} + y^{2}) \frac{d y}{d x} = x y$

(C) $2 (x^{2} - y^{2}) \frac{d y}{d x} = x y$

(D) $(x^{2} + y^{2}) \frac{d y}{d x} = 2 x y$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n e q u a t i o n i s x^{2} + y^{2} - 2 a y = 0 \dots (i) \\ D i f f e r e n t i a t i n g w . r . t x w e h a v e \\ 2 x + 2 y . \frac{d y}{d x} - 2 a \frac{d y}{d x} = 0 \\ \Rightarrow x + y \frac{d y}{d x} - a \frac{d y}{d x} = 0 \Rightarrow x + (y - a) \frac{d y}{d x} = 0 \\ \Rightarrow (y - a) \frac{d y}{d x} = - x \Rightarrow y - a = \frac{- x}{d y / d x} \\ \Rightarrow a = \frac{- x}{d y / d x} + y \Rightarrow a = \frac{y . \frac{d y}{d x} + x}{\frac{d y}{d x}} \\ P u t t i n g t h e v a l u e o f a i n e q n . (i) w e g e t \\ \Rightarrow x^{2} + y^{2} - 2 y [\frac{y . \frac{d y}{d x} + x}{\frac{d y}{d x}}] = 0 \\ \Rightarrow (x^{2} + y^{2}) \frac{d y}{d x} - 2 y (y . \frac{d y}{d x} + x) = 0 \\ \Rightarrow (x^{2} + y^{2}) \frac{d y}{d x} - 2 y^{2} \frac{d y}{d x} - 2 x y = 0 \\ \Rightarrow (x^{2} + y^{2} - 2 y^{2}) \frac{d y}{d x} = 2 x y \Rightarrow (x^{2} - y^{2}) \frac{d y}{d x} = 2 x y \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The family $y = A x + A^{3}$ of curves corresponds to a differential equation of order:

(A) 3

(B) 2

(C) 1

(D) Not defined

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n e q u a t i o n i s y = A x + A^{3} \\ D i f f e r e n t i a t i n g b o t h s i d e s, w e g e t \frac{d y}{d x} = A \\ A g a i n d i f f e r e n t i a t i n g b o t h s i d e s, w e g e t \frac{d^{2} y}{d x^{2}} = 0 \\ S o, t h e o r d e r o f t h e d i f f e r e n t i a l e q u a t i o n i s 2 . \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The general solution of $\frac{d y}{d x} = 2 x e^{x - y}$ is:

(A) $e^{- x} y = c$

(B) $e^{- y} + e^{x^{2}} = c$

(C) $e^{y} = e^{x^{2}} + c$

(D) $e^{x^{2 + y}} = c$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} = 2 x . e^{x^{2} - y} \Rightarrow \frac{d y}{d x} = 2 x . e^{x^{2}} . e^{- y} \\ \Rightarrow \frac{d y}{e^{- y}} = 2 x . e^{x^{2}} d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int \frac{d y}{e^{- y}} = \int 2 x . e^{x^{2}} d x \\ \Rightarrow \int e^{y} d y = \int 2 x . e^{x^{2}} d x [\begin{array}{l} P u t i n R . H . S . x^{2} = t \\ ∴ 2 x d x = d t \end{array}] \\ \Rightarrow \int e^{y} d y = \int e^{t} d t \\ \Rightarrow e^{y} = e^{t} + c \Rightarrow e^{y} = e^{x^{2}} + c \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The curve for which the slope of the tangent at any point is equal to the ratio of the abscissa to the ordinate of the point is:

(A) An ellipse

(B) A parabola

(C) A circle

(D) A rectangular hyperbola

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} Since, t h e s l o p e o f t h e t o t h e c u r v e = x : y \\ ∴ \frac{d y}{d x} = \frac{x}{y} \Rightarrow y d y = x d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \int y d y = \int x d x \\ \Rightarrow \frac{y^{2}}{2} = \frac{x^{2}}{2} + c \Rightarrow y^{2} = x^{2} + 2 c \\ \Rightarrow y^{2} - x^{2} = 2 c = k w h i c h i s rectangular h y p e r b o l a . \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The general solution of the differential equation $\frac{d y}{d x} = e^{x^{2} / 2} + x y$ is:

(A) $y = c e^{- \frac{x^{2}}{2}}$

(B) $y = c e^{\frac{x^{2}}{2}}$

(C) $y = (x + c) e^{\frac{x^{2}}{2}}$

(D) $y = c - x e^{\frac{x^{2}}{2}}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} = e^{\frac{x^{2}}{2}} + x y \Rightarrow \frac{d y}{d x} - x y = e^{\frac{x^{2}}{2}} \\ Since i t i s l i n e a r d i f f e r e n t i a l e q u a t i o n w h e r e P = - x a n d Q = e^{\frac{x^{2}}{2}} \\ ∴ I . F . = e^{\int P . d x} = e^{\int - x . d x} = e^{\frac{- x^{2}}{2}} \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \Rightarrow y \times e^{\frac{- x^{2}}{2}} = \int e^{\frac{x^{2}}{2}} . e^{\frac{- x^{2}}{2}} d x + c \\ \Rightarrow y \times e^{\frac{- x^{2}}{2}} = \int e^{0} . d x + c \Rightarrow y . e^{\frac{- x^{2}}{2}} = \int 1 . d x + c \\ \Rightarrow y . e^{\frac{- x^{2}}{2}} = x + c \\ ∴ y = (x + c) e^{\frac{x^{2}}{2}} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The solution of the equation $(2 y - 1) d x - (2 x + 3) d y = 0$ is:

(A) $\frac{2 x - 1}{2 y + 3} = k$

(B) $\frac{2 y + 1}{2 x - 3} = k$

(C) $\frac{2 x + 3}{2 y - 1} = k$

(D) $\frac{2 x - 1}{2 y - 1} = k$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ (2 y - 1) d x - (2 x + 3) d y = 0 \\ \Rightarrow (2 x + 3) d y = (2 y - 1) d x \\ \Rightarrow \frac{d y}{2 y - 1} = \frac{d x}{2 x + 3} \\ I n t e g r a t i n g b o t h s i d e s, w e g e t \\ \int \frac{d y}{2 y - 1} = \int \frac{d x}{2 x + 3} \\ \Rightarrow \frac{1}{2} l o g | 2 y - 1 | = \frac{1}{2} l o g | 2 x + 3 | + l o g c \\ \Rightarrow l o g | 2 y - 1 | = l o g | 2 x + 3 | + 2 l o g c \\ \Rightarrow l o g | 2 y - 1 | - l o g | 2 x + 3 | = l o g c^{2} \\ \Rightarrow l o g | \frac{2 y - 1}{2 x + 3} | = l o g c^{2} \\ \Rightarrow \frac{2 y - 1}{2 x + 3} = c^{2} \Rightarrow \frac{2 x + 3}{2 y - 1} = \frac{1}{c^{2}} \\ \Rightarrow \frac{2 x + 3}{2 y - 1} = k, w h e r e k = \frac{1}{c^{2}} \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The differential equation for which $y = a c o s x + b s i n x$ is a solution, is:

(A) $\frac{d^{2} y}{d x^{2}} + y = 0$

(B) $\frac{d^{2} y}{d x^{2}} - y = 0$

(C) $\frac{d^{2} y}{d x^{2}} + (a + b) y = 0$

(D) $\frac{d^{2} y}{d x^{2}} + (a - b) y = 0$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n e q u a t i o n i s y = a c o s x + b s i n x \\ ∴ \frac{d y}{d x} = - a s i n x + b c o s x \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - a c o s x - b s i n x \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - (a c o s x + b s i n x) \\ \Rightarrow \frac{d^{2} y}{d x^{2}} = - y \Rightarrow \frac{d^{2} y}{d x^{2}} + y = 0 \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The solution of $\frac{d y}{d x} + y = e^{- x}, y (0) = 0$ is:

(A) $y = e^{- x} (x - 1)$

(B) $y = x e^{x}$

(C) $y = x e^{- x} + 1$

(D) $y = x e^{- x}$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \frac{d y}{d x} + y = e^{- x} Since$
$\begin{array}{l} it i s l i n e a r d i f f e r e n t i a l e q u a t i o n w h e r e P = 1 a n d Q = e^{- x} \\ ∴ I . F . = e^{\int P . d x} = e^{\int 1 . d x} = e^{x} \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \Rightarrow y \times e^{x} = \int e^{- x} . e^{x} d x + c \\ \Rightarrow y \times e^{x} = \int e^{0} . d x + c \Rightarrow y . e^{x} = \int 1 . d x + c \\ \Rightarrow y . e^{x} = x + c \\ P u t y = 0 a n d x = 0 \\ ∴ 0 = (0 + c) ∴ c = 0 \\ ∴ e q u a t i o n i s y . e^{x} = x \\ S o, y = x . e^{- x} \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The order and degree of the differential equation ${(\frac{d^{3} y}{d x^{3}})}^{2} - 3 {(\frac{d^{2} y}{d x^{2}})}^{3} + {(\frac{d y}{d x})}^{4} = y^{4}$ are:

(A) 1, 4

(B) 3, 4

(C) 2, 4

(D) 3, 2

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ {[\frac{d^{3} y}{d x^{3}}]}^{2} - 3 \frac{d^{2} y}{d x^{2}} + 2 {(\frac{d y}{d x})}^{4} = y^{4} \\ H e r e, t h e h i g h e s t d e r i v a t i v e i s \frac{d^{3} y}{d x^{3}} . \\ ∴ o r d e r o f t h e d i f f e r e n t i a l e q u a t i o n i s 3 \\ a n d t h e p o w e r o f t h e h i g h e s t d e r i v a t i v e i s 2 \\ ∴ i t s degreeis 2 \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

The order and degree of the differential equation ${[1 + {(\frac{d y}{d x})}^{2}]}^{} + \frac{d^{2} y}{d x^{2}} = 0$ are:

(A) 2, 3/2

(B) 2, 3

(C) 2, 1

(D) 3, 4

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ [1 + {(\frac{d y}{d x})}^{2}] = \frac{d^{2} y}{d x^{2}} \\ H e r e, t h e h i g h e s t d e r i v a t i v e i s 2, \\ ∴ o r d e r = 2 \\ a n d t h e p o w e r o f t h e h i g h e s t d e r i v a t i v e i s 1 \\ ∴ degree = 1 \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The differential equation of the family of curves $y^{2} = 4 a (x + a)$ is:

(A) $y^{2} 4 \frac{d y}{d x} = (x + \frac{d y}{d x})$

(B) $2 y \frac{d y}{d x} = 4 a$

(C) $y \frac{d^{2} y}{d x^{2}} + {\frac{d y}{d x}}^{2} = 0$

(D) $2 x \frac{d y}{d x} + y {(\frac{d y}{d x})}^{2} - y$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n e q u a t i o n o f f a m i l y o f c u r v e s i s \\ y^{2} = 4 a (x + a) \\ \Rightarrow y^{2} = 4 a x + 4 a^{2} \dots (i) \\ D i f f e r e n t i a t i n g b o t h s i d e s, w . r . t . x, w e g e t \\ 2 y . \frac{d y}{d x} = 4 a \\ \Rightarrow y . \frac{d y}{d x} = 2 a \Rightarrow \frac{y}{2} . \frac{d y}{d x} = a \\ N o w, p u t t i n g t h e v a l u e o f a i n e q n . (i) w e g e t \\ y^{2} = 4 x (\frac{y}{2} . \frac{d y}{d x}) + 4 {(\frac{y}{2} . \frac{d y}{d x})}^{2} \\ \Rightarrow y^{2} = 2 x y \frac{d y}{d x} + y^{2} {(\frac{d y}{d x})}^{2} \\ \Rightarrow y = 2 x \frac{d y}{d x} + y {(\frac{d y}{d x})}^{2} \\ \Rightarrow 2 x . \frac{d y}{d x} + y . {(\frac{d y}{d x})}^{2} - y = 0 \\ H e n c e, t h e c o r r e c t o p t i o n i s (d) . \end{array}$

Which of the following is the general solution of $\frac{d^{2} y}{d x^{2}} - 2 \frac{d y}{d x} + y = 0$ ?

(A) $y = (A x + B) e^{x}$

(B) $y = (A x + B) e^{- x}$

(C) $y = A e^{x} + B e^{- x}$

(D) $y = A cosx + B sinx$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \frac{d^{2} y}{d x^{2}} - 2 \frac{d y}{d x} + y = 0 \\ Since t h e a b o v e e q u a t i o n i s o f o r d e r a n d f i r s t \\ ∴ D^{2} y - 2 D y + y = 0, w h e r e D = \frac{d}{d x} \\ \Rightarrow (D^{2} - 2 D + 1) = 0 \\ ∴ a u x i l i a r y e q u a t i o n i s m^{2} - 2 m + 1 = 0 \\ \Rightarrow {(m - 1)}^{2} = 0 \Rightarrow m = 1, 1 \\ I f t h e r o o t s o f A u x i l i a r y e q u a t i o n a r e r e a l a n d e q u a l s a y (m) t h e n, \\ C F = (c_{1} x + c_{2}) . e^{m x} \\ ∴ C F = (A x + B) . e^{x} \\ S o, y = (A x + B) . e^{x} \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The general solution of $\frac{d y}{d x} + y t a n x = s e c x$ is:

(A) $y secx =tan x + c$

(B) $y tanx = secx + c$

(C) tan $x = y tanx + c$

(D) $x sec x =tan y + c$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} + y t a n x = s e c x \\ Since i t i s l i n e a r d i f f e r e n t i a l e q u a t i o n w h e r e P = t a n x a n d Q = s e c x \\ ∴ I . F . = e^{\int P . d x} = e^{\int t a n x . d x} = e^{l o g s e c x} = s e c x \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y \times s e c x = \int s e c x . s e c x d x + c \\ \Rightarrow y \times s e c x = \int s e c^{2} x . d x + c \\ \Rightarrow y s e c x = t a n x + c \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The solution of the differential equation $s i n x \frac{d y}{d x} + y = x$ is:

(A) $x (y + cosx) = sinx + c$

(B) $x (y - cosx) = sinx + c$

(C) $x ycos x = sinx + c$

(D) $x (y + cosx) = cosx + c$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \frac{d y}{d x} + \frac{y}{x} = s i n x \\ Since i t i s l i n e a r d i f f e r e n t i a l e q u a t i o n w h e r e P = \frac{1}{x} a n d Q = s i n x \\ ∴ I . F . = e^{\int P . d x} = e^{\int \frac{1}{x} . d x} = e^{l o g x} = x \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y \times x = \int s i n x . x d x + c \Rightarrow y \times x = \int x s i n x . d x + c \\ \Rightarrow y x = x . \int s i n x d x - \int (D (x) \int s i n x d x) d x + c \\ \Rightarrow y x = x (- c o s x) - \int - c o s x d x + c \\ \Rightarrow y x = - x c o s x + \int c o s x d x + c \\ \Rightarrow y x = - x c o s x + s i n x + c \\ \Rightarrow y x + x c o s x = s i n x + c \\ \Rightarrow x (y + c o s x) = s i n x + c \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

The general solution of the differential equation $(e^{x} + 1) y d y = (y + 1) e^{x} d x$ is:

(A) $y + 1 = k (e^{x} + 1)$

(B) $y + 1 = e^{x} + 1 + k$

(C) $y = l o g {k (y + 1) (e^{x} + 1)}$

(D) y $= (e^{x} + 1 / y + 1) +k$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ (e^{x} + 1) y d y = (y + 1) e^{x} d x \\ \Rightarrow \frac{y}{y + 1} d y = \frac{e^{x}}{e^{x} + 1} d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \Rightarrow \int \frac{y}{y + 1} d y = \int \frac{e^{x}}{e^{x} + 1} d x \\ \Rightarrow \int \frac{y + 1 - 1}{y + 1} d y = \int \frac{e^{x}}{e^{x} + 1} d x \\ \Rightarrow \int 1 . d y + \int \frac{1}{y + 1} d y = \int \frac{e^{x}}{e^{x} + 1} d x \\ \Rightarrow y - l o g | y + 1 | = l o g | e^{x} + 1 | + l o g k \\ \Rightarrow y = l o g | y + 1 | + l o g | e^{x} + 1 | + l o g k \\ \Rightarrow y = l o g | k (y + 1) (e^{x} + 1) | \\ H e n c e, t h e c o r r e c t o p t i o n i s (c) . \end{array}$

The solution of the differential equation $\frac{d y}{d x} = e^{x - y} + x^{2} e^{- y}$ is:

(A) $y = e^{y - y} - x^{2} e^{- y} + c$

(B) $e^{y} - e^{x} = x^{3} / 3 + c$

(C) $e^{x} + e^{y} = x^{3} / 3 + c$

(D) $e^{x} - e^{y} = x^{3} / 3 + c$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} = e^{x - y} + x^{2} e^{- y} \\ \Rightarrow \frac{d y}{d x} = e^{x} . e^{- y} + x^{2} e^{- y} \Rightarrow \frac{d y}{d x} = e^{- y} (e^{x} + x^{2}) \\ \Rightarrow \frac{d y}{e^{- y}} = (e^{x} + x^{2}) d x \Rightarrow e^{y} . d y = (e^{x} + x^{2}) d x \\ I n t e g r a t i n g b o t h s i d e s, w e h a v e \\ \Rightarrow \int e^{y} . d y = \int (e^{x} + x^{2}) d x \\ \Rightarrow e^{y} = e^{x} + \frac{x^{3}}{3} + c \\ \Rightarrow e^{y} - e^{x} = \frac{x^{3}}{3} + c \\ H e n c e, t h e c o r r e c t o p t i o n i s (b) . \end{array}$

The solution of $\frac{d y}{d x} + \frac{2 x y}{1 + x^{2}} = \frac{1}{1 + x^{2}}$ is:

(A) $y (1 + x^{2}) = c +tan^{- 1} x$

(B) $\frac{y}{1 + x^{2}} = c +tan^{- 1} x$

(C) $ylog (1 + x^{2}) = c +tan^{- 1} x$

(D) $y (1 + x^{2}) = c +sin^{- 1} x$

This is an Objective Type Questions as classified in NCERT Exemplar

Sol:

$\begin{array}{l} T h e g i v e n d i f f e r e n t i a l e q u a t i o n i s \\ \frac{d y}{d x} + \frac{2 x y}{1 + x^{2}} = \frac{1}{{(1 + x^{2})}^{2}} \\ since i t i s l i n e a r d i f f e r e n t i a l e q u a t i o n w h e r e P = \frac{2 x y}{1 + x^{2}} a n d Q = \frac{1}{{(1 + x^{2})}^{2}} \\ ∴ I . F . = e^{\int P . d x} = e^{\int \frac{2 x y}{1 + x^{2}} . d x} = e^{l o g (1 + x^{2})} = (1 + x^{2}) \\ S o, t h e s o l u t i o n i s \\ y \times I . F . = \int Q \times I . F . d x + c \\ \Rightarrow y (1 + x^{2}) = \int \frac{1}{{(1 + x^{2})}^{2}} \times (1 + x^{2}) d x + c \\ \Rightarrow y (1 + x^{2}) = \int \frac{1}{(1 + x^{2})} . d x + c \\ \Rightarrow y (1 + x^{2}) = t a n^{- 1} x + c \\ H e n c e, t h e c o r r e c t o p t i o n i s (a) . \end{array}$

JEE Mains Solution 2022

Commonly asked questions

Let R be a relation from the set ${1, 2, 3, . . . . ., 60}$ to itself such that R = ${(a, b) : b = p q}$ where p, q $\geq$ 3 are prime numbers. Then, the number of elements in R is:

R = { (a, b): b = pq, where p, q $\geq 3$ are prime}

$\Rightarrow 60 \times 11 = 660$

p, q $\in$ {3, 5, 7, 11, 13, 17, 19, 23, 29, 3, 37, 41, 43, 47, 53, 59} total 16

p, q $\in$ {3, 5, 7, 11, 13, 17, 19}

{3, 5, 7, 11, 13, 17, 19}

7 + 3 + 1 = 11

If z = 2 + 3 i, then z5 + ${(\bar{z})}^{5}$ is equal to:

$z^{5} + {(\bar{z})}^{5}$

$= {(2 + 3 i)}^{5} + {(2 - 3 i)}^{5}$

$= 2 (32 - 720 + 810) = 244$

Let A and B be two 3 × 3 non-zero real matrices such that AB is a zero matrix. Then

$A_{3 \times 3}, B_{3 \times 3} & A B = 0$

$\neq 0 \neq 0 \Rightarrow | A | = 0 & | B | = 0$ only .

$\frac{1}{(20 - a) (40 - a)} + \frac{1}{(40 - a) (60 - a)} + . . . + \frac{1}{(180 - a) (200 - a)} = \frac{1}{256},$ then the maximum value of a is:

$\frac{1}{(20 - a) (40 - a)} + \frac{1}{(40 - a) (60 - a)} + \frac{1}{(60 - a) (80 - a)} + . . . . . + \frac{1}{(180 - a) (200 - a)} = \frac{1}{256}$

LHS = $\frac{1}{20} (\frac{1}{20 - a} - \frac{1}{40 - a}) + \frac{1}{20} (\frac{1}{40 - a} - \frac{1}{60 - a}) + . . . + \frac{1}{20} (\frac{1}{180 - a} - \frac{1}{200 - a})$

$= \frac{1}{20} (\frac{1}{20 - a} - \frac{1}{200 - a}) = \frac{1}{20} . \frac{180}{(20 - a) (200 - a)}$

$\Rightarrow a^{2} - 220 a + 4000 - 2304 = 0 \Rightarrow a^{2} 220 a + 1696 = 0$

$a = \frac{220 \pm 204}{8} = 21 2^{2}$

If $\underset{x \to 0}{l i m} \frac{α e^{x} + β e^{- x} + γ s i n x}{x s i n^{2} x} = \frac{2}{3},$ where $α, β, γ \in R,$ then which of the following is NOT correct?

$\underset{x \to 0}{l i m} \frac{α e^{x} + β e^{- x} + γ s i n x}{x s i n^{2} x}$

$= \underset{x \to 0}{l i m} \frac{α e^{x} + β e^{- x} + γ s i n x}{x^{3}}$

$\Rightarrow α + β = 0, α - β + γ = 0, \frac{α + β}{2} = 0, \frac{α}{6} - \frac{β}{6} - \frac{γ}{6} = \frac{2}{3}$

$\Rightarrow β = - α γ = - 2 α α - β - γ = 4 \Rightarrow α + α + 2 α = 4 \Rightarrow γ = 1$

$α = 1, β = - 1, γ = - 2$

The integral $\int_{0}^{\frac{π}{2}} \frac{1}{3 + 2 s i n x + c o s x} d x$ is equal to:

$\int_{0}^{\frac{π}{2}} \frac{d x}{3 + 2 s i n x + c o s x} P u t t a n \frac{x}{2} = t \Rightarrow \frac{1}{2} s e c^{2} \frac{x}{2} d x = d t$

$= \int_{0}^{1} \frac{2 d t}{2 t^{2} + 4 t + 4} = \int_{0}^{1} \frac{d t}{{(t + 1)}^{2} + 1} = {[t a n^{- 1} (t + 1)]}_{0}^{1} = t a n^{- 1} 2 - t a n^{- 1} 1$

Let the solution curve y = y(x) of the differential equation $(1 + e^{2 x}) (\frac{d y}{d x} + y) = 1$ pass through the point $(0, \frac{π}{2}) .$ Then, $\underset{x \to \infty}{l i m} e^{x} y (x)$ is equal to:

IF =e^x

$y e^{x} = \int \frac{e^{x}}{1 + e^{2 x}} d x$

$\int \frac{d t}{1 + t^{2}}$

= tan^-1 (t) + c

$\underset{x \to \infty}{l i m} e^{x} y = \underset{x \to \infty}{l i m} t a n^{- 1} e^{x} + \frac{π}{4} = \frac{3 π}{4}$

Let a line L pass through the point of intersection of the lines bx + 10y – 8 = 0 and $2 x - 3 y = 0, b \in R - {\frac{4}{3}} .$ If the line L also passes through the point (1, 1) and touches the circle 17(x2 + y2) = 16, then the eccentricity of the ellipse $\frac{x^{2}}{5} + \frac{y^{2}}{b^{2}} = 1$ is:

y – 1 = m(x – 1)

mx – y + 1 – m = 0

$\frac{| 1 - m |}{\sqrt[]{m^{2} + 1}} = \frac{4}{\sqrt[]{17}}$

$17 {(1 - m)}^{2} = 16 (m^{2} + 1)$

m² – 3m + 1 = 0

$\begin{array}{l} b x + 10 y - 8 = 0 \\ y = \frac{2}{3} x \end{array}} \Rightarrow (b + \frac{20}{3}) x = 8$

$x = \frac{24}{3 b + 20}, y = \frac{16}{3 b + 20}$

b = $\frac{2 (3 - 2 \sqrt[]{2}) (4 + 3 \sqrt[]{2})}{- 2}$

$= \frac{12 - 8 \sqrt[]{2} + 9 \sqrt[]{2}}{- 1} = - \sqrt[]{2}$

b² = 2

$\frac{x^{2}}{5} + \frac{y^{2}}{2} = 1$

2 = 5 (1 – e²)

$e^{2} = \frac{3}{5}$

$e$ $=$

IF the foot of the perpendicular from the point A(1, 4, 3) on the plane P : 2x + my + nz = 4, is $(- 2, \frac{7}{2}, \frac{3}{2}),$ then the distance of the point A form the plane P, measured parallel to a line with direction ratios 3, 1, 4, is equal to:

A (1, 4, 3)

2x + my + nz = 4

$M \Rightarrow - 4 + \frac{7 m}{2} + \frac{3 n}{2} = 4$

7m + 3n = 16

$\vec{A M} = (- 1, \frac{- 1}{2}, \frac{- 3}{2})$

$\frac{2}{- 1} = \frac{m}{\frac{- 1}{2}} = \frac{n}{\frac{- 3}{2}}$

m = 1, n = 3

Plane : 2x + y + 3z = 4

$c o s θ = \frac{| 6 - 1 - 12 |}{\sqrt[]{26} \sqrt[]{14}} = \frac{7}{2 \sqrt[]{91}}$

AM = $\frac{| - 2 + 4 + 9 - 4 |}{\sqrt[]{14}} = \frac{7}{\sqrt[]{14}}$

$c$ $o$ $s$ $θ$ $=$ $\frac{A M}{A B}$ $\Rightarrow$ $A$ $B$ $=$ $\frac{7 / 14}{7 / 291}$ $=$ $\frac{291}{14}$ $=$ $2$ $\frac{13 \times 7}{2 \times 7}$ $=$

Let $\vec{a} = 3 \hat{i} + \hat{j} a n d \vec{b} = \hat{i} + 2 \hat{j} + \hat{k} .$ Let $\vec{c}$ be vector satisfying $\vec{a} \times (\vec{b} \times \vec{c}) = \vec{b} + λ \vec{c} .$ If $\vec{b} a n d \vec{c}$ are non-parallel, then the value of $λ$ is:

$(\overset{?}{a} . \overset{?}{c}) \overset{?}{b} ? (\overset{?}{a} . \overset{?}{b}) \overset{?}{c}$

$= \overset{?}{b} + ? \overset{?}{c} (g i v e n)$

$\overset{?}{a} . \overset{?}{c} = 1, ? = ? \overset{?}{a} . \overset{?}{b}$

$? = ? (3, 1, 0) . (1, 2, 1)$

= (3 + 2)= 5

The angle of elevation of the top of a tower from a point A due north of it and from a point B at a distance of 9 units due west of A is $c o s^{- 1} (\frac{3}{\sqrt[]{13}}) .$ If the distance of the point B from the tower is 15 units, then cot is equal to:

$100 c o t^{2} α = 1 5^{2} - 9^{2} = 144$

$\frac{O T}{15} = \frac{2}{3}$

$c o t α = \frac{6}{5} O T = 10$

$Δ A O T, O A = O T c o t α = 10 c o t α$

The statement $(p \land q) \Rightarrow (p \land r)$ is equivalent to:

$(p \land q) \to (p \land r)$

$\equiv \sim (p \land q) \lor (p \land r)$

$(A) (\sim q) \lor (p \land r) (B) (\sim p) \lor (p \land r)$

$(C) \sim (p \land r) \lor (p \land q) (D) \sim (p \land q) \lor r$

Option (D) is correct

Let the circumcentre of a triangle with vertices A(a, 3), B(b, 5) and C(a, b), ab > 0 be P(1, 1). If the line AP intersects the line BC at the point Q(k1, k2), then k1 + k2 is equal to:

${(a - 1)}^{2} + 4 = {(b - 1)}^{2} + 16$

$= {(a - 1)}^{2} + {(b - 1)}^{2}$

${(b - 1)}^{2} = 4 & {(a - 1)}^{2} = 16$

$\Rightarrow b = 1 \pm 2 a = 1 \pm 4$

= 3, 1= 5, 3

x + 2y = 3 …… (i)

3x – y = 8…… (ii)

x + 2y = 3

3x – y = 83 × 2

$\oplus \to 7 x = - 13 \Rightarrow x = \frac{- 13}{7}$

$y = \frac{- 39}{7} + 8 = \frac{17}{7}$

$k_{1} + k_{2} = x + y = \frac{4}{7}$

Let $\hat{a} a n d \hat{b}$ be two unit vectors such that the angle between them is $\frac{π}{4} .$ If is the angle between the vectors $(\hat{a} + \hat{b}) a n d (\hat{a} + 2 \hat{b} + 2 (\hat{a} \times \hat{b})),$ then the value of 164cos2 is equal to:

$(\hat{a} + \hat{b}) . (\hat{a} + 2 \hat{b} + 2 (\hat{a} \times \hat{b})), \hat{a} . \hat{b} = \frac{1}{\sqrt[]{2}}$

= 1 + $\frac{1}{\sqrt[]{2}} + \sqrt[]{2}$ + 2 + 0 + 0

$= 3 + \frac{3}{\sqrt[]{2}}$

$| \hat{a} + 2 \hat{b} + 2 {(\hat{a} \times \hat{b})}^{2} | = 1 + 4 + 4 (\frac{1}{2}) + 2 \sqrt[]{2} + 0 = 7 + 2 \sqrt[]{2}$

$\Rightarrow (2 + \sqrt[]{2}) (7 + 2 \sqrt[]{2}) c o s^{2} θ = 9 + \frac{9}{2} + 9 \sqrt[]{2} = \frac{27 + 18 \sqrt[]{2}}{2}$

$\Rightarrow c o s^{2} θ = \frac{27 + 18 \sqrt[]{2}}{2} \times \frac{1}{18 + 11 \sqrt[]{2}} = \frac{(27 + 18 \sqrt[]{2}) (18 - 11 \sqrt[]{2})}{2 (324 - 242)}$

$= \frac{486 + 324 \sqrt[]{2} - 297 \sqrt[]{2} - 396}{2 \times 82}$

164 cos² (θ)= 90 + $2$ $7$

If f(X) = $\int_{1}^{α} \frac{l o g_{10} t}{1 + t} d t, α > 0, t h e n f (e^{3}) + f (e^{- 3}) i s e q u a l t o :$

$f (α) = \int_{1}^{α} \frac{l o g_{10} t}{1 + t} d t$

$f (\frac{1}{α}) = \int_{1}^{\frac{1}{α}} \frac{l o g_{10} t}{1 + t} d t = \int_{1}^{α} \frac{- l o g_{10} z}{1 + \frac{1}{z}} - \frac{1}{z^{2}} d z$

$= \int_{1}^{α} \frac{l o g_{10} z}{z (z + 1)} d z$

$= \int_{1}^{α} \frac{l o g_{10} t}{t} d t = \frac{1}{l n 10} \int_{1}^{α} \frac{l n t}{t} d t = \frac{1}{l n 10} {[\frac{{(l n t)}^{2}}{2}]}_{1}^{α} = \frac{{(l n α)}^{2}}{2 l n 10}$

$f (e^{3}) + f (e^{- 3}) = \frac{{(l n e^{3})}^{2}}{2 l n 10} = \frac{9}{2 l n 10}$

The area of the region ${(x, y) : | x - 1 | \leq y \leq \sqrt[]{5 - x^{2}}}$ is equal to:

$| x - 1 | \leq y \leq \sqrt[]{5 - x^{2}}$

$y = | x - 1 |, y^{2} + x^{2} = 5, y \geq 0 y = \sqrt[]{5 - x^{2}}$

${(x - 1)}^{2} + x^{2} = 5 \Rightarrow 2 x^{2} - 2 x - 4 = 0 \Rightarrow x^{2} - x - 2 = 0$

$(x - 2) (x + 1) = 0 \to x = - 1, 2$

$A = \int_{- 1}^{2} (\sqrt[]{5 - x^{2}} - | x - 1 |) d x$

$A r e a = \int_{- 1}^{2} (\sqrt[]{5 - x^{2}} d x - | x - 1 | d x)$

$= \int_{- 1}^{2} \sqrt[]{5 - x^{2}} d x + \int_{- 1}^{1} (x - 1) d x - \int_{1}^{2} (x - 1) d x$

$= \frac{5}{2} s i n^{- 1} (1) - \frac{1}{2} = \frac{5 π}{4} - \frac{1}{2}$

Let the focal chord of the parabola P : y² = 4x along the line L : y = mx + c, m > 0 meet the parabola at the points M and N. Let the line L be a tangent to the hyperbola H : x² – y² = 4. If O is the vertex of P and F is the focus of H on the positive x-axis, then the area of the quadrilateral OMFN is:

L : y = mx + c, m > 0

y = m (x – 1)

$\frac{x^{2}}{4} - \frac{y^{2}}{4} = 1$

$y = m x \pm \sqrt[]{4 m^{2} - 4}$

$\pm \sqrt[]{4 m^{2} - 4} = - m, m > 0$

$\Rightarrow \sqrt[]{4 m^{2} - 4} = m$

$M (\frac{5 + \sqrt[]{21}}{2}, \sqrt[]{3} + \sqrt[]{7}), N (\frac{5 - \sqrt[]{21}}{2}, \sqrt[]{3} - \sqrt[]{7})$

$=$ $2$ $(27)$ $=$ $2$

The number of points, where the function f : R R,

$f (x) = | x - 1 | c o s | x - 2 | s i n | x - 1 | + (x - 3) | x^{2} - 5 x + 4 |,$ is NOT differentiable, is:

$f (x) = | x - 1 | c o s | x - 2 | s i n | x - 1 | + (x - 3) | x^{2} - 5 x + 4 |$

$f (x) = | x - 1 | c o s (x - 2) s i n | x - 1 | + (x - 3) | x - 1 | | x - 4 |$

x = 1, 4 (doubtful points)

Diff. at x = 1

$\underset{x \to 1}{l i m} \frac{f (x) - f (1)}{x - 1} = \underset{x \to 1}{l i m} \frac{| x - 1 | (s i n | x - 1 | c o s (x - 2) + (x - 3) | x - 4 |)}{x - 1}$

$\begin{array}{l} R H D = \underset{x \to 4^{+}}{l i m} \frac{3 (s i n 3 c o s 2)}{0^{+}} = + \infty \\ L H D = \underset{x \to 4^{-}}{l i m} \frac{3 (s i n 3 c o s 2)}{0^{-}} = - \infty \end{array}} \Rightarrow$ Not diff. at x = 4

Let S = {1, 2, 3,…., 2022}. Then the probability, that a randomly chosen number n from the set S such that HCF (n, 2022) = 1, is:

S = {1,2, 3, …., n, 2022}

HCF (n, 2022) = 1

2022 = 2 × 1011 ->3 × 337

2022 = 2 × 3 × 337 (prime factorization)

Let n (A) = no members divisible by 2 = 1011

Let n (B) = no members divisible by 3 = 674

Let n (C) = no members divisible by 337 = 6

$n (A \cup B \cup C) = n (A) + n (B) + n (C) - n (A \cap B) - n (B \cap C) - n (C \cap A) + n (A \cap B \cap C)$

= 1011 + 674 + 6 – 337 – 2 – 3 + 1

= 1350

$n (A \cap B) = 337$

$n ((A \cup B \cup C)') = 2022 - 1350 = 672$

Prob. $= \frac{672}{2022} = \frac{336}{1011} = \frac{112}{337}$

Let f(x) = $3^{{(x^{2} - 2)}^{3} + 4}, x \in R .$ Then which of the following statements are true?

P : x = 0 is a point of local minima of f

Q : x = $\sqrt[]{2}$ is a point of inflection of f

R : $f'$ is increasing for x > $\sqrt[]{2}$

$f (x) = 3^{{(x^{2} - 2)}^{3} + 4} = 81 . 3^{{(x^{2} - 2)}^{3}}$

$f' (x) = 81 . 3^{{(x^{2} - 2)}^{3}} . l n 3.3 {(x^{2} - 2)}^{2} . 2 x$

From graph : P, Q, R

Let $S = {θ \in (0, 2 π) : 7 c o s^{2} θ - 3 s i n^{2} θ - 2 c o s^{2} 2 θ = 2} .$ Then, the sum of roots of all the equations $x^{2} - 2 (t a n^{2} θ + c o t^{2} θ) x + 6 s i n^{2} θ = 0, θ \in S, i s . . . . . . . . .$

$\frac{7}{2} (1 + c o s 2 θ) - \frac{3}{2} (1 - c o s 2 θ) - 2 c o s^{2} 2 θ = 2$

Put cos 2 $θ$ = t

Equation 2t²– 5t = 0, t (2t – 5) = 0

$t = 0, \frac{5}{2}$

cos 20 = 0, 0 < 2 < 4

$x_{1} + x_{2} = 2 (t a n^{2} θ + c o t^{2} θ) \Rightarrow ?$

$= 2 (1 + 1) + 2 (1 + 1) + 2 (1 + 1) + 2 (1 + 1) = 16$

Let the mean and the variance of 20 observations x1, x2,…….x20 be 15 and 9, respectively. For $\in R$ , if the mean of ${(x_{1} + α)}^{2}, {(x_{2} + α)}^{2}, . . . ., {(x_{20} + α)}^{2}$ is 178, then the square of the maximum value of is equal to………….

$\bar{x} = 15 \Rightarrow \sum_{i = 1}^{20} x_{i} = 300$

$\frac{\sum_{i = 1}^{20} {(x_{i} - 15)}^{2}}{20} = 9 \Rightarrow \sum_{i = 1}^{20} {(x_{i} - 15)}^{2} = 180$

$\sum_{i = 1}^{20} {(x_{i} + α)}^{2} = 178 \times 20 = 3560$

$4680 + 2 α (300) + 20 α^{2} = 3560$

$α^{2} + 30 α + 234 - 178 = 0$

= 2, 28

$α_{m a x} 2 = {(- 2)}^{2} = 4$

Let a line with direction ratios a, 4a, 7 be perpendicular to the lines with direction ratios 3, 1, 2b and b, a, 2. If the point of intersection of the line $\frac{x + 1}{a^{2} + b^{2}} = \frac{y - 2}{a^{2} - b^{2}} = \frac{z}{1}$ and the plane x – y + z = 0 is $(α, β, γ), t h e n α + β + γ$ is equal to………

(a, 4a, 7). (3, 1, 2b)= 0

3a + 4a – 14b = 0 a – 2b = 0 ……. (i)

(a, 4a, 7) . (b, a, 2) = 0

ab – 4a² + 14 = 0……… (ii)

(i) & (ii) =>2b² – 16b²+ 14 = 0

$\Rightarrow b^{2} = 1 \Rightarrow a = 2 b = \pm 2$

Plane : x – y + z = 0

P (4, 5, 1)

4 + 5 + 1 = 10

Le aa₁, a₂, a₃,…… be an A.P. If $\sum_{r = 1}^{\infty} \frac{a_{r}}{2^{r}} = 4,$ then 4a₂ is equal to……

$\sum_{r = 1}^{\infty} \frac{a + (r - 1) d}{2^{r}} = 4, 4 (a + d) = ?$

$\Rightarrow a \sum_{r = 1}^{\infty} {(\frac{1}{2})}^{r} + d \sum_{r = 1}^{\infty} (r - 1) {(\frac{1}{2})}^{r} = 4$

$= {(\frac{1}{2})}^{2} \sum_{k = 0}^{\infty} k {(\frac{1}{2})}^{k - 1}$

$= \frac{1}{4} . \frac{1}{{(1 - \frac{1}{2})}^{2}}$

= 1

a + d = 4

4 (a + d) = 16

Let the ratio of the fifth term from the beginning to the fifth term from the end in the binomial

$T_{5} =^{n} C_{4} {(2^{\frac{1}{4}})}^{n - 4} . {({(\frac{1}{3})}^{\frac{1}{4}})}^{4} =^{n} C_{4} . 2^{\frac{n - 4}{4}} . \frac{1}{3}$

$T_{6} =^{9} C_{5} {(2^{\frac{1}{2}})}^{4} . {({(\frac{1}{3})}^{\frac{1}{4}})}^{5} =^{9} C_{5} . 2 . \frac{1}{3^{5 / 4}} = \frac{2}{3} . \frac{1}{3^{\frac{1}{4}}} . \frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1}$

The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is……….

$A = [\begin{matrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \\ c_{1} & c_{2} & c_{3} \end{matrix}], a_{2}, b_{2}, c_{2} \in {0, 1}$

S = $a_{1} + a_{2} + a_{3} + b_{1} + b_{2} + b_{3} + c_{1} + c_{2} + c_{3}$ is prime

$0 \leq s \leq 9$

Prime value = 2,3, 5, 7

$F o r S = 2, 1 + 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 \to \frac{9!}{2! 7!} = 36$

Total number of matrices

= 36 + 84 + 126 + 36 = 282

Let p and p + 2 be prime numbers and let

$Δ = | \begin{matrix} p! & (p + 1)! & (p + 2)! \\ (p + 1)! & (p + 2)! & (p + 3)! \\ (p + 2)! & (p + 3)! & (p + 4)! \end{matrix} |$

Then the sum, of the maximum values of and , such that p and (p + 2) divide $Δ,$ is…………..

$Δ = p! (p + 1)! (p + 2)! Δ_{1} = 2 p! (p + 1); (p + 2)! = 2 {(p!)}^{3} . {(p + 1)}^{2} . {(p + 2)}^{1} \to α + β = 3 + 1 = 4$

$Δ_{1} = | \begin{matrix} 1 & p + 1 & (p + 2) (p + 1) \\ 1 & p + 2 & (p + 3) (p + 2) \\ 1 & p + 3 & (p + 4) (p + 3) \end{matrix} | = | \begin{matrix} 0 & - 1 & (p + 2) (- 2) \\ 0 & - 1 & (p + 3) (- 2) \\ 1 & p + 3 & (p + 4) (p + 3) \end{matrix} |$

= 2(p + 3) – 2 (p + 2) = 2

If $\frac{1}{2 \times 3 \times 4} + \frac{1}{3 \times 4 \times 5} + \frac{1}{4 \times 5 \times 6} + . . . + \frac{1}{100 \times 101 \times 102} = \frac{k}{101},$ then 34 k is equal to………….

$t_{n} = \frac{1}{(n + 1) (n + 2) (n + 3)}, n = 1, 2, 3, . . . ., 99$

$= \frac{1}{2} (\frac{1}{(n + 1) (n + 2)} - \frac{1}{(n + 2) (n + 3)}) = V_{n} - V_{n + 1}$

$= \frac{1}{12} (\frac{1716}{101 \times 17}) = \frac{143}{101 \times 17} = \frac{k}{101} \Rightarrow k = \frac{143}{17}$

34 k = 286

Let S = {4, 6, 9} and T = {9, 10, 11,…., 1000}.

If A = ${a_{1} + a_{2} + . . . + a_{k} : k \in N, a_{1}, a_{2}, a_{3}, . . . . ., a_{k} \in S},$ then the sum of all the elements in the set T – A is equal to…………….

T = {9, 10, 11, 12, …., 1000}

S = {4, 6, 9}

A = ${a_{1} + a_{2} + . . . . + a_{k} : k \in N, a_{i} \in S}$

Let 4 appear x no. of times

6 appear y no. of times

9 appear z no. of times

10 then set A has n element 4x + 6y + 9z

Concept : Let a and b are co-prime numbers, then members from (a - ) (b – 1) and more can be expressed in the form ax + by where x, y $\in$ {0, 1, 2, …}

So, all the number of the form

2y + 3z are (2 1). (3 – 1), ….

i.e., 6, 7, 8, 9, 10, 11, ….

form : 2 + t, t = 0, 1, 2, 3, ….

So, 6y + 9z = 3 (2y + 3z) = 3 (2 + t) = 6 + 3t, t = 0, 1, 2, 3, …

sum of element of T – A is 11

Let the mirror image of a circle c₁ : x² + y² – 2x – 6y + a = 0 in line y = x + 1 be c₂ : 5x² + 5y² + 10gx + 10fy + 38 = 0. If r is the radius of circle c₂, then a + 6r² is equal to…………..

${(x - 1)}^{2} + {(y - 3)}^{2} = 10 - α$

$\begin{array}{l} x - y = - 1 \\ x + y = a + b \end{array}} \to m (\frac{a + b - 1}{2}, \frac{a + b + 1}{2})$

A’ = 2m – A = (b – 1, a + 1)

$C_{2} : x^{2} + y^{2} + 2 g x + 2 f y + \frac{38}{5} = 0$

r $\sqrt[]{g^{2} + f^{2} - c}$

$= \sqrt[]{4 + 4 - \frac{38}{5}} = \sqrt[]{\frac{2}{5}}$

$C_{1} : \sqrt[]{\frac{2}{5}} = \sqrt[]{1 + 9 - α} = \sqrt[]{10 - α}$

$α + 6 r^{2} = \frac{48}{5} + 6 (\frac{2}{5}) = \frac{60}{5} = 12$

Maths NCERT Exemplar Solutions Class 12th Chapter Nine Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Differential Equations

News & Updates

Latest NewsPopular News

Maths NCERT Exemplar Solutions Class 12th Chapter Nine: Overview, Questions, Preparation

Differential Equations Questions and Answers

Commonly asked questions

JEE Mains Solution 2022

Commonly asked questions

Student Forum

Other Similar chapters for you

News & Updates

CBSE CTET FEB 2026 Notification @ctet.nic.in- LIVE Updates on Application, Eligibility & Last Date

UPSSSC UP PET Result 2025 LIVE (TODAY)- Check Expected Cut-Off & Download Link @upsssc.gov.in

JEE Main 2026 Application Form Live: NTA Registration Last Date To Apply November 27; Latest Updates

IBPS PO 2025 Mains Result LIVE- Download Link Soon @ibps.in & Check Previous Years Cut Off Here

RBSE Exam Date Sheet 2026 Class 10, 12 Anytime Soon; Live Updates on Rajasthan Board Secondary, Senior Secondary Exam

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement