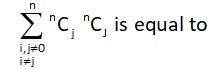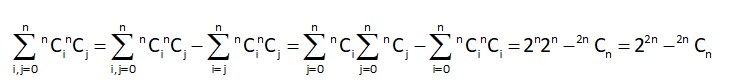- Probability Questions and Answers
- JEE Mains Solutions 2022, 26th july , Maths second shift
- 27th July 2022 first shift
Probability Questions and Answers
| Q1. Three bags contain a number of red and white balls as follows: Bag 1: 3 red balls, Bag 2: 2 red balls and 1 white ball, Bag 3: 3 white balls. The probability that bag will be chosen and a ball is selected from it is , where . What is the probability that: i. A red ball will be selected? ii. A white ball is selected? |
| Sol:
|
| Q2. Refer to Question 41 above. If a white ball is selected, what is the probability that it came from
|
| Sol:
|
| Q3. A shopkeeper sells three types of flower seeds: , , and . They are sold as a mixture where the proportions are 4:4:2, respectively. The germination rates of the three types of seeds are 45%, 60%, and 35%. Calculate the probability: (i) Of a randomly chosen seed to germinate (ii) That it will not germinate given that the seed is of type (iii) That it is of type given that a randomly chosen seed does not germinate. |
| Sol:
|
| Q4. A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letters "TA" are visible. What is the probability that the letter came from TATA NAGAR? |
| Sol:
|
Commonly asked questions
Three bags contain a number of red and white balls as follows:
Bag 1: 3 red balls, Bag 2: 2 red balls and 1 white ball, Bag 3: 3 white balls. The probability that bag will be chosen and a ball is selected from it is , where . What is the probability that:
i. A red ball will be selected?
ii. A white ball is selected?
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Refer to Question 41 above. If a white ball is selected, what is the probability that it came from
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
A shopkeeper sells three types of flower seeds: , , and . They are sold as a mixture where the proportions are 4:4:2, respectively. The germination rates of the three types of seeds are 45%, 60%, and 35%. Calculate the probability:
(i) Of a randomly chosen seed to germinate
(ii) That it will not germinate given that the seed is of type
(iii) That it is of type given that a randomly chosen seed does not germinate.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
A letter is known to have come either from TATA NAGAR or from CALCUTTA. On the envelope, just two consecutive letters "TA" are visible. What is the probability that the letter came from TATA NAGAR?
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
There are two bags, one of which contains 3 black and 4 white balls while the other contains 4 black and 3 white balls. A die is thrown. If it shows up 1 or 3, a ball is taken from the first bag; if it shows up any other number, a ball is chosen from the second bag. Find the probability of choosing a black ball.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
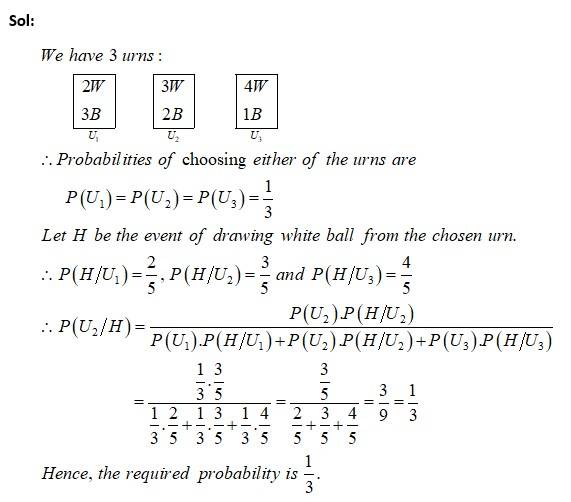
There are three urns containing: 2 white and 3 black balls 3 white and 2 black balls 4 white and 1 black ball respectively. There is an equal probability of each urn being chosen. A ball is drawn at random from the chosen urn, and it is found to be white. Find the probability that the ball drawn was from the second urn.
This is a Long Answer Type Questions as classified in NCERT Exemplar
By examining the chest X-ray, the probability that TB is detected when a person is actually suffering is 0.99. The probability of a healthy person diagnosed to have TB is 0.001. In a certain city, 1 in 1000 people suffers from TB. A person is selected at random and is diagnosed to have TB. What is the probability that he actually has TB?
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
An item is manufactured by three machines A, B, and C. Out of the total number of items manufactured during a specified period, 50% are manufactured on A, 30% on B, and 20% on C. 2% of the items produced on A and 2% of items produced on B are defective, and 3% of these produced on C are defective. All the items are stored at one godown. One item is drawn at random and is found to be defective. What is the probability that it was manufactured on machine A?
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Let be a discrete random variable whose probability distribution is defined as follows:

This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

The probability distribution of a discrete random variable is given as under:
|
X |
1 |
2 |
4 |
2A |
3A |
5A |
|
P(X) |
1/2 | 1/5 | 3/25 | 1/10 | 1/25 | 1/25 |
Calculate:
The value of if (ii)Variance of X
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

The probability distribution of a discrete random variable is given as under:

This is a Long Answer Type Questions as classified in NCERT Exemplar

A bag contains coins. It is known that of these coins have a head on both sides, while the rest of the coins are fair. A coin is picked at random from the bag and tossed. If the probability that the toss results in a head is , determine the value of .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
Two cards are drawn successively without replacement from a well-shuffled deck of cards. Find the mean and standard deviation of the random variable , where is the number of aces
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:

A die is tossed twice. A ‘success’ is getting an even number on a toss. Find the variance of the number of successes.
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
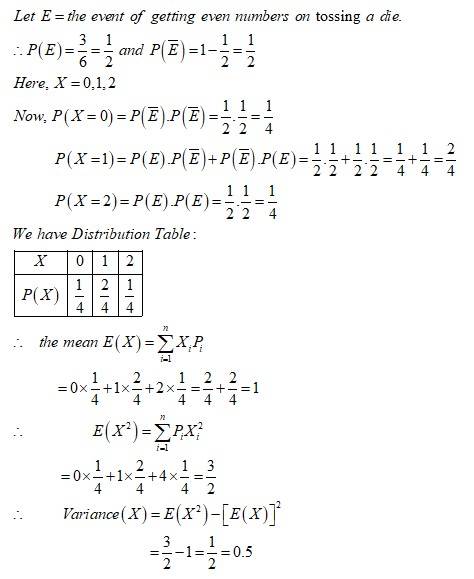
There are 5 cards numbered 1 to 5, one number on each card. Two cards are drawn at random without replacement. Let denote the sum of the numbers on the two cards drawn. Find the mean and variance of .
This is a Long Answer Type Questions as classified in NCERT Exemplar
Sol:
For a loaded die, the probabilities of outcomes are given as under:
and .
The die is thrown two times. Let A and B be the events, ‘same number each time’, and ‘a total score is 10 or more’, respectively. Determine whether or not A and B are independent.
This is a Short Answer Type Questions as classified in NCERT Exemplar

Refer to Exercise 1 above. If the die were fair, determine whether or not the events A and B are independent.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
The probability that at least one of the two events A and B occurs is 0.6. If A and B occur simultaneously with probability 0.3, evaluate ) .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A bag contains 5 red marbles and 3 black marbles. Three marbles are drawn one by one without replacement. What is the probability that at least one of the three marbles drawn be black, if the first marble is red?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Two dice are thrown together and the total score is noted. The events E, F, and G are ‘a total of 4’, ‘a total of 9 or more’, and ‘a total divisible by 5’, respectively.
Calculate , , and and decide which pairs of events, if any, are independent.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Explain why the experiment of tossing a coin three times is said to have binomial distribution.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A and B are two events such that , , and . Find:
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Three events A, B, and C have probabilities , and , respectively. Given that and , find the values of and .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Let and be two independent events such that and .
Describe in words the events whose probabilities are:
This is a Short Answer Type Questions as classified in NCERT Exemplar
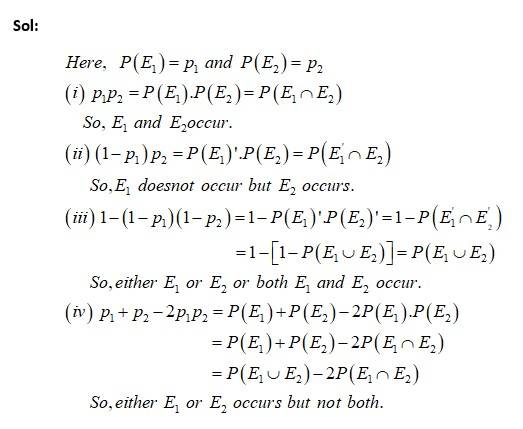
A discrete random variable X has the probability distribution given as below:
|
X |
0.5 |
1 |
1.5 |
2 |
|
P(X) |
k |
k2 |
2k2 |
k |
i. Find the value of k
ii. Determine the mean of the distribution.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Prove that:
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
If X is the number of tails in three tosses of a coin, determine the standard deviation of X.
This is a Short Answer Type Questions as classified in NCERT Exemplar

In a dice game, a player pays a stake of Re1 for each throw of a die. She receives Rs 5 if the die shows a 3, Rs 2 if the die shows a 1 or 6, and nothing otherwise. What is the player’s expected profit per throw over a long series of throws?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

Three dice are thrown at the same time. Find the probability of getting three twos, if it is known that the sum of the numbers on the dice was six.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Suppose 10,000 tickets are sold in a lottery, each for Re 1. First prize is of Rs 3000 and the second prize is of Rs 2000. There are three third prizes of Rs 500 each. If you buy one ticket, what is your expectation?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

A bag contains 4 white and 5 black balls. Another bag contains 9 white and 7 black balls. A ball is transferred from the first bag to the second and then a ball is drawn at random from the second bag. Find the probability that the ball drawn is white.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Bag I contains 3 black and 2 white balls; Bag II contains 2 black and 4 white balls. A bag and a ball are selected at random. Determine the probability of selecting a black ball.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A box has 5 blue and 4 red balls. One ball is drawn at random and not replaced. Its colour is also not noted. Then another ball is drawn at random. What is the probability of the second ball being blue?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Four cards are successively drawn without replacement from a deck of 52 playing cards. What is the probability that all the four cards are kings?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A die is thrown 5 times. Find the probability that an odd number will come up exactly three times.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Ten coins are tossed. What is the probability of getting at least 8 heads?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

The probability of a man hitting a target is 0.25. He shoots 7 times. What is the probability of his hitting at least twice?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, what is the probability that there will be at least one defective watch?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
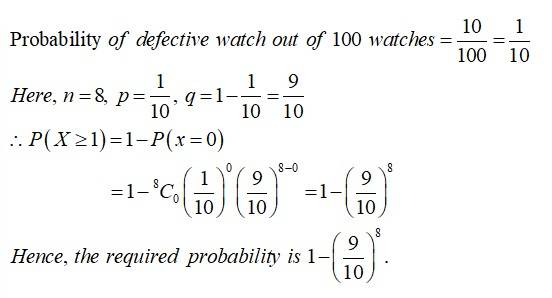
Consider the probability distribution of a random variable X:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P(X) |
0.1 |
0.25 |
0.3 |
0.2 |
0.15 |
Calculate:(i) (ii) Variance of X.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

The probability distribution of a random variable X is given below:
|
X |
0 |
1 |
2 |
3 |
|
P(X) |
k |
i. Determine the value of k.
ii. Determine P and P .
iii. Find .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
For the following probability distribution, determine the standard deviation of the random variable X.
|
X |
2 |
3 |
4 |
|
P(X) |
0.2 |
0.5 |
0.3 |
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
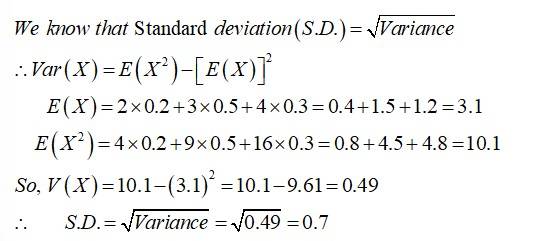
A biased die is such that and other scores being equally likely. The die is tossed twice. If X is the ‘number of fours seen’, find the variance of the random variable X.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

A die is thrown three times. Let X be ‘the number of twos seen’. Find the expectation of X.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Two biased dice are thrown together. For the first die , the other scores being equally likely, while for the second die, and the other scores are equally likely. Find the probability distribution of ‘the number of ones seen’.
This is a Short Answer Type Questions as classified in NCERT
Sol:

Two probability distributions of the discrete random variable X and Y are given below:
|
X |
0 |
1 |
2 |
3 |
|
P(X) |
|
Y |
0 |
1 |
2 |
3 |
|
P(Y) |
Prove that .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

A factory produces bulbs. The probability that any one bulb is defective is and they are packed in boxes of 10. From a single box, find the probability that:
i. one of the bulbs is defective
ii. exactly two bulbs are defective
iii. more than 8 bulbs work properly
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Suppose you have two coins which appear identical in your pocket. You know that one is fair and one is 2-headed. If you take one out, toss it and get a head, what is the probability that it was a fair coin?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Suppose that 6% of the people with blood group O are left-handed and 10% of those with other blood groups are left-handed. 30% of the people have blood group O. If a left-handed person is selected at random, what is the probability that he/she will have blood group O?
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Two natural numbers , are drawn one at a time, without replacement from the set . Find
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Find the probability distribution of the maximum of the two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:

The random variable can take only the values 0, 1, 2. Given that and that , find the value of .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
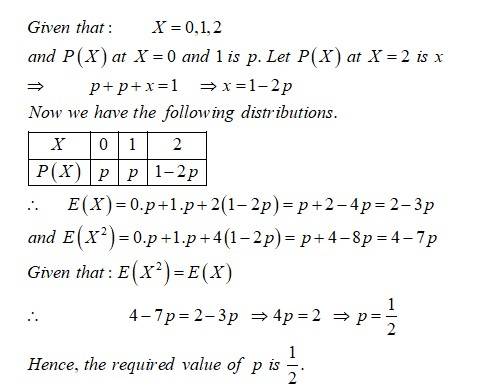
Find the variance of the distribution:
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
P(x) |
1/6 | 5/18 | 2/9 | 1/6 | 1/9 | 1/18 |
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
A and B throw a pair of dice alternately. A wins the game if he gets a total of 6 and B wins if she gets a total of 7. If A starts the game, find the probability of winning the game by A in the third throw of the pair of dice.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Two dice are tossed. Find whether the following two events and are independent: , where denotes a typical sample point.
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
An urn contains white and black balls. A ball is drawn at random and is put back into the urn along with additional balls of the same colour as that of the ball drawn. A ball is again drawn at random. Show that the probability of drawing a white ball now does not depend on .
This is a Short Answer Type Questions as classified in NCERT Exemplar
Sol:
Choose the correct answer from the given four options in each of the Exercises 1 to 38:
Q1. If , and , then is equal to:

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If and , then equals:
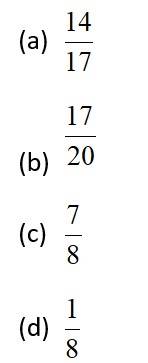
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If , , and , then equals:
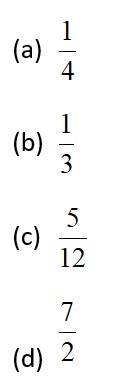
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If , , and , then is equal to:
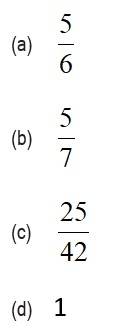
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If A and B are two events such that , , and , then equals:
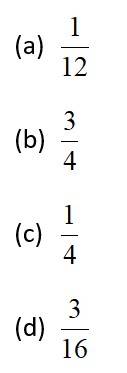
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If , , and , then is equal to:
(a) 0.24
(b) 0.3
(c) 0.48
(d) 0.96
This is a Objective Type Questions as classified in NCERT Exemplar

If and are two events and , , then
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A and B are events such that , , and . Then equals
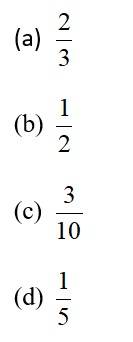
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
You are given that and are two events such that , , and , then equals
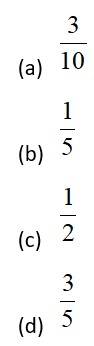
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
In Exercise 64 above, P(B | ) is equal to

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If , , and , then equals:
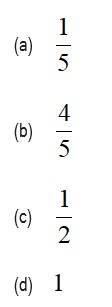
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Let , , and . Then is equal to:
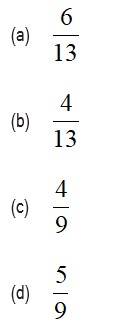
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If and are such events that and , then equals:
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If and are two independent events with and , then equals:
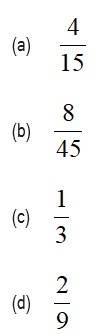
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If two events are independent, then
(a) They must be mutually exclusive
(b) The sum of their probabilities must be equal to 1
(c) (a)and (b) both are correct
(d) None of the above is correct
This is a Objective Type Questions as classified in NCERT Exemplar

Let and be two events such that , , and . Then is equal to:
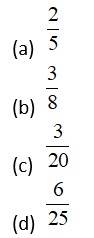
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
If the events and are independent, then is equal to:
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Two events and are independent. If , , then equals:
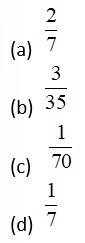
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A bag contains 5 red and 3 blue balls. If 3 balls are drawn at random without replacement, the probability of getting exactly one red ball is
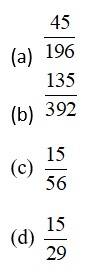
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Refer to Question 74 above. The probability that exactly two of the three balls were red, with the first ball being red, is
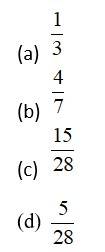
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Three persons, A, B, and C, fire at a target in turn, starting with A. Their probability of hitting the target are 0.4, 0.3, and 0.2 respectively. The probability of exactly two hits is:
(a) 0.024
(b) 0.188
(c) 0.336
(d) 0.452
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Assume that in a family, each child is equally likely to be a boy or a girl. A family with three children is chosen at random. The probability that the eldest child is a girl, given that the family has at least one girl is
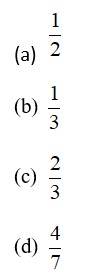
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A die is thrown and a card is selected at random from a deck of 52 playing cards. The probability of getting an even number on the die and a spade card is
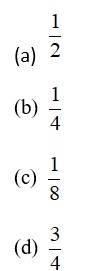
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A box contains 3 orange balls, 3 green balls, and 2 blue balls. Three balls are drawn at random from the box without replacement. The probability of drawing 2 green balls and one blue ball is
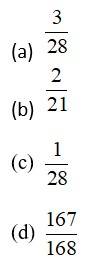
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A flashlight has 8 batteries out of which 3 are dead. If two batteries are selected without replacement and tested, the probability that both are dead is
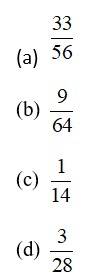
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Eight coins are tossed together. The probability of getting exactly 3 heads is

This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
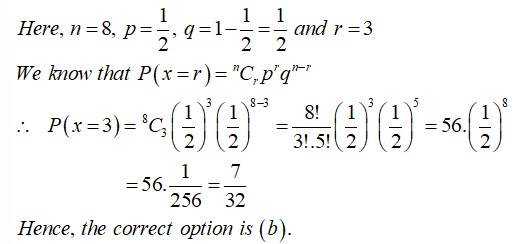
Two dice are thrown. If it is known that the sum of the numbers on the dice was less than 6, the probability of getting a sum of 3, is
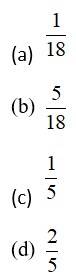
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Which one is not a requirement of a binomial distribution?
(a) There are 2 outcomes for each trial
(b) There is a fixed number of trials
(c) The outcomes must be dependent on each other
(d) The probability of success must be the same for all the trials
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Two cards are drawn from a well-shuffled deck of 52 playing cards with replacement. The probability that both cards are queens is:
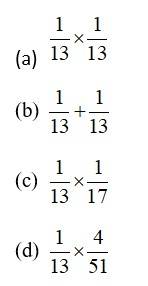
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The probability of guessing correctly at least 8 out of 10 answers on a true-false type examination is
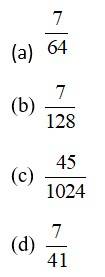
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
The probability that a person is not a swimmer is 0.3. The probability that out of 5 persons, 4 are swimmers is:
(a) 5C4 (0.7)4 (0.3)
(b) 5C1 (0.7) (0.3)4
(c) 5C1 (0.7) (0.3)4
(d) (0.7)4 (0.3)
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:

The probability distribution of a discrete random variable is given below:
: 2 3 4 5
:
The value of is:
(a) 8
(b) 16
(c) 32
(d) 48
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
For the following probability distribution:
: -4 -3 -2 -1 0
: 0.1 0.2 0.3 0.2 0.2
is equal to:
(a) 0
(b) -1
(c) -2
(d) -1.8
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
For the following probability distribution:
: 1 2 3 4
:
is equal to:
(a) 3
(b) 5
(c) 7
(d) 10
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
Suppose a random variable follows the binomial distribution with parameters and , where . If is independent of and , then equals:
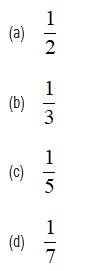
This is a Objective Type Questions as classified in NCERT Exemplar

In a college, 30% of students fail in physics, 25% fail in mathematics, and 10% fail in both. One student is chosen at random. The probability that she fails in physics if she has failed in mathematics is:
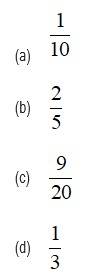
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A and B are two students. Their chances of solving a problem correctly are and , respectively. If the probability of their making a common error is and they obtain the same answer, then the probability of their answer being correct is:
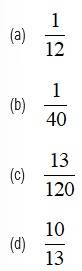
This is a Objective Type Questions as classified in NCERT Exemplar
Sol:
A box has 100 pens of which 10 are defective. What is the probability that out of a sample of 5 pens drawn one by one with replacement, at most one is defective?
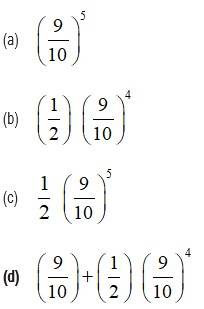
This is a Objective Type Questions as classified in NCERT Exemplar

Let and . Then A and B can be both mutually exclusive and independent.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are independent events, then and are also independent.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are mutually exclusive events, then they will be independent also.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
Two independent events are always mutually exclusive.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are two independent events, then .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
Another name for the mean of a probability distribution is expected value.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are independent events, then .
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are independent, then:
.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are two events such that and , then:
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If , , and are three independent events such that , then:
.
This is a True or False Type Questions as classified in NCERT Exemplar
Sol:
If and are two events such that:
, , , and , then _____
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
If and are such that:
and , then _____
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
If follows binomial distribution with parameters , , and , , then _____
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
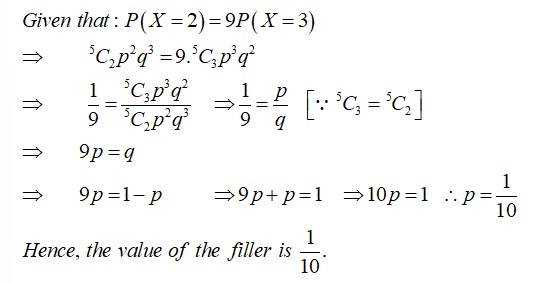
Let be a random variable taking values with probabilities , respectively. Then _____
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
Let and be two events. If , then is _____ of .
This is a Fill in the Blanks Type Questions as classified in NCERT Exemplar
Sol:
JEE Mains Solutions 2022, 26th july , Maths second shift
JEE Mains Solutions 2022, 26th july , Maths, second shift
Commonly asked questions
The minimum value of the sume of the squares of the roots of x2 + (3 – a)x + 1 = 2a is
Let a and b be the roots of the equation
Therefore a + b = a – 3, ab = 1 – 2a Þ a2 + b2 = (a – 3)2 – 2 (1 – 2a) = a2 – 6a + 9 – 2 + 4a = a2 – 2a + 7 = (a – 1)2 + 6 Þ So,
If z = x + iy satisfies
So, z lies on perpendicular bisector of (0, 1) and (0, 5) i.e., line y = 2 as |z| = 2 z = 2i x = 0 and y = 2 so, x + 2y + 4 = 0
Let A = and B = , then the value of A’BA is:
Kindly consider the following equation
Let P and Q be any points on the curves (x – 1)2 + (y + 1)2 = 1 and y = x2, respectively. The distance between P and Q is minimum for some vale of the abscissa of P in the interval
Let equation of normal to x2 = y at Q (t, t2) is x + 2ty = t + 2t3
It passes through the point (1, -1) so, 2t3 + 3t – 1 = 0
Let f(t) = 2t3 + 3t – 1 f
Let P(1 – sin q, -1 + cos q) slope of normal = slope of CP Þ = tan q according to question ,
Þ g’(t) < 0 Þ g(t) is decreasing function in
If the maximum value of a, for which the function fa(x) = tan-1 2x – 3ax + 7 is non-decreasing in , is , then is equal to
Let = for some Then the value of α + β is:
The value of
dx is equal to
= 20 (p + 2)
Le the solution curve y = f(x) of the differential equation pass through the origin. Then is equal to
Solution of differential equation is
Curve is passing through origin, c = 0
The acute angle between the pair of tangents drawn to the ellipse 2x2 + 3y2 = 5 from the point (1, 3) is
Equation of tangent having slope m is
which passes through (1, 3) and we get m1 + m2 = -4 and m1m2 =
Acute angle between the tangents is α = tan-1
The equation of a common tangent to the parabolas y = x2 and y = -(x – 2)2 is
Equation of tangent of slope m to y = x2 is y = mx -
Equation of tangent of slope m to y = - (x - 2)2 is y = m (x – 2) +
If both equation represent the same line therefore on comparing (i) and (ii) we get m = 0, 4
therefore equation of tangent is y = 4x – 4
Let the abscissae of two points P and Q on a circle be the roots of x2 – 4x – 6 = 0 and the ordinates of P and Q be the roots of y2 + 2y – 7 = 0. If PQ is a diameter of the circle x2 + y2 + 2ax + 2by + c = 0, then the value of (a + b +) is……………
Abscissae of PQ are roots of x2 – 4x – 6 = 0
Ordinates of PQ are roots of y2 + 2y – 7 = 0 and PQ is diameter
Equation of circle is
But, given
By comparison a = -2, b = 1, c = -13 Þ a + b – c = -2 + 1 + 13 = 12
If the line x – 1 = 0 is a directrix of the hyperbola kx2 – y2 = 6, then the hyperbola passes through the point
Given hyperbola : so eccentricity e = and directrices
k = 2 therefore equation of hyperbola is
hence it passes through the point
A vector is parallel to the line of intersection of the plane determined by the vectors and the plane determined by the vectors The obtuse angle between and the vector is
is a vector normal to the plane determined by
is a vector normal to the pane determined by and then =
Vector is parallel to i.e. is parallel to
Given
consine of acute angle between =
obtuse angle between
If 0 < x < and then a value of sin is
Now
Negation of the Boolean expression p is
Let X be a binomially distributed random variable with mean 4 and variance Then, is equal to
Mean = 4 = = np
Variance =
The integral
The area bounded by the curves y = and y = 1 is
Let A = {1,2,3,4,5,6,7} and B = {3,6,7,9}. Then the number of elements in the set
If C is formed only by {1, 2, 4, 5} total number of subsets of A = 27.
Total number of subsets of {1, 2, 4, 5} = 24
Number of subsets where
= 27 – 24 = 112
The largest value of a, for which the perpendicular distance of the plane containing the lines from the point (2,1,4 is , is………
The normal vector to the plane is
(1 – a)x + y + z = 2 – a …… (i)
Now distance from (2, 1, 4) =
the largest value of a = 2.
Numbers are to be formed between 1000 and 3000, which are divisible by 4, using the digits 1,2,3,4,5 and 6 without repetition of digits. Then the total number of such numbers is………
Last two digit must be in form
Total number of required number = 12 + 18 = 30
where m and n are co-prime, then m + n is equal to……..
If the sum of solutions of system of equations 2sin2q - cos2q = 0 and 2 cos2q + 3sinq = 0 in the interval [0, 2p] is kp, then k is equal to……..
The mean and standard deviation of 40 observations are 30 and 5 respectively. It was noticed that two of these observations 12 and 10 were wrongly recorded. If is the standard deviation of the data after omitting the two wrong observations from the data, then is equal to………
………. (i)
after omitting two wrong observations
The plane passing through the line L : and perpendicular to the plane 3x + 2y + z = 6 is 3x 8y + 7z = 4. If is the acute angle between the line L and the y-axis, then 415 cos2 is equal to……….
plane containing the line P : 3x – 8y + 7z = 4
If be vector parallel to L.
then as P containing the line
If be the acute angle between line L & Y axis then cos =
Suppose y = y(x) be the solution curve to the differential equation such that is finite. If a and b are respectively the x and y intercepts of the tangent to the curve at x = 0, then the value of a 4b is equal to…………
soln
as for x y finite c = 0
Different A.P’s are constructed with the first term 100, the last term 199 and integral common differences. The sum of the common differences of all such A.P.’s having at least 3 terms and at most 33 terms is……..
sum of common differences = 33 + 11 + 9 = 53
The number of matrices A = where a, b, c, d such that A = A1, is……..
A =
a2 + bc = bc + d2 = 1 ………. (i)
and b (a + d) = c (a + d) = 0 ……… (ii)
Case 1
b = c = 0
then possible ordered pair of
(a, d) (1, 1) (-1, -1) (-1, 1) (1, -1) total 4 possible case
Case 2
a = -d
then (a, d) (-1, 1) (1, -1)
then bc = 0
now if b = 0
then possible choice for {-1, 0, 1, 2, …….10} = 12
Similarly if c = 0 then possible choice for is = 12
but (0, 0) counted twice
bc = 0 in (12 + 12 – 1) = 23 ways
total number of ways = 2 × 23 = 46
total number of required matrices = 46 + 4 = 50
27th July 2022 first shift
27th July 2022 first shift
Commonly asked questions
For let the solutions of the equation =, 0 < be and , where the inverse trigonometric functions take only principal values. If the solutions of the equation x2 – bx – 5 = 0 are is equal to
use
Sum of roots b = 1 + 2
Product of roots 5 = 2
b = 4, k2 =
The mean and variance of 10 observations were calculated as 15 and 15 respectively by a student who took by mistake 25 instead of 15 for one observation. Then, the correct standard deviation is
Actual mean
Actual variance =
Let the line intersect the plane containing the lines and 4ax – y + 5z – 7a = 0 = 2x – 5y – z – 3, a at the point Then the value of + + equals
Plane through 4ax – y + 5z – 7a = 0 = 2x – 5y – z – 3
is
This plane contains 4, -1, 0
9a + 1 + 10 = 0…… (i)
Plane contains the line
……. (ii)
From (i) & (ii) a = 1, =1
Equation of plane
An ellipse passes through the vertices of the hyperbola Let the major and minor axes of the ellipse E coincide with transverse and conjugate axes of the hyperbola H, respectively. Let the product of the eccentricities of E and H be If is the length of the latus rectum of the ellipse E, then the value of 113 is equal to
Let y = y(x) be the solution curve of the differential equation which passes through the point . Then is equal to
Integrate
calculate C.
Let M and N be the number of points on the curve y5 – 9xy + 2x = 0, where the tangents to the curve are parallel to x-axis and y-axis, respectively. Then the value of M + N equals
y5 – 9xy + 2x = 0
differentiate 5y4 – 9x 9y + 2 = 0
For horizontal tangent which does not satisfy the equation so no horizontal
For vertical tangent
m = 0, N = 2
Let f(x) = 2x2 – x – 1 and Then, the value of is equal to
= 10620
Let S be the set containing all 3 × 3 matrices with entries from . The total number of matrices such that the sum of all the diagonal elements of ATA is 6 is
Let A =
Now ATA
trace will be
total ways = 9C6.26.1.1.1 = 5376
If the length of the latus rectum of the ellipse x2 + 4y2 + 2x + 3y is 4, and is the length of the its major axis, then is equal to
length of latus rectum =
Major axis =
Let S Then is equal to
take z = x + iy
if y = 0 x = 0, 1
Maths NCERT Exemplar Solutions Class 12th Chapter Thirteen Exam