- Mechanical Properties of Fluids Questions and Answers
- 28th June 2022 (First Shift)
- JEE MAINS 26th February 2021 (First Shift)
- JEE Mains 2020
Mechanical Properties of Fluids Questions and Answers
| 1. (a) Pressure decreases as one ascends the atmosphere. If the density of air is ρ, what is the change in pressure dp over a differential height dh? (b) Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the surface of the earth is p0. (c) If Po = 1.03×105 N m-2, ρo = 1.29 kg m-3 and g = 9.8 m s-2, at what height will the pressure drop to (1/10) the value at the surface of the earth? (d) This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model. |
| Explanation-(a) Consider a horizontal parcel of air with cross section A and height dh Let the pressure on the top surface and bottom surface be P and p+dp. If the parcel is in equilibrium , then the net upward force must be balanced by the weight (P+dP)-PA=- dP= - negative sign shows that pressure decreases with height. (b) Let o be the density of air on the surface of earth. As per question , pressure density
dP= -
In P=Poe(- ) (c) As P =Po in p=1/10 Po in( ) =- in1/10 =- h=- in1/10= - -1= = = = 16 103m (d) We know that P , temperature remains constant only near the surface of the earth , not at greater heights. |
| 2. Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg-1, the mechanical equivalent of heat J = 4.2 J cal-1, density of water ρw = 103 kg/m3, Avagadro’s No NA = 6.0 × 1026 k mole-1 and the molecular weight of water MA = 18 kg for 1 k mole. (a) Estimate the energy required for one molecule of water to evaporate. (b) Show that the inter–molecular distance for water is d= and find its value. (c) 1 g of water in the vapor state at 1 atm occupies 1601cm3. Estimate the intermolecular distance at boiling point, in the vapour state. (d) During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d′. Estimate the value of F. (e) Calculate F/d, which is a measure of the surface tension. |
| Explanation-(a) Lv=540 kcal kg-1 = 540 kg-1 = 540 4.2jkg-1 Energy required to evaporate 1kg of water = Lv kcal And MA kg of water requires MALV kcal Since there are NA molecules in MA kg of water the energy required for 1 molecule to evaporate Is U= = =90 = 6.8 (b) Let the water molecules to be points and are separated at a distance d from each other volume of NA molecule of water = thus the volume of one molecule is = the volume around one molecule is d3= d= d= 3.1 (c) 1 kg of vapour occupies volume =1601 m3 18 kg of vapour occupies 18 m3 6 molecules occupies 18 m3 1 molecule occupies = 18 /6 If d is the inter molecular distance then m3 d1= (30 1/3 = 36.3 m (d) Work done to change the distance from d to d1 is = F(d1-d) this work done is equal to energy required to evaporate 1 molecule F(d1-d)=6.8 F= = = 2.05 (e) surface tension =f/d= |
| 3. A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K-1, 1 atm. = 1.013×105 Pa; the membrane tension is 5 N m-1.) |
| Explanation- Let the pressure inside the ballon be P1 and the outside pressure be Po, then excess pressure is Pi-Po =2S/r Considering the air to be an ideal gas piV = niRTi = where, V is the volume of the air inside the balloon, ni is the number of moles inside and Ti is the temperature inside, and poV =noRTo where V is the volume of the air displaced and no is the number of moles displaced and To is the temperature outside. So ni= Where Mi is the mass of air inside and MA is the molar mass of air no= if w Is the load it can raise then w+M1g=Mog as atmosphere 21% O2 and 79%N2 is present so molar mass of air Mi=0.21 = 28.84g So weight raised by the ballon w=(Mo-Mi)g = = 3044.2N Mass lifted by the ballon =w/g =3044.2/10=304.42kg So approximately 305 kg |
Commonly asked questions
(a) Pressure decreases as one ascends the atmosphere. If the density of air is ρ, what is the change in pressure dp over a differential height dh?
(b) Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the surface of the earth is p0.
(c) If Po = 1.03×105 N m-2, ρo = 1.29 kg m-3 and g = 9.8 m s-2, at what height will the pressure drop to (1/10) the value at the surface of the earth?
(d) This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.
This is a long answer type question as classified in NCERT Exemplar
(a) consider a horizontal parcel of air with cross section A and height dh
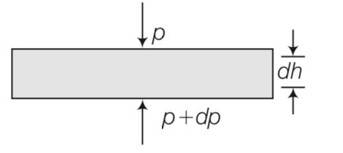
Let the pressure on the top surface and bottom surface be P and p+dp. If the parcel is in equilibrium , then the net upward force must be balanced by the weight
(P+dP)-PA=-
dP= -
negative sign shows that pressure decreases with height.
(b) let o be the density of air on the surface of earth.
As per question , pressure density
dP= -
In
P=Poe(- )
(c) as P =Po
in
p=1/10 Po
in( ) =-
in1/10 =-
h=- in1/10= - -1=
=
=
= 16 103m
(d) we know that
P , temperature remains constant only near the surface of the earth , not at greater heights.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg-1, the mechanical equivalent of heat J = 4.2 J cal-1, density of water ρw = 103 kg/m3, Avagadro’s No NA = 6.0 × 1026 k mole-1 and the molecular weight of water MA = 18 kg for 1 k mole.
(a) Estimate the energy required for one molecule of water to evaporate.
(b) Show that the inter–molecular distance for water is d= and find its value.
(c) 1 g of water in the vapor state at 1 atm occupies 1601cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
(d) During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d′. Estimate the value of F.
(e) Calculate F/d, which is a measure of the surface tension.
This is a long answer type question as classified in NCERT Exemplar
(a) Lv=540 kcal kg-1
= 540 kg-1 = 540 4.2jkg-1
Energy required to evaporate 1kg of water = Lv kcal
And MA kg of water requires MALV kcal
Since there are NA molecules in MA kg of water the energy required for 1 molecule to evaporate
Is
U=
=
=90
= 6.8
(b) Let the water molecules to be points and are separated at a distance d from each other
volume of NA molecule of water =
thus the volume of one molecule is =
the volume around one molecule is d3=
d=
d= 3.1
(c) 1 kg of vapour occupies volume =1601 m3
18 kg of vapour occupies 18 m3
6 molecules occupies 18 m3
1 molecule occupies = 18 /6
If d is the inter molecular distance then
m3
d1= (30 1/3
= 36.3 m
(d) Work done to change the distance from d to d1 is = F(d1-d)
this work done is equal to energy required to evaporate 1 molecule
F(d1-d)=6.8
F=
=
= 2.05
(e) Surface tension =f/d=
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K-1, 1 atm. = 1.013×105 Pa; the membrane tension is 5 N m-1.)
This is a long answer type question as classified in NCERT Exemplar
Let the pressure inside the ballon be P1 and the outside pressure be Po, then excess pressure is Pi-Po =2S/r
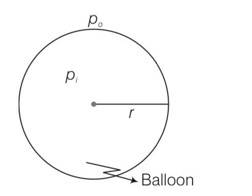
Considering the air to be an ideal gas piV = niRTi = where, V is the volume of the air inside the balloon, ni is the number of moles inside and Ti is the temperature inside, and poV =noRTo where V is the volume of the air displaced and no is the number of moles displaced and To is the temperature outside.
So ni=
Where Mi is the mass of air inside and MA is the molar mass of air
no=
if w Is the load it can raise then w+M1g=Mog
as atmosphere 21% O2 and 79%N2 is present
so molar mass of air
Mi=0.21 = 28.84g
So weight raised by the ballon
w=(Mo-Mi)g
=
= 3044.2N
Mass lifted by the ballon =w/g =3044.2/10=304.42kg
So approximately 305kg
Is viscosity a vector?
This is a short answer type question as classified in NCERT Exemplar
Viscosity is a property of liquid it does not have any direction hence it is scalar quantity.
Is surface tension a vector?
This is a short answer type question as classified in NCERT Exemplar
No surface tension is a scalar quantity.
Surface tension = work done/ surface area, where work done and surface area both are scalar quantities.
Iceberg floats in water with part of it submerged. What is the fraction of the volume of iceberg submerged if the density of ice is i = 0.917 g cm-3 ?
This is a short answer type question as classified in NCERT Exemplar
Given density of ice i = 0.917 g cm-3
Density of water 3
Let V be the total volume of iceberg and V’ of its volume be submerged in water.
In floating condition
Weight of the iceberg= weight of the water displaced by the submerged part by ice
V ig = V’ g
=
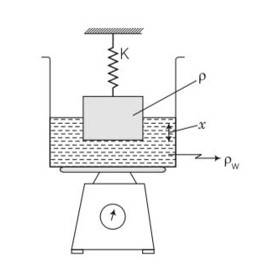
A vessel filled with water is kept on a weighing pan and the scale adjusted to zero. A block of mass M and density ρ is suspended by a massless spring of spring constant k. This block is submerged inside into the water in the vessel. What is the reading of the scale?
This is a short answer type question as classified in NCERT Exemplar
Consider the diagram,
The scale is adjusted to zero, therefore, when the block suspended to a spring is immersed
In water, then the reading of the scale will be equal to the thrust on the block due to water.
Thrust= weight of water displaced
=V wg (where V is volume of the block and w is density of water)
= =
A cubical block of density ρ is floating on the surface of water. Out of its height L, fraction x is submerged in water. The vessel is in an elevator accelerating upward with acceleration a . What is the fraction immersed?
This is a short answer type question as classified in NCERT Exemplar
Consider the diagram.
Let the density of water be and a cubical block of ice of side L be floating in water with x of its height L submerged in water.
Volume of the block V = L3
Mass of the block m = V =L3
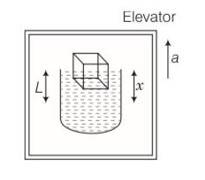
Weight of the block = mg= L3
1st case
Volume of the water displaced by the submerged part of the block= xL2
Weight of the water displaced by the block
In floating condition, x L2
Weight of the block= Weight of the water displaced by the block
L3 = xL2
2nd case
When elevator is accelerating upward with an acceleration a, then effective acceleration
= (g+a)
Then, weight of the block =m (g+a)
= L3 (g+a)
Let x1 fraction be submerged in water when elevator is accelerating upwards.
Now, in the floating condition, weight of the block= weight of the displaced water
L3 )= ( 2) (g+a)
= x
From1st and 2nd case,
We see that, the fraction of the block submerged in water is independent of the acceleration of the elevator.
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5×10-5 m. The surface tension of sap is T = 7.28×10-2Nm-1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
This is a short answer type question as classified in NCERT Exemplar
Given radius r= 2.5
Surface tension S= 7.28
Angle of contact = 00
The maximum height to which SAP can rise in trees through capillarity action is given by
h = where S = surface tension, = density, r= radius
h=
This is the maximum height to which the SAP can rise due to surface tension. Since, many trees have heights much more than this, capillary action alone cannot account for the rise of water in all trees.
The free surface of oil in a tanker, at rest, is horizontal. If the tanker starts accelerating the free surface will be titled by an angle θ. If the acceleration is a m s–2, what will be the slope of the free surface?
This is a short answer type question as classified in NCERT Exemplar
Consider the diagram where a tanker is accelerating with acceleration a.
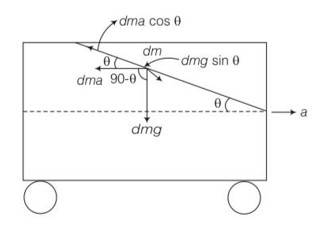
Consider an elementary particle of the fluid of mass dm.
The acting forces on the particle with respect to the tanker are shown above.
Now, balancing forces (as the particle is in equilibrium) along the inclined direction
component of weight= component of pseudo force dmg sin =dma cos (we have assumed that the surface is inclined at an angle q) where, dma is pseudo force
g sin =acos
a=g tan
tan = a/g = slope
Two mercury droplets of radii 0.1 cm. and 0.2 cm. collapse into one single drop. What amount of energy is released? The surface tension of mercury T= 435.5 × 10-3 Nm-1 .
This is a short answer type question as classified in NCERT Exemplar
Consider the diagram
Radii of mercury droplets r1=0.1cm = 1
r2=0.2cm=2
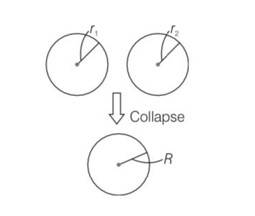
Surface tension T= 435.5 × 10-3 Nm-1
Let the radius of the big drop formed by collapsing be R
Therefore,
volume of big drop = volume of small droplets
4/3 R3=4/3 4/3
R3=
= 0.13+0.23
= 0.001+0.008
=0.009
R= 0.21 cm = 2.1
Change in surface area = 4
=4
Energy released =T
= T
= 435.5 2-(1 )
= 435.5
= -32.23
Therefore -3.22 energy will be absorbed.
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
This is a short answer type question as classified in NCERT Exemplar
When a big drop of radius R, breaks into N droplets each of radius r, the volume remains constant.
Volume of big drop = N volume of each small drop
R3 =Nr3
N=R3/r3
Now change in surface area = 4 -N4 r2
= 4
Energy released = T = S
Due to releasing of this energy , the temperature is lowered.
If is the density and s is specific heat of liquid and its temperature is lowered by , then energy released = ms
T ( )=
=
=
=
The surface tension and vapour pressure of water at 20°C is 7.28×10-2 Nm-1 and 2.33×103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
This is a short answer type question as classified in NCERT Exemplar
Surface tension of water S= 7.28×10-2 Nm-1
Vapour pressure p= 2.33×103 Pa
The drop will evaporate, if the water pressure is greater than the vapour pressure.
Let a water droplet or radius R can be formed without evaporating.
Vapour pressure= Excess pressure in drop.
P=2S/R
R= 2S/P=
A tall cylinder is filled with viscous oil. A round pebble is dropped from the top with zero initial velocity. From the plot shown in Fig, indicate the one that represents the velocity (v) of the pebble as a function of time (t)
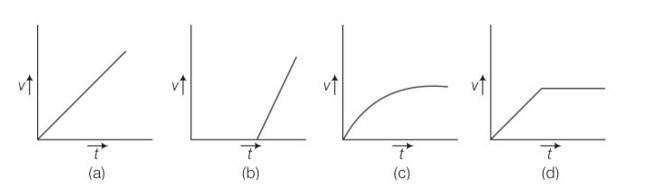
This is a multiple choice answer as classified in NCERT Exemplar
(c) When the pebble is falling through the viscous oil the viscous force is
F=6
where r is radius of the pebble, v is instantaneous speed, his coefficient of viscosity. As the force is variable, hence acceleration is also variable so v-t graph will not be straight line. First velocity increases and then becomes constant known as terminal velocity.
Which of the following diagrams (Fig.) does not represent a streamline flow?
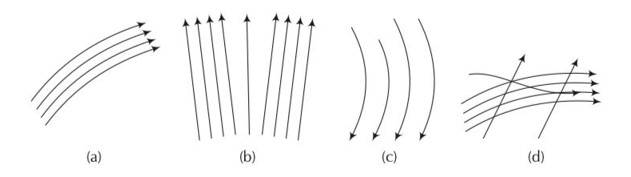
This is a multiple choice answer as classified in NCERT Exemplar
(d) In a streamline flow at any given point, the velocity of each passing fluid particles remains constant. If we consider a cross-sectional area, then a point on the area cannot have different velocities at the same time, hence two streamlines of flow cannot cross each other.
Along a streamline
(a) The velocity of a fluid particle remains constant
(b) The velocity of all fluid particles crossing a given position is constant
(c) The velocity of all fluid particles at a given instant is constant
(d) The speed of a fluid particle remains constant
This is a multiple choice answer as classified in NCERT Exemplar
(b) As we know for a streamline flow of a liquid velocity of each particle at a particular cross-section is constant, because Av = constant (law of continuity) between two cross-section of a tube of flow.
An ideal fluid flows through a pipe of circular cross-section made of two sections with diameters 2.5 cm and 3.75 cm. The ratio of the velocities in the two pipes is
(a) 9:4
(b) 3:2
(c)
(d)
This is a multiple choice answer as classified in NCERT Exemplar
(a) d1= diameter at 1st point is 2.5

d2= diameter at 2nd point is 3.75
Applying equation of continuity for cross section A1 and A2
A1V1=A2V2
2
= =
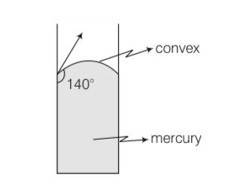
The angle of contact at the interface of water-glass is 0°, Ethyl alcohol-glass is 0°, Mercury-glass is 140° and Methyl iodide glass is 30°. A glass capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is
(a) Water
(b) Ethyl alcohol
(c) Mercury
(d) Methyl iodide.
This is a multiple choice answer as classified in NCERT Exemplar
(c) According to the question, the observed meniscus is of convex figure shape. Which is only possible when angle of contact is obtuse. Hence, the combination will be of mercury-glass (140°)
For a surface molecule
(a) The net force on it is zero
(b) There is a net downward force
(c) The potential energy is less than that of a molecule inside
(d) The potential energy is more than that of a molecule inside
This is a multiple choice answer as classified in NCERT Exemplar
(b), (d) Consider the diagram where two molecules of a liquid are shown. One is well inside the liquid and other is on the surface. The molecule (A) which is well inside experiences equal forces from all directions, hence net force on it will be zero.
And molecules on the liquid surface have some extra energy as it surrounded by Only lower half side of liquid molecules.
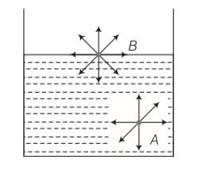
Pressure is a scalar quantity because
(a) It is the ratio of force to area and both force and area are vectors
(b) It is the ratio of the magnitude of the force to area
(c) It is the ratio of the component of the force normal to the area
(d) It does not depend on the size of the area chosen
This is a multiple choice answer as classified in NCERT Exemplar
(b), (c) Pressure is defined as the ratio of magnitude of component of the force normal to the area and the area under consideration.
As magnitude of component is considered, hence, it will not have any direction. So, Pressure is a scalar quantity.
A wooden block with a coin placed on its top, floats in water as shown in Fig.
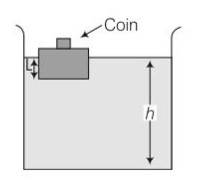
The distance l and h are shown in the figure. After some time the coin falls into the water. Then
(a) l decreases
(b) h decreases
(c) l increases
(d) h increase
This is a multiple choice answer as classified in NCERT Exemplar
(a), (b) When the coin falls into the water, weight of the (block + coin) system decreases, which was balanced by the upthrust force earlier. As weight of the system decreases, hence upthrust force will also decrease which is only possible when l decreases.
As l decreases volume of water displaced by the block decreases, hence h decreases. As the coin falls into water, it displaces some volume of water which is very less. Hence, we neglect volume of the coin.
With increase in temperature, the viscosity of
(a) Gases decreases
(b) Liquids increases
(c) Gases increases
(d) Liquids decreases
This is a multiple choice answer as classified in NCERT Exemplar
(c), (d) For liquids coefficient of viscosity
i.e with increase in temperature decreases.
For gases coefficient of viscosity
i.e with increase in temperature decreases.
Streamline flow is more likely for liquids with
(a) High density
(b) High viscosity
(c) Low density
(d) Low viscosity
This is a multiple choice answer as classified in NCERT Exemplar
(b), (c) Streamline flow is more likely for liquids having low density. We know that greater the coefficient of viscosity of a liquid more will be velocity gradient hence each line of flow can be easily differentiated. Also higher the coefficient of viscosity lower will be Reynolds number, hence flow more like to be streamline.
28th June 2022 (First Shift)
28th June 2022 (First Shift)
Commonly asked questions
Motion of a particle in x – y plane is described by a set of following equations x = 4sin m and y = 4sin The path of a particle will be
- (i)
- (ii)
From (i) and (ii) cos2
Two planets A and B of equal mass are having their period of revolutions TA and TB such that TA = 2TB. These planets are revolving in the circular orbits or radii rA and rB respectively. Which out of the following would be the correct relationship of their orbits?
According to kepler’s third law of time period –
Given below are two statements:
Statement – I : When moment of an ideal gas undergoes adiabatic change from state to state then work done is w = where R = universal gas constant.
Statement – II : In the above case, when work done on the gas, the temperature of the gas would rise.
Choose the correct answer from the options given below:
In case of adiabatic process
for adiabatic process :-
So, when work is done by the gas, temperature decreases and when work is done on the gas, temperature rises.
Given below are two statements:
Statement – I : A point change is brought in an electric field. The value of electric field at a point near to the change may increase if the charge is positive.
Statement – I : An electric dipole is placed in a non-uniform electric field. The net electric force on the dipole will not be zero.
Choose the correct answer from the options given below:
The aperture of the objective is 24.4 cm. The resolving power of this telescope, if a alight of wavelength 2440 is used to see the object will be
Resolving power, =
THE de Broglie wavelength for an electron and a photon are respectively. For the same kinetic energy of electron and photon, which of the following presents the correct relation between the de Broglie wavelengths of two
- (ii)
Ke = KP
For using a multimeter to identify diode from electrical compounds, choose the correct statement out of the following about the diode
Diode conducts current only in one direction.
The velocity of sound in a gas, in which two wavelengths 4.08m and 4.16m produce 40 beats in 12s, will be
An AC source is connected to an inductance of 100 mH, a capacitance of 100 and a resistance of 120 as shown in figure. The time in which the resistance having a thermal capacity 2 J/°C will get heated by 16°C is________ s.
= 150
The total internal energy of two mole mono atomic ideal gas at temperature T = 300K will be __________J. (Given R = 8.31 J/mol.K)
A telegraph line of length 100km has a capacity of and it carries an alternating current at 0.5 kilo cycle per second. If minimum impedance is required, then the value of the inductance that need to be introduced in series is _________mH. (if π = )
C = 10-6 f
f = 0.5 × 103 = 500
for minimum impedance :
xL = xC
Given below are two statements : One is labeled as Assertion A and the other is labeled as Reason R.
Assertion A : Product of Pressure (P) and time (t) has the same dimension as that of coefficient of viscosity.
Reason R : Coefficient of viscosity =
Choose the correct answer from the options given below:
Pressure × time
Coefficient of viscosity,
A particle of mass m is moving in a circular path of constant radius r such that its centripetal acceleration (a) is varying with time t as a = k2 rt2, where k is a constant. The power delivered to the particle by the force acting on it is given as
a = k2rt2
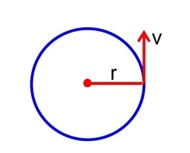
⇒ tangential force, Ft = mat = mkr
Note → Power delivered by centripetal force will be zero.
Match List – I with List – II
|
|
List – I |
|
List – II |
|
A. |
Moment of inertia of solid sphere of radius R about and tangent. |
I. |
5/3MR2 |
|
B. |
Moment of inertia of hollow sphere of radius (R) about any tanget |
II. |
7/5MR2 |
|
C. |
Moment of inertia of circular ring of radius (R) about its diameter. |
III. |
1/4MR2 |
|
D. |
Moment of inertial of circular disc of radius (R) about any diameter. |
IV. |
1/2MR2 |
Choose the correct answer from the options given below:
Use formula for M.I.
A water drop of diameter 2 cm is broken into 64 equal droplets. The surface tension of water is 0.075N/m. In this process the gain in surface energy will be
Gain in surface energy,
from volume centenary,
Initial surface area, Ai = 4pR2
final surface area,
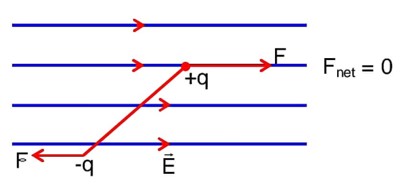
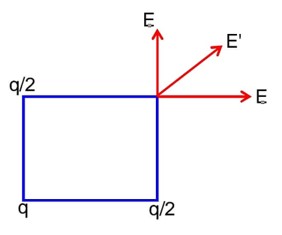
The three charges q/2, q and q/2 are placed at the corners A, B and C of a square of side ‘a’ as shown in figure. The magnitude of electric field (E) at the corner D of the square, is
A radar sends an electromagnetic single of electric (E0) = 2.25 V/m and magnetic field (B0) = 1.5 × 10-8 T which strikes a target on line of sight at a distance of 3km in a medium. After that, a part of signal (echo) reflects back towards the radar with same velocity and by same path. If the signal was transmitted at time t = 0 from radar, then after how much time echo will reach to the radar?
Speed of declromagnetic signal,
Time to reach each to the same
radar,
The refracting angle of a prims is A and refractive index of the material of the prism is cot (A/2). Then the angle of minimum deviation will be
At minimum deviation –
Using snell’s low : -
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, Kp are related as
X + p → Y + b
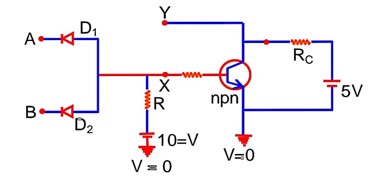
In the following circuit, the correct relation between output (Y) and inputs A and B will be
From Truth table .
Given below are two statements : One is labeled as Assertion A and the other is labeled as Reason R.
Assertion A : n-p-n transistor permits more current that a p-n-p transistor.
Reason R : Electrons have greater mobility as a change carrier.
Choose the correct answer form the options given below
Using factual data.
Match List – I with List – II
|
|
List – I |
|
List – II |
|
A. |
Television signal |
I. |
03 KHz |
|
B. |
Radio signal |
II. |
20 KHz |
|
C. |
High Quality Music |
III. |
02 MHz |
|
D. |
Human speech |
IV. |
06 MHz |
Choose the correct answer from the options given below:
Using factual data.
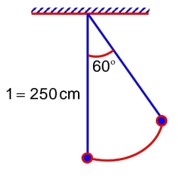
A pendulum is suspended by a string of length 250 cm. The mass of the bob of the pendulum is 200g. The bob is pulled aside until the string is at 60° with vertical as shown in the figure. After releasing the bob, the maximum velocity attained by the bob will be_________ ms-1. (if g = 10m/s2)
From conservation of Energy:

The position vector of 1kg object is and its velocity The magnitude of is angular momentum is where x is________.
=
=√=√91
A man of 60kg is running on the road and suddenly jumps into stationary trolly car of mass 120kg. Then, the trolly car starts moving with velocity 2ms-1. The velocity of the running man was _________ ms-1, when he jumps into the car
Using conservation of momentum:
60 × v = (60 + 120) × 2
⇒ v = 6m/s
A hanging mass M is connected to a four times bigger mass by using a string-pulley arrangement, as shown in the figure. The bigger mass is placed on a horizontal ice-slab and being pulled by 2 Mg force. In this situation, tension in the string is for x_________. Neglect mass of the string and fiction of the block (bigger mass) with ice slab.
Using newton’s law:
2mg – T = 4ma - (1)
T – mg = ma - (2)
From (1) & (2) :
A singly ionized magnesium atom (A = 24) ion is accelerated to kinetic energy 5 ke V, and is projected perpendicularly into a magnetic field B of the magnitude 0.5 T. The radius of path formed will be ________cm.
=
= 9.975 × 102 cm
= 9.975 cm
JEE MAINS 26th February 2021 (First Shift)
JEE MAINS 26th February 2021 (First Shift)
Commonly asked questions
A container is divided into two chambers by a partition. The volume of first chamber is 4.5 litre and second chamber is 5.5 litre. The first chamber contain 3.0 moles of gas at pressure 2.0 atm and second chamber contains 4.0 moles of gas at pressure 3.0 atm. After the partition is removed and the mixture attains equilibrium, then, the common equilibrium pressure existing in the mixture is x × 10-1 atm. Value of x is----------.
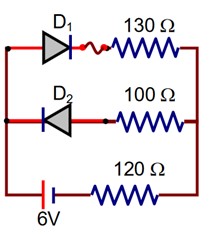
The circuit contains two diodes each with a forward resistance of 50 and with infinite reverse resistance. If the battery voltage is 6 V, the current through the 120 resistance is---------mA.
D1 is forward biased & D2 is reverse biased.
In an electrical circuit, a battery is connected to pass 20 C of charge through it in a certain given time. The potential difference between two plates of the battery is maintained at 15V. The work done by the battery is--------- J.
The maximum and minimum amplitude of an amplitude modulated wave is 16V and 8V respectively. The modulation index for this amplitude wave x × 10-2. The value of x is----------.
Modulation Index
A boy pushes a box of mass 2kg with a force on a frictionless surface. If the box was initially at rest, then-------------m is displacement along the x – axis after 10s.
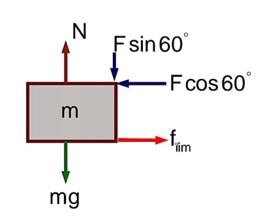
As shown in the figure, a block of mass is kept on a horizontal rough surface of coefficient of friction The critical force to be applied on the vertical surface as shown at an angle 60° with horizontal such that it does not move, will be 3x. The value of x will be-------------.
[g = 10m/s2 ; sin 60° = cos60° =
N = mg + F sin 60°
In a series LCR resonant circuit, the quality factor is measured as 100. If the inductance is increased by two fold and resistance is decreased by two fold, then the quality factor after this change will be--------.
As we know that Q =
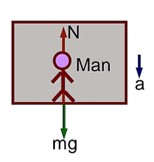
A person standing on a balance inside a stationary lift measures 60 kg. The weight of that person if the lift descends with uniform downward acceleration of 1.8m/s2 will be----------N. [g = 10 m/s2]
mg – N = ma
N = m (g – a) = 60 * (10 – 1.8) = 60 * 8.2 = 492 N
A radiation is emitted by 1000W bulb and it generates an electric field and magnetic field at P, placed at a distance of 2m.Th efficiency of the bulb is 1.25%. The value of peak electric field at P is x × 10-1 V/m. Value of x is----------. (Rounded – off to the nearest integer)
[Take
Here is the efficiency
The mass per unit length of a uniform wire is 0.135 g/cm. A transverse wave of the form y = -0.21 sin(x + 30t) is produced in it, where x is in meter and t is in second. Then, the expected value of tension in the wire is x × 10-2 N. Value of x is-----------. (Round-off to the nearest integer)
JEE Mains 2020
JEE Mains 2020
Physics NCERT Exemplar Solutions Class 11th Chapter Ten Exam