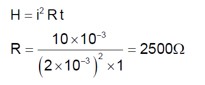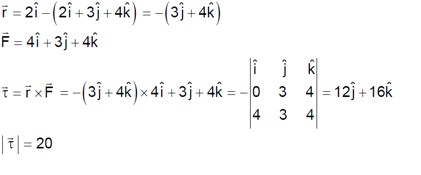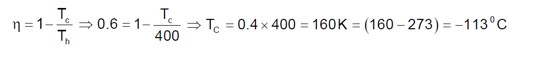A conducting bar of length L is free to slide on two parallel conducting rails as shown in the figure. Two resistors R1 and R2 are connected across the ends of the rails. There is a uniform magnetic field pointing into the page. An external agent pulls the bar to the left at a constant speed v. The correct statement about the directions of induced currents I1 and I2 flowing through R1 and R2 respectively is:

I 1 is in anticlockwise direction and I 2 is in clockwise direction

Both I 1 and I 2 are in anticlockwise direction

Both I 1 and I 2 are in clockwise direction

I 1 is in clockwise direction and I 2 is in anticlockwise direction

The angle of deviation through a prism is minimum when (A) Incident ray and emergent ray are symmetric to the prism (B) The refracted ray inside the prism becomes parallel to its base (C) Angle if incidence is equal to that of the angle of emergence (D) When angle of emergence is double the angle of incidence Choose the correct answer from the options given below :

Only statements (A) and (B) are true

Statements (B) and (C) are true

In thermodynamics, heat and work are :

Intensive thermodynamic state variables

Extensive thermodynamic state variables

Physics NCERT Exemplar Solutions Class 11th Chapter Twelve: Overview, Questions, Preparation

Updated on Apr 24, 2025 12:04 IST

By Raj Pandey

Table of content

Thermodynamics Questions and Answers

Thermodynamics Questions and Answers

1. Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in Fig.

Explanation- pV^1/2= constant

P=k/ $\sqrt[]{V}$

Work done from 1 to 2

W= $\int_{V 1}^{V 2} p d V = K \int_{V 1}^{V 2} \frac{d V}{\sqrt[]{V}} = k {[\frac{\sqrt[]{V}}{\frac{1}{2}}]}_{V 1}^{V 2} = 2 K (\sqrt[]{V_{2}} - \sqrt[]{V_{1}})$

from ideal equation = pV=nRT

T= pV/nR= $\frac{p \sqrt[]{V} \sqrt[]{V}}{n R}$

T= $\frac{K \sqrt[]{V}}{n R}$

T₁= $\frac{K \sqrt[]{V 1}}{n R}$ , T₁= $\frac{K \sqrt[]{V 2}}{n R}$

$\frac{T_{1}}{T_{2}} = \frac{\frac{k \sqrt[]{V_{1}}}{n R}}{\frac{k \sqrt[]{V_{2}}}{n R}} = {\sqrt[]{\frac{V_{1}}{V_{2}}}}^{}$ = $\sqrt[]{\frac{V_{1}}{2 V_{1}}} = \frac{1}{\sqrt[]{2}}$

U= $\frac{3}{2} R T$

$∆ U = U_{2} - U_{1} = \frac{3}{2} R (T_{1} - T_{2})$

= $\frac{3}{2}$ RT₁( $\sqrt[]{V} - 1$ )

$∆ W$ =2p₁V₁^1/2( $\sqrt[]{V_{2}} - \sqrt[]{V_{2}}$ )

= 2p₁V₁^1/2(2 $\sqrt[]{V_{1}} - \sqrt[]{V_{1}}$ )

= 2p₁V₁( $\sqrt[]{2} - 1$ )= 2RT₁( $\sqrt[]{2} - 1$ )

$∆ Q$ = $∆ U + ∆ W$

= $\frac{3}{2}$ RT₁( $\sqrt[]{2} - 1$ )+ 2RT₁( $\sqrt[]{2} - 1$ )

= $\frac{7}{2} R T_{1} (\sqrt[]{2} - 1)$

2. A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in Fig .

A to B : volume constant B to C : adiabatic C to D : volume constant D to A : adiabatic V_c=V_D=2V_A=2V_B

(a) In which part of the cycle heat is supplied to the engine from outside?

(b) In which part of the cycle heat is being given to the surrounding by the engine?

(c) What is the work done by the engine in one cycle? Write your answer in term of PA, PB, VA.

(d) What is the efficiency of the engine? [γ =5/3 for the gas], (C_v= 3/2R for one mole)

Explanation-a) for the process AB

dV=0 and dW=0

dQ=dU+dW=dU

dQ=dU= change in internal energy , so heat utilised is equal to change in internal energy.

Since p= $\frac{n R}{V} T,$ in adiabatic temperature is directly proportional to pressure. So heat is supplied to the system in process AB.

b) for the process CD volume is constant but the pressure decreases, hence temperature also decreases . so heat is also given to the surroundings.

c) W_AB= $\int_{A}^{B} p d V = 0$ , W_CD= $\int_{V c}^{V d} p d V = 0$

W_BC= $\int_{V B}^{V c} p d V = k \int_{V B}^{V c} \frac{d V}{V^{Y}} = \frac{k}{1 - Y} [V^{1 - Y}]$

= $\frac{1}{1 - Y}$ [pV]= $\frac{P_{c} V_{c} - P_{B} V_{B}}{1 - Y}$

W_DA= $\frac{P_{A} V_{A} - P_{D} V_{D}}{1 - Y}$

B and C lies on adiabatic curve BC

P_BV_B^Y= P_CV_C^Y

P_C = P_B( $\frac{V_{B}}{V_{C}}$ )^Y = P_B( $\frac{1}{2}$ )^Y= 2^-YP_B

Total work done by the engine in one cycle ABCDA

W= W_AB+W_BC+W_CD+W_DA= W_BC+W_DA

= $\frac{P_{C} V_{C} - P_{B} V_{B}}{1 - Y} + \frac{P_{A} V_{A} - P_{D} V_{D}}{1 - Y}$

W = $\frac{1}{1 - Y} [2^{- Y} P_{B} 2 V_{B} - P_{B} V_{B} + P_{A} P_{A} - 2^{- Y} P_{B} 2 V_{B}]$

W = $\frac{1}{1 - Y} (2^{1 - Y} - 1) (P_{B} - P_{A}) V_{A}$

W= $\frac{3}{2} [1 - (\frac{1}{2})$ ^2/3]( $P_{B} - P_{A}$ )V_A

3. A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in Fig.. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2) R)

Explanation-a) for process AB

Volume is constant , hence work done dW=0

dQ=dU+dW=dU+0=dU

= nC_vdT= nC_v(T_B-T_A)

= $\frac{3}{2} R (T_{B} - T_{A})$

= $\frac{3}{2} (R T_{B} - R T_{A}) = \frac{3}{2} (P_{B} V_{B} - P_{A} V_{A})$

Heat exchanged = $\frac{3}{2} (P_{B} V_{B} - P_{A} V_{A})$

b) for process BC , p =constant

dQ= dU+dW = $\frac{3}{2} R (T_{C} - T_{B}) + P_{B} (V_{C} - V_{B})$

heat exchanged = $\frac{5}{2} P_{B} (V_{C} {- V}_{A})$

c) for process CD , because CD is adiabatic , dQ= heat exchanged =0

d) DA involves compression of gas from V_D to V_A at constant pressure P_A

heat transferred as similar way as BC₁

hence dQ = $\frac{5}{2}$ P_A(V_A-V_D)

4. Consider that an ideal gas (n moles) is expanding in a process given by P = f ( V ), which passes through a point (P_o, V₀ ). Show that the gas is absorbing heat at (P₀, V_o ) if the slope of the curve P = f (V ) is larger than the slope of the adiabat passing through (P_o, V₀ ).

Explanation- slope of the curve = f(V) , where V is the volume

Slope of P = f(V) curve at ((P_o, V₀ )= f(V_o)

Slope of adiabatic at (P_o, V₀ )= k(-Y)V_o^-1-Y =-YP_o/V_o

Now heat absorbed in the process P= f(V)

dQ=dU+dW= nC_vdT+pdV

pV=nRT

T= pV/nR

T= $\frac{1}{n R} [f (V) + V f^{'} (V) d V]$

$\frac{d Q}{d V} =$ nC_{v
$\frac{d T}{d V} + p \frac{d V}{d V} = n C_{V} \frac{d T}{d V} + P$}

$\frac{C_{V}}{R} [f (V_{o} + V_{0} f^{'} (V) + f (V)]$

After solving we get

${[\frac{d Q}{d V}]}_{v = v o} =$ $[\frac{1}{Y - 1} + 1] f (V_{o}) + \frac{V_{o} f^{' V_{o}}}{Y - 1}$

= $\frac{Y}{Y - 1} P_{o} + \frac{V_{o}}{Y - 1} f^{'} (V_{o})$

Heat is absorbed where dQ/dV>0 when gas expands

Hence YP_o+V_of’(V_o)>0 or f’(V_o)>(-Y $\frac{P_{o}}{V_{o}}$ )

Commonly asked questions

Consider a P-V diagram in which the path followed by one mole of perfect gas in a cylindrical container is shown in Fig.

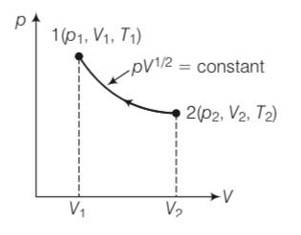
(a) Find the work done when the gas is taken from state 1 to state 2.

(b) What is the ratio of temperature T₁/T₂, if V₂ = 2V₁?

(c) Given the internal energy for one mole of gas at temperature T is (3/2) RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V₂ = 2V₁.

This is a long answer type question as classified in NCERT Exemplar

pV^1/2= constant

P=k/ $\sqrt[]{V}$

Work done from 1 to 2

W= $\int_{V 1}^{V 2} p d V = K \int_{V 1}^{V 2} \frac{d V}{\sqrt[]{V}} = k {[\frac{\sqrt[]{V}}{\frac{1}{2}}]}_{V 1}^{V 2} = 2 K (\sqrt[]{V_{2}} - \sqrt[]{V_{1}})$

from ideal equation = pV=nRT

T= pV/nR= $\frac{p \sqrt[]{V} \sqrt[]{V}}{n R}$

T= $\frac{K \sqrt[]{V}}{n R}$

T₁= $\frac{K \sqrt[]{V 1}}{n R}$ , T₁= $\frac{K \sqrt[]{V 2}}{n R}$

$\frac{T_{1}}{T_{2}} = \frac{\frac{k \sqrt[]{V_{1}}}{n R}}{\frac{k \sqrt[]{V_{2}}}{n R}} = {\sqrt[]{\frac{V_{1}}{V_{2}}}}^{}$ = $\sqrt[]{\frac{V_{1}}{2 V_{1}}} = \frac{1}{\sqrt[]{2}}$

U= $\frac{3}{2} R T$

$? U = U_{2} - U_{1} = \frac{3}{2} R (T_{1} - T_{2})$

= $\frac{3}{2}$ RT₁( $\sqrt[]{V} - 1$ )

$? W$ =2p₁V₁^1/2( $\sqrt[]{V_{2}} - \sqrt[]{V_{2}}$ )

= 2p₁V₁^1/2(2 $\sqrt[]{V_{1}} - \sqrt[]{V_{1}}$ )

= 2p₁V₁( $\sqrt[]{2} - 1$ )= 2RT₁( $\sqrt[]{2} - 1$ )

$? Q$ = $? U + ? W$

= $\frac{3}{2}$ RT₁( $\sqrt[]{2} - 1$ )+ 2RT₁( $\sqrt[]{2} - 1$ )

= $\frac{7}{2} R T_{1} (\sqrt[]{2} - 1)$

A cycle followed by an engine (made of one mole of perfect gas in a cylinder with a piston) is shown in Fig .

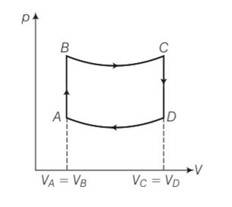
A to B : volume constant B to C : adiabatic C to D : volume constant D to A : adiabatic V_c=V_D=2V_A=2V_B

(a) In which part of the cycle heat is supplied to the engine from outside?

(b) In which part of the cycle heat is being given to the surrounding by the engine?

(c) What is the work done by the engine in one cycle? Write your answer in term of P_A, P_B, V_A

(d) What is the efficiency of the engine? [γ =5/3 for the gas], (C_v= 3/2R for one mole)

This is a long answer type question as classified in NCERT Exemplar

(a) For the process AB

dV=0 and dW=0

dQ=dU+dW=dU

dQ=dU= change in internal energy , so heat utilised is equal to change in internal energy.

Since p= $\frac{n R}{V} T,$ in adiabatic temperature is directly proportional to pressure. So heat is supplied to the system in process AB.

(b) For the process CD volume is constant but the pressure decreases, hence temperature also decreases . so heat is also given to the surroundings.

(c) W_AB= $\int_{A}^{B} p d V = 0$ , W_CD= $\int_{V c}^{V d} p d V = 0$

W_BC= $\int_{V B}^{V c} p d V = k \int_{V B}^{V c} \frac{d V}{V^{Y}} = \frac{k}{1 - Y} [V^{1 - Y}]$

= $\frac{1}{1 - Y}$ [pV]= $\frac{P_{c} V_{c} - P_{B} V_{B}}{1 - Y}$

W_DA= $\frac{P_{A} V_{A} - P_{D} V_{D}}{1 - Y}$

B and C lies on adiabatic curve BC

P_BV_B^Y= P_CV_C^Y

P_C = P_B( $\frac{V_{B}}{V_{C}}$ )^Y = P_B( $\frac{1}{2}$ )^Y= 2^-YP_B

Total work done by the engine in one cycle ABCDA

W= W_AB+W_BC+W_CD+W_DA= W_BC+W_DA

= $\frac{P_{C} V_{C} - P_{B} V_{B}}{1 - Y} + \frac{P_{A} V_{A} - P_{D} V_{D}}{1 - Y}$

W = $\frac{1}{1 - Y} [2^{- Y} P_{B} 2 V_{B} - P_{B} V_{B} + P_{A} P_{A} - 2^{- Y} P_{B} 2 V_{B}]$

W = $\frac{1}{1 - Y} (2^{1 - Y} - 1) (P_{B} - P_{A}) V_{A}$

W= $\frac{3}{2} [1 - (\frac{1}{2})$ ^2/3]( $P_{B} - P_{A}$ )V_A

A cycle followed by an engine (made of one mole of an ideal gas in a cylinder with a piston) is shown in Fig.. Find heat exchanged by the engine, with the surroundings for each section of the cycle. (Cv = (3/2) R)

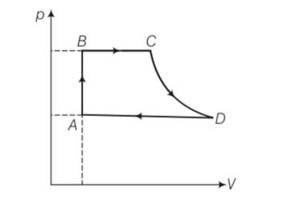
AB : constant volume

BC : constant pressure

CD : adiabatic

DA : constant pressure

This is a long answer type question as classified in NCERT Exemplar

(a) For process AB

Volume is constant , hence work done dW=0

dQ=dU+dW=dU+0=dU

= nC_vdT= nC_v(T_B-T_A)

= $\frac{3}{2} R (T_{B} - T_{A})$

= $\frac{3}{2} (R T_{B} - R T_{A}) = \frac{3}{2} (P_{B} V_{B} - P_{A} V_{A})$

Heat exchanged = $\frac{3}{2} (P_{B} V_{B} - P_{A} V_{A})$

(b) For process BC , p =constant

dQ= dU+dW = $\frac{3}{2} R (T_{C} - T_{B}) + P_{B} (V_{C} - V_{B})$

heat exchanged = $\frac{5}{2} P_{B} (V_{C} {- V}_{A})$

(c) For process CD , because CD is adiabatic , dQ= heat exchanged =0

(d) DA involves compression of gas from V_D to V_A at constant pressure P_A

heat transferred as similar way as BC₁

hence dQ = $\frac{5}{2}$ P_A(V_A-V_D)

Consider that an ideal gas (n moles) is expanding in a process given by P = f ( V ), which passes through a point (P_o, V₀ ). Show that the gas is absorbing heat at (P₀, V_o ) if the slope of the curve P = f (V ) is larger than the slope of the adiabat passing through (P_o, V₀ ).

This is a long answer type question as classified in NCERT Exemplar

Slope of the curve = f(V) , where V is the volume

Slope of P = f(V) curve at ((P_o, V₀ )= f(V_o)

Slope of adiabatic at (P_o, V₀ )= k(-Y)V_o^-1-Y =-YP_o/V_o

Now heat absorbed in the process P= f(V)

dQ=dU+dW= nC_vdT+pdV

pV=nRT

T= pV/nR

T= $\frac{1}{n R} [f (V) + V f^{'} (V) d V]$

$\frac{d Q}{d V} =$ nC_{v $\frac{d T}{d V} + p \frac{d V}{d V} = n C_{V} \frac{d T}{d V} + P$}

$\frac{C_{V}}{R} [f (V_{o} + V_{0} f^{'} (V) + f (V)]$

After solving we get

${[\frac{d Q}{d V}]}_{v = v o} =$ $[\frac{1}{Y - 1} + 1] f (V_{o}) + \frac{V_{o} f^{' V_{o}}}{Y - 1}$

= $\frac{Y}{Y - 1} P_{o} + \frac{V_{o}}{Y - 1} f^{'} (V_{o})$

Heat is absorbed where dQ/dV>0 when gas expands

Hence YP_o+V_of’(V_o)>0 or f’(V_o)>(-Y $\frac{P_{o}}{V_{o}}$ )

Consider one mole of perfect gas in a cylinder of unit cross section with a piston attached . A spring (spring constant k) is attached (unstretched length L ) to the piston and to the bottom of the cylinder. Initially the spring is unstretched and the gas is in equilibrium. A certain amount of heat Q is supplied to the gas causing an increase of volume from V_o to V₁.

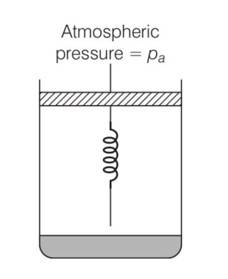
(a) What is the initial pressure of the system?

(b) What is the final pressure of the system?

(c) Using the first law of thermodynamics, write down a relation between Q, Pa, V, Vo and k.

This is a long answer type question as classified in NCERT Exemplar

(a) Initially the piston is in equilibrium P_i=P_a

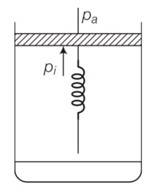
(b) On supplying heat , the gas expands from V_o to V_i

so increase in volume of the gas =V_i-V_o

as the piston is of unit cross sectional area hence extension in the spring

x= $\frac{V_{i} - V_{0}}{a r e a} = V_{i} - V_{0}$

force exerted by the spring on the piston= F= kx= K(V_i- V_o)

hence final pressure =P_f =P_a +kx

= P_a+K $\times$ ( $V_{i} - V_{0}$ )

(c) From first law of thermodynamics

dQ=dU+dW

dU=C_v(T-T_o) = C_v(T-T_o)

T= $\frac{P_{f} V_{1}}{R} = [\frac{P_{a} + K (V_{i} - V_{0})}{R}] \frac{V_{1}}{R}$

Work done by the gas =pdV+ increase in PE of the spring

= P_a(V₁-V_o) + $\frac{1}{2} k$ x²

dQ=dU+dW

= C_v(T-T_o)+P_a(V-V_o)+ $\frac{1}{2} k$ x²

= C_v(T-T_o)+P_a(v-V_o)+1/2 ( $V_{i} - V_{0}$ )²

Can a system be heated and its temperature remains constant?

This is a short answer type question as classified in NCERT Exemplar

Yes this is possible when the entire heat supplied to the system is utilised in expansion.

So its working against the surroundings.

A system goes from P to Q by two different paths in the P-V diagram as shown in Fig. 12.8. Heat given to the system in path 1 is 1000 J. The work done by the system along path 1 is more than path 2 by 100 J. What is the heat exchanged by the system in path 2?

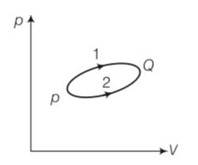
This is a short answer type question as classified in NCERT Exemplar

For path1

Heat Q₁= 1000J

Work done =W₁

For path 2

Work done W₂= W₁-100

As change in internal energy is same

dU=Q₁-W₁=Q₂-W₂

1000-W₁=Q₂-W₁+100

Q₂= 1000-100= 900J

If a refrigerator’s door is kept open, will the room become cool or hot? Explain.

This is a short answer type question as classified in NCERT Exemplar

If a refrigerator's doors is kept open, then room will become hot, because amount of heat removed would be less than the amount of heat released in the room.

Is it possible to increase the temperature of a gas without adding heat to it? Explain.

This is a short answer type question as classified in NCERT Exemplar

Yes during adiabatic compression the temperature of a gas increases while no heat is

In adiabatic compression dQ=0

From the first law of thermodynamics dU= dQ-dW

dU=-dW

in compression work is done on the gas i.e work done is negative

dU=positive

hence internal energy of the gas increases due to which its temperature increases.

Air pressure in a car tyre increases during driving. Explain.

This is a short answer type question as classified in NCERT Exemplar

During driving temperature of the gas increases while volume remains constant. So according charle's law, at constant volume V.

Pressure is directly proportional to temperature. Therefore pressure of gas increases.

Consider a Carnot’s cycle operating between T₁= 500K and T₂=300K producing 1 k J of mechanical work per cycle. Find the heat transferred to the engine by the reservoirs.

This is a short answer type question as classified in NCERT Exemplar

Temperature of the source T₁= 500K and sink T₂= 300K

Work done W= 1000J

Efficiency of Carnot engine = 1-T₂/T₁= 1-300/500= 200/500= 2/5

Efficiency = W/Q₁

So Q₁= W/efficiency = 1000 $(\frac{5}{2}) = 2500 J$

A person of mass 60 kg wants to lose 5 kg by going up and down a 10m high stairs. Assume he burns twice as much fat while going up than coming down. If 1 kg of fat is burnt on expending 7000 kilo calories, how many times must he go up and down to reduce his weight by 5 kg?

This is a short answer type question as classified in NCERT Exemplar

Height of stairs h= 10m

Energy produced by burning 1 kg of fat = 7000Kcal

Energy produced by burning 5kg of fat = 5 $\times 7000 = 35000 K c a l$

Energy utilised in going up and down one time

= mgh + $\frac{1}{2} m g h$ = $\frac{3}{2} m g h$

= $\frac{3}{2} \times 60 \times 10 \times 10$

= 9000J= 9000/4.2=3000/1.4cal

Number of times, the person has to go up and down the stairs

= $\frac{35 \times 10^{6}}{\frac{3000}{1.4}} = \frac{3.5 \times 1.4 \times 10^{6}}{3000}$ = 16.3 $\times 10^{3}$ times

Consider a cycle tyre being filled with air by a pump. Let V be the volume of the tyre (fixed) and at each stroke of the pump ?V V ( ) of air is transferred to the tube adiabatically. What is the work done when the pressure in the tube is increased from P₁ to P₂?

This is a short answer type question as classified in NCERT Exemplar

For adiabatic change process we know

P₁V₁^y= P₂V₂^y

P (V+ $? V$ )^y = (P+ $? P$ )V^y

PV^y (1+ $\frac{? V}{V}$ ) ^y=p (1+ $\frac{? P}{P}$ )V^y

PV^y (1+ $\frac{? V}{V}$ ) $\approx$ PV^y (1+ $\frac{? V}{V}$ )

Y $\frac{? V}{V} = \frac{? P}{P}$

dV= $\frac{1}{Y} \frac{V}{p} d P$

hence work done increasing the pressure from P₁ to P₂

W= $\int_{p 1}^{p 2} p d V = \int_{p 2}^{p 1} p \frac{1}{Y} \frac{V}{p} d p$

= $\frac{V}{Y} (P_{2} - P_{1})$

W= $\frac{P_{2} - P_{1}}{Y} V$

In a refrigerator one removes heat from a lower temperature and deposits to the surroundings at a higher temperature. In this process, mechanical work has to be done, which is provided by an electric motor. If the motor is of 1kW power, and heat is transferred from –3°C to 27°C, find the heat taken out of the refrigerator per second assuming its efficiency is 50% of a perfect engine.

This is a short answer type question as classified in NCERT Exemplar

Temperature of the source is 27⁰C

T₁= 27+273= 300K

T₂= -3+273= 270K

Efficiency of heat engine = 1-T₂/T₁= 1-270/300=1/10

Efficiency of refrigerator is 50% of a perfect engine

= 0.5 $\times η$ = 1/20

Coefficient of performance of the refrigerator $β = \frac{Q_{2}}{W} = \frac{1 - η^{'}}{η}$

= $\frac{1 - 1 / 20}{1 / 20} = \frac{19 / 20}{1 / 20} = 19$

Q₂= $β W$ =19W

= 19 $\times$ 1KW=19KW= 19kJ/s

If the co-efficient of performance of a refrigerator is 5 and operates at the room temperature (27 °C), find the temperature inside the refrigerator.

This is a short answer type question as classified in NCERT Exemplar

Coefficient of $β = 5$

T₁= 27+273=300K

Coefficient of performance $β = \frac{T_{2}}{300 - T_{2}}$

1500-5T₂=T₂

6T₂=1500

T₂= 250K

T₂= 250-273=-23^oC

The initial state of a certain gas is (Pi , Vi , Ti ). It undergoes expansion till its volume becomes V_f . Consider the following two cases:

(a) The expansion takes place at constant temperature.

(b) The expansion takes place at constant pressure. Plot the P-V diagram for each case. In which of the two cases, is the work done by the gas more?

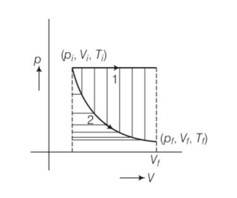
This is a short answer type question as classified in NCERT Exemplar

process 1 isochoric and process 2 is isothermal .

Since, work done = area under P-V curve . here area under the pV curve 1 is more . so work done is more when the gas expands in isochoric process.

An ideal gas undergoes four different processes from the same initial state (Fig. 12.1). Four processes are adiabatic, isothermal, isobaric and isochoric. Out of 1, 2, 3 and 4 which one is adiabatic.

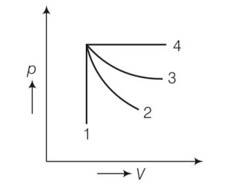
(a) 4

(b) 3

(c) 2

(d) 1

This is a multiple choice answer as classified in NCERT Exemplar

(c) For the curve 1 volume is constant so it is isochoric process. But in curve 2 and 3 curve 2 is steeper so 2 is adiabatic and 3 is isothermal.

If an average person jogs, he produces 14.5 × 10³ cal/min. This is removed by the evaporation of sweat. The amount of sweat evaporated per minute (assuming 1 kg requires 580 × 10³ cal for evaporation) is

(a) 0.25 kg

(b) 2.25 kg

(c) 0.05 kg

(d) 0.20 kg

This is a multiple choice answer as classified in NCERT Exemplar

(a) Amount of sweat evaporated /minute = $\frac{\frac{s w e a t p r o d u c e d}{m i n u t e}}{n u m b e r o f c a l o r i e s r e q u i r e d f o r e v a p o r a t i o n \frac{}{k g}}$

= $\frac{14.5 \times 10^{3}}{580 \times 10^{3}} = 0.25 k g$

Consider P-V diagram for an ideal gas shown in Out of the following diagrams , which represents the T-P diagram?

This is a multiple choice answer as classified in NCERT Exemplar

Hence we can say that gas is going through an isothermal process.

Clearly from the graph that between process 1 and 2 temperature is constant and the gas expands and pressure decreases. So density of 2 is less than 1 so option ii

An ideal gas undergoes cyclic process ABCDA as shown in given P-V diagram (Fig. 12.4). The amount of work done by the gas is

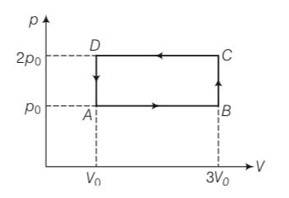
(a) 6 P_oV_o

(b) –2 P_oV_o

(c) + 2 P_oV_o

(d) + 4 P_oV_o

This is a multiple choice answer as classified in NCERT Exemplar

(b) Work done ABCD = area of rectangle ABCDA

= AB $\times B C$ = (3V_o-V_o) $\times$ (2p_o-p_o)

= 2V_{0 $\times$}P_o= 2p_oV_o

And work done by the gas =- 2p_oV_o

Consider two containers A and B containing identical gases at the same pressure, volume and temperature. The gas in container A is compressed to half of its original volume isothermally while the gas in container B is compressed to half of its original value adiabatically. The ratio of final pressure of gas in B to that of gas in A is

(a) $2^{γ - 1}$

(b) ${(\frac{1}{2})}^{γ - 1}$

(c) $({\frac{1}{1 - γ})}^{2}$

(d) ${(\frac{1}{γ - 1})}^{2}$

This is a multiple choice answer as classified in NCERT Exemplar

(a) Container A is isothermal and container B is adiabatic

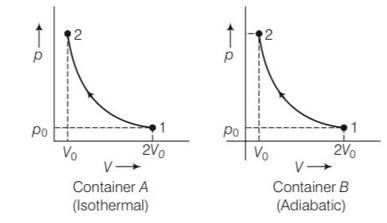
For isothermal process P₁V₁=P₂V₂

P_o (2V_o)= P₂ (V_o)

P₂= 2P_o

for adiabatic process

P₁V₁^y= P₂V₂^y

P_o (2V_o)^y=P₂ (V_o)^y

P₂= ( $\frac{2 V_{o}}{V_{o}}$ )^yP_o= 2^yP_o

Hence ratio of final pressure = $\frac{2^{γ} P_{o}}{2 P_{o}} = 2^{γ - 1}$

Three copper blocks of masses M₁, M₂ and M₃ kg respectively are brought into thermal contact till they reach equilibrium. Before contact, they were at T₁, T₂, T₃ (T₁ > T₂ > T₃). Assuming there is no heat loss to the surroundings, the equilibrium temperature T is (s is specific heat of copper)

(a) T= $\frac{T_{1} + T_{2} + T_{3}}{3}$

(b) T= $\frac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{M_{1} + M_{2} + M_{3}}$

(c) T= $\frac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{3 (M_{1} + M_{2} + M_{3})}$

(d) T= $\frac{M_{1} T_{1} s + M_{2} T_{2} s + M_{3} T_{3} s}{M_{1} + M_{2} + M_{3}}$

This is a multiple choice answer as classified in NCERT Exemplar

(b) Let us assume that T₁, T₂T₃

According to questions there is no loss of heat in the surroundings

Heat lost by M₃ = heat gained by M₁+ heat gained by M₂

M₃s (T₃-T)= M₁s (T-T₁)+M₂s (T-T₂)

T [M₁+M₂+M₃]= M₃T₃+M₁T₁+M₂T₂

T = $\frac{M_{1} T_{1} + M_{2} T_{2} + M_{3} T_{3}}{M_{1} + M_{2} + M_{3}}$

Which of the processes described below are irreversible?

(a) The increase in temperature of an iron rod by hammering it

(b) A gas in a small container at a temperature T₁ is brought in contact with a big reservoir at a higher temperature T₂ which increases the temperature of the gas

(c) A quasi-static isothermal expansion of an ideal gas in cylinder fitted with a frictionless piston

(d) An ideal gas is enclosed in a piston cylinder arrangement with adiabatic walls. A weight W is added to the piston, resulting in compression of gas

This is a multiple choice answer as classified in NCERT Exemplar

(a), (b), (d) When the rod is hammered the external work is done on the rod which increases its temperature.

Heat is transferred to the gas in the small container by big reservoir at temperature T₂

As the weight is added to the cylinder arrangement in the form of external pressure so it cannot reversed.

An ideal gas undergoes isothermal process from some initial state i to final state f. Choose the correct alternatives.

(a) dU = 0

(b) dQ= 0

(c) dQ = dU

(d) dQ = dW

This is a multiple choice answer as classified in NCERT Exemplar

(a), (d) For isothermal dT= 0 so T=constant

For an ideal gas dU = change in internal energy = nC_vdT=0

From first law of thermodynamics dQ= dU+dW

dQ= dW

Figure 12.5 shows the P-V diagram of an ideal gas undergoing a change of state from A to B. Four different parts I, II, III and IV as shown in the figure may lead to the same change of state.

(a) Change in internal energy is same in IV and III cases, but not in I and II

(b) Change in internal energy is same in all the four cases

(c) Work done is maximum in case I

(d) Work done is minimum in case II

This is a multiple choice answer as classified in NCERT Exemplar

(b), (c) Change in internal energy for process A to B

dU=nC_vdT=nC_v (dT)=nC_v (T_B-T_A)

work done from A to B = area under the PV curve which is maximum for path I

Consider a cycle followed by an engine 1 to 2 is isothermal 2 to 3 is adiabatic 3 to 1 is adiabatic Such a process does not exist because

(a) Heat is completely converted to mechanical energy in such a process, which is not possible.

(b) Mechanical energy is completely converted to heat in this process, which is not possible.

(c) Curves representing two adiabatic processes don’t intersect.

(d) Curves representing an adiabatic process and an isothermal process don’t intersect.

This is a multiple choice answer as classified in NCERT Exemplar

(a) the given process is a cyclic process i.e returns to the original state 1

Hence change in internal energy dU =0

dQ= dU+dW=0+dW

hence total heat supplied is converted to work done by the gas which is not possible by second law of thermodynamics.

(c) When the gas expands adiabatically from 2 to 3 . it is not possible to return to the same state without being heat supplied hence 3 to 1 cannot be adiabatic.

Consider a heat engine as shown in Fig. Q₁and Q₂ are heat added to heat bath T₁ and heat taken from T₂ in one cycle of engine. W is the mechanical work done on the engine. If W > 0, then possibilities are:

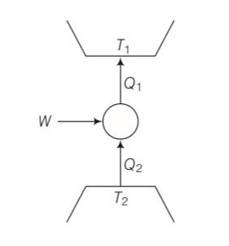
(a) Q₁> Q₂> 0

(b) Q₂ > Q₁ > 0

(c) Q₂ < Q₁ < 0

(d) Q₁ < 0, Q₂ > 0

This is a multiple choice answer as classified in NCERT Exemplar

(a), (c) Q₁= W+Q₂

W=Q₁-Q₂>0

Q₁>Q₂>0

We can also write Q₂1

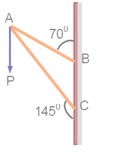
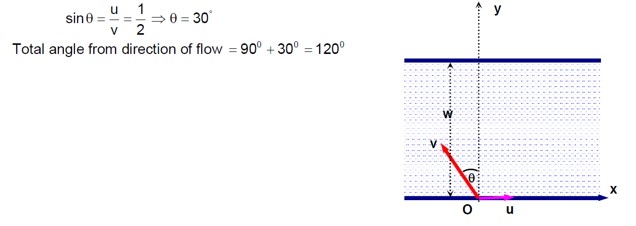
Consider a frame that is made up of two thin massless rods AB and AC as shown in the figure. A vertical force $\overset{?}{P}$ of magnitude 100N is applied at point A of the frame. Suppose the force is $\overset{?}{P}$ resolved parallel to the arms AB and AC of the frame. The magnitude of the resolved component along the arm AC is xN. The value of x, to the nearest integer, is------------. [Given : sin(35° ) = 0.573, cos(35° )= 0.819 sin(110° )= 0.939, cos(110° )= -0.342 ]

Kindly consider the following Image

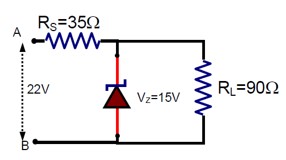
The value of power dissipated across the Zener diode ( Vz = 15V) connected in the circuit as shown in the figure is x x10-1 watt. The value of x, to the nearest integer, is--------.

Kindly consider the following Image

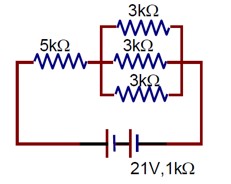
In the figure given, the electric current flowing through the 5 k â„¦ resistor is â€˜xâ€™ mA. The value of x to the nearest integer is --------.

Kindly consider the following Image

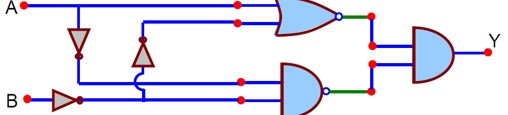
In the logic circuit shown in the figure, if input A and B are 0 to 1 respectively, then output at Y would be â€˜xâ€™.

The value of x is ----------.

Kindly consider the following Image

The resistance R = V/I where V =(50 Â± 2V) and I = (20 Â± 0.2)A. The percentage error in R is â€˜xâ€™ %. The value of â€˜xâ€™ to the nearest integer is ----------.

Kindly consider the following Image

A sinusoidal voltage of peak value 250V is applied to a series LCR circuit, in which R = 8â„¦, L = 24mH andC = 60Î¼F. The value of power dissipated at resonant condition is â€˜xâ€™ kW. The value of x to the nearest integer is-----------.

Kindly consider the following Image

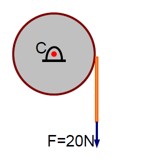
Consider a 20 kg uniform circular disk of radius 0.2 m. It is pin supported at its centre and is at rest initially. The disk is acted upon by a constant force F = 20 N through a massless string wrapped around its periphery as shown in the figure. Suppose the disk makes n number of revolutions to attain an angular speed of 50 rad s-1. The value of n, to the nearest integer, is ---------.

[Given : In one complete revolution, the disk rotates by 6.28 rad ]

Kindly consider the following Image

The first three spectral of H-atom in the Balmer series are given λ₁ , λ₂ , λ₃ considering the Bohr atomic model, the wave lengths of first and third spectral lines (λ₁/ λ₂) are related by a factor of approximately ‘x’ ×10^-1. The value of x, to the nearest integer, is-----------.

Kindly consider the following Image

A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is â€˜xâ€™ nm. The value of â€˜xâ€™ to the nearest integer is----------.

Kindly consider the following Image

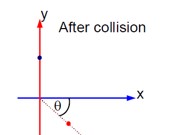
A ball of mass 10 kg moving with a velocity10âˆš3ms-1along X â€“ axis, hits another ball of mass 20 kg which is at rest. After collision, the first ball comes to rest and the second one disintegrates into two equal pieces. One of the pieces starts moving along Yâ€“ axis at a speed of 10m/s. The second piece starts moving at a speed of 20m/s at an angle Î¸Â° with respect to the X â€“axis. The configuration of pieces after collision is shown in the figure. The value of Î¸ to the nearest integer is----------.

Kindly consider the following Image

Physics NCERT Exemplar Solutions Class 11th Chapter Twelve Exam

Student Forum

Anything you would want to ask experts?

Write here...

Other Similar chapters for you

Thermodynamics

News & Updates

Latest NewsPopular News

Physics NCERT Exemplar Solutions Class 11th Chapter Twelve: Overview, Questions, Preparation

Thermodynamics Questions and Answers

Commonly asked questions

Try these practice questions

Student Forum

Other Similar chapters for you

News & Updates

RRB Group D City Intimation 2025 Out, Check Details Here

RRB Group D 2025: Exam Dates (OUT), Admit Card, City Slip, Exam Pattern & Syllabus

ICSI CSEET Result November 2025 at icsi.edu LIVE: Scorecard Direct Link Soon; Pass Percentage

AP 10th Class Public Exam Time Table 2026 shortly @bse.ap.gov.in Live Updates

IBPS Clerk 2025 Prelims Result Download Link (Active Soon) LIVE- Check Expected Cut Off & Updates

JEE Main Marks vs Percentile vs Rank 2025: Calculate Percentile and Rank Using Marks

List of NIT Colleges in India 2025 - NIRF Ranking, Courses, Seats, Cutoff, Fees and Placement

CBSE 10th Maths Question Paper 2025, 2024, 2023, 2022, 2020, 2019 PDF Download

NEET Chapter Wise Weightage 2026 PDF by NTA: Physics, Chemistry & Biology

List of Top IITs in India 2025: NIRF Ranking, Courses, Seats, Fees & Placement